
Pluto and Charon to Earth size comparison
My related essay on cosmology is here: Cosmology
Go to homepage
This essay
is a few select topics from the huge subject of astronomy that I find interesting.
Scale
How
many stars and galaxies in the (visible) universe?
Size
of the solar system distance to near-by stars
Relative
solar system scaling -- sun as a grain of salt
Star
size and spacing
Galaxy
size and spacing
Pluto
and Charon to Earth size comparison
Moon
transists the earth
Neat star scale images
Biggest
stars
Cepheid
luminosity-period relationship --- uncalibrated standard candle
Absolute
cepheid distance --- calibrated standard candle
Age
How old is the universe?
Lifetime of low
mass stars
Globular cluster age
Young
earth evangelical perspective
Stars
H-R diagram
Brown dwarfs
Lithium
in stars
T
Tauri stars -- young stars without fusion
Orion
molecular cloud and Orion's belt stars
Star
formation and dynamics of molecular clouds
Mass of stars
Stellar metallicity
Nearby
halo star -- Kapteyn's Star
Distance to Milky
Way stars
Star winds and mass
loss
Earth
like planets around red dwarf stars
Supernova
Gamma ray bursts
Extraolar
planetary ring system
Galaxy
Milky Way is
a barred spiral
Center of Milky Way
Introduction to
our galaxy
How stars in
a galaxy rotate
Milky Way's large
black hole
Andromeda galaxy
Solar system
Is jupiter a 'failed
star'?
As
bright as the sun -- an amazing jupiter tidbit
Solar
system bodies with (possible) subsurface oceans
Enceladus
and Europa
Venus
Galileo
calculates height of mountains on moon
Liquid on surface
of Titan
Earth's interior
Weighing the earth
Evidence
for a 9th planet beyond the Kuiper Belt
Pluto
and large kuiper belt objects
Solar system formation
Transient of Mercury
Rock from
outside the solar system
Sun
Is the sun an
average star?
What fraction
of the sun is helium?
Where
the hydrogen is
Calculation
of helium created in sun during its lifetime
Original
composition of the sun
Why
do we see the sun as having a surface?
Sun's
internal zones
Sun's
surface or light emitting zone
Sun's
motion
Sun's
fuel burning
Helium
flash
Future
of the sun -- main sequence => red giant => white dwarf/planetary nebulae
Sun's density
and black holes
Black holes
Smallest possible
black hole
Black
hole radius
Black
hole temperature
Black
hole entropy
Black
holes merging captured by a gravity wave observatory
Dynamics
Orbital velocity
calculation
Does
conservation of angular momentum apply?
Subtle
trap?
Orbital
period
L2 lagrangian point
Misc
Early
melting from high radioactivity
Newtonian bending
of starlight
Order
of magnitude calculation
Neutrinos
How Hubble
telescope is pointed
New cosmic
ray observatory (4/27/11)
Galileo
Stoneham HS talk (4/2/09)
Scale
Numbers in astronomy have a way of changing with time, but the estimated number of stars and galaxies in the universe (meaning the fraction of the universe whose light has had time to reach us) is unchanged from 40 years ago when I took astronomy in college. I find this pretty remarkable, considering that the state of the art in astronomy razzle dazzle when my college astronomy 101 textbook was published was a small, slightly fuzzy picture of the galaxy Andromeda.
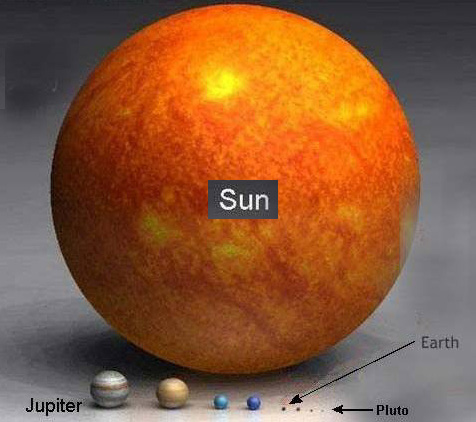
Aside --- The Milky way is larger than average galaxy with 4 x 10^11 stars (400 billion stars). In the local group of 30 galaxies Milk Way is 2nd largest (Andromeda is the largest) and Milky Way has at least 14 satellite galaxies.Size of the solar system distance to near-by stars
body size
earth's diameter
12.8 thousand km
1 earth dia
jupiter's diameter 143 thousand
km
11 earth dia
sun's diameter 1,380
thousand km
108 earth dia, 4.6 light-sec
distance from sun
earth
1 AU (1 astronomical unit), 500 light-sec
jupiter
5.2 AU
pluto
80 AU
Oort cloud 50,000 AU
(comets)
distance to nearby stars
nearest star
4.3 light-years (Alpha Centauri is a triple star system)
2nd nearest star
6 light-years (Barnard's star is a faint, red dwarf)
3rd nearest star
6.5 light-years (WISE 1049-5319 is a very dim, brown dwarf, binary star
system) (discoverd in 2012)
8 light-years (several stars) (prior to 2012)
Relative
solar system scaling -- sun as a grain of salt
Grains of
table salt are really tiny. Looking at some salt from my saltshaker with
my mm scale ruler I find that the linear dimension of a salt cube is about
1/3 mm. If the size of the sun is represented by a salt grain, then the
earth is quite close at 1.4 inches (about 100 sun diameters away) and the
nearest star is distant at 6 miles. Here is the scaling:
sun dia
0.033 cm 4.6 light-sec
sun to earth
3.5 cm 500 light-sec/4.6
light-sec x 0.33 mm
sun to jupiter
18 cm 5.2 AU
x 3.5 cm
sun to pluto
2.8 m
80 AU x 0.035 m
sun to Oort
cloud 1.8 km
50,000 AU x .035 m
sun to alpha
centauri 10 km
2.9 x 10^7 x 0.33 x 10^-3 m (nearest star)
Star size and spacing
The ratio
of star distance to star diameter is about 30 million (ratio of 10 km to
1/3 mm)! This is vastly different from galaxy size and spacing, where
the spacing between galaxies it typically (about) 10 times the dia of galaxies.
On the other hand if we consider the dia of a star system is be its far
out (fuzzy) comet cloud (Oort cloud, named after an astronomer), then the
ratio of star system dia to star spacing is roughly similar to galaxies
(10km/1.8 km = 5).
Galaxy size and
spacing
Galaxy distance
to diameter scaling is hugely different from stars. The large (barred ?)
spiral galaxy we live in (Milky Way) is about 100,000 light years in diameter,
and the nearest similar spiral galaxy (Andromeda) is about 20 dia away
(2 million light years).
(galaxy distance/galaxy dia) = (10 or 20) to 1
There are closer galaxies, in fact the Milky Way has at least 14 known satellite galaxies. Many of these dwarf, satellite galaxies have been found only recently (latest in 2005). Some are hard to see because they are on the opposite side of the galaxy from us and are obscured by dust in the disk. The largest of the satellite galaxies, the large and small Magellanic clouds (160,000 to 200,000 light-years away), can only be seen from the southern hemisphere. They were named for Magellan, who observed them in his circumnavigation of the earth. The large Magellanic cloud has a few per cent of the stars of the Milk Way, but is still the fourth largest galaxy in the local group of 30 galaxies.
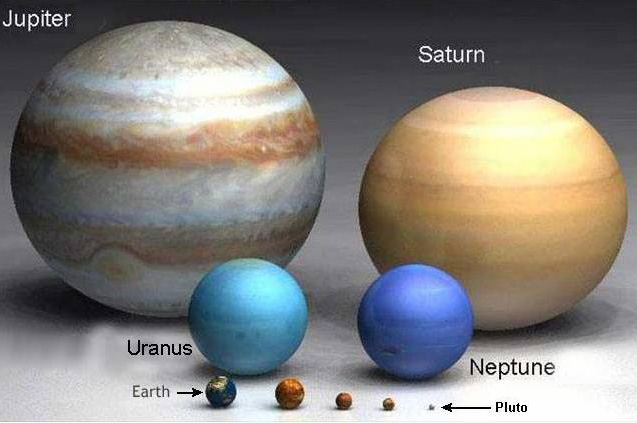
Pluto
and Charon to Earth size comparison (7/13/15)
NASA's New
Horizon's spacecraft has just taken the first close up pictures of pluto
and charon its largest moon. I found this cool size comparison of them
to the size of the earth on the New Horizons web site. This image also
shows some of the (real) surface detail of pluto.

Pluto and Charon to Earth size comparison
Moon transists
the earth
While it looks
like a photoshoped composite, it is not. Taken from NASA's 'Deep Space
Climate Observatory' a million miles from earth it shows the back side
of the moon as the moon passes between earth and the observatory.

moon transits earth as seen from NASA's Deep Space
Climate Observatory 1 million miles out
(source -- http://wordlesstech.com/wp-content/uploads/2015/08/Unique-view-of-Moon-Transiting-the-Earth-1.jpg)
Neat star scale
images
The star scale
images are really interesting, because they so clearly show the huge stellar
size range.
I took the NYC museum photo (below), all the other images from -- http://www.meta-synthesis.com/webbook/32_n-synth/nucleosynthesis.html
Planets to the right of earth: Venus, Mars, Mercury,
Pluto
..

NYC Museum of Natural History (l to r) Mercury, Venus,
Earth, Mars to Sun (sphere in back), all to scale
Larger planets (not shown) hang from ceiling (Fulton
photo)
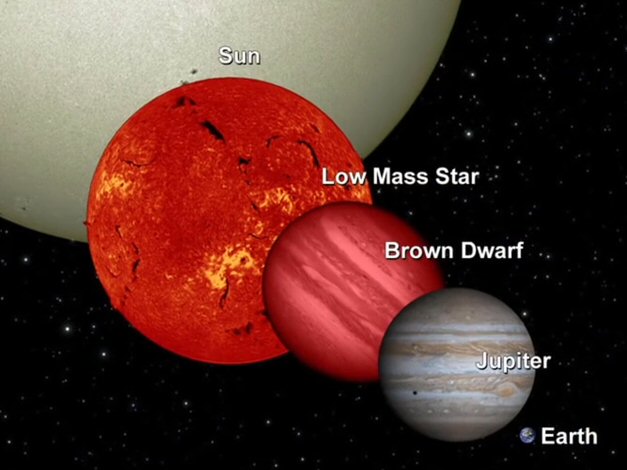
brown dwarfs (no hydrogen fusion) have high density,
so even a (hydrogen) brown dwarf x50 heavier than
jupiter is only a little larger than jupiter
(source --- scn capture from Slate astronomy series
on Brown Dwarfs)

Arcturus is a nearby (37 ly) red giant (helium burning)
star. Its mass is roughly comparable to our sun, so one day our sun will
be this size. Arcturus is 3rd brightest star in the sky.
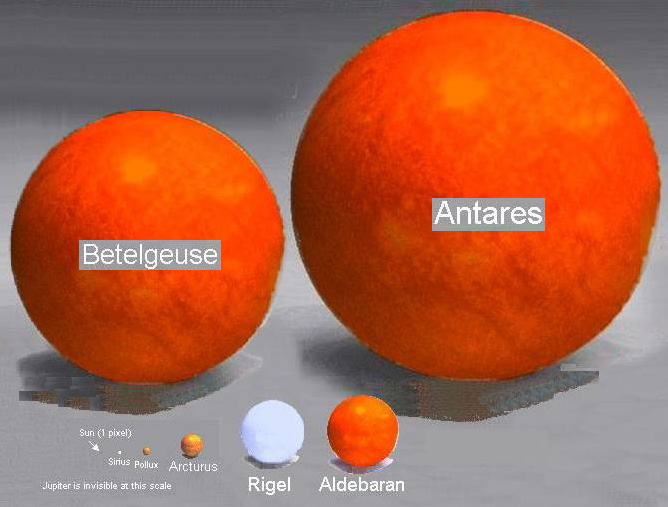
The large stars above are supergiant stars. Antares
and Betelgeuse are red (class M) supergiant stars and Rigel is a blue-white
supergiant.
These stars are all relatively close to us: Antares
is 600 ly, Betelgeuse 430 ly and Rigel 800 ly.
Biggest stars
Antares, a
red supergiant star, (biggest star in the figure above) appears to be the
largest known star in terms of diameter, which is surprising because
it is so close (600 ly), or is it that we can't accurately figure the diameter
of stars far away? Its radius on Wikipedia is shown as 700 solar
radius. To give you an idea of how large this is: The distance from
earth to sun is equal 107 sun diameters = (93 mil mile/0.87 mil mile),
which is 214 sun radiuses. Antares is 700 x sun's radius, which means it
would fill the solar system out beyond the Asteroid belt between Mars and
Jupiter.
"Antares is a class M (M1.5) red supergiant... Its great distance of 600 light years reveals that it is truly luminous, to the eye over 10,000 times brighter than the Sun. Because it is cool, only about 3,600 degrees Kelvin at its surface, it radiates a considerable amount of its light in the invisible infrared. When that is taken into account, the star becomes some 60,000 times brighter than the Sun. A low temperature coupled with high luminosity tells us that the star must be huge, luminosity and temperature giving a radius of about 3 Astronomical Units. It is so big that astronomers can easily detect and measure the size of its apparent disk, which gives an even bigger radius of 3.8 AU, three-fourths the size of the orbit of Jupiter." (from a Univ of Illinois site on stars -- http://www.astro.uiuc.edu/~kaler/sow/sowlist.html ? http://www.astro.uiuc.edu/~kaler/sow/antares.html)The brightest and most massive known stars in our galaxy are Eta Carinae and Pistol. They have estimated masses of 100-150 solar mass (vs 15.5 solar mass for Antares) and are characterized as hypergiant stars. (A new hypergiant star found in infrared in 2002 may have have mass 150-200 suns). But curiously the radiuses of all these hypergiants are estimated to be substantially smaller than Antares: Piston at 320 solar radius and Eta Carinae at 130 solar radius.
Here is a great photo showing glowing gas and dust out to 100 light years around the hypergiant star Eta Carinea.

Glowing gas and dust around one of the brightest and
most massive stars in our galaxy (Eta Carinea) taken in infrared by Spittzer
telescope (image spans 200 light years, in false color)
Cepheid
luminosity-period relationship --- uncalibrated standard candle (12/14)
(The genesis
of writing about cepheid variable stars well defined luminosity vs period
relationship was a play sent to me that I read about Henrietta Swan Leavitt's
work and life, 'Silent Sky' by Lauren Gunderson.)
In the early 20th century at Harvard observatory (astronomer) Henrietta Swan Leavitt made a breakthrough that led to a better understanding of the size of the universe. Hubble later used her data to show that Andromeda was too distance to be in the Milky Way, proving that other galaxies besides the Milky Way existed. Henrietta Leavitt was employed as a 'computer', women who analyzed and characterized the stars on large glass plate photographs of the sky. She specialized in cepheid variable stars, and she found lots of them in photographs of the small magellanic cloud taken by a 24" Harvard telescope in Peru. Individual cepheid variable stars can be seen at a considerable distance, even in nearby galaxies, because they are very luminous, massive young hot stars.
Pressure feedback loopAfter years of studying the resulting large mass of cepheid data she found a striking pattern. The light curve of cepheid variable stars shows a repetitive brightening and dimming that is very regular, probably due to the star physically swelling and shrinking in size, the balance between gravity and outward radiation pressure being unstable. The period of cepheids varies hugely, more than a factor of 100. Leavitt found the period varied from a day to over 100 days. At first it was noticed qualitatively that the long period cepheids were brighter and short period cepheids were dimmer. By 1912 when the detail light curve of 25 cepheids in the small magellanic cloud had been obtained, it was found that all the data fell on a straight line. Cepheids had a linear relationship between period and magnitude! This was a real breakthrough.
In all stars with continuing nuclear reactions the size of the star is set by a pressure balance, gravity pulling in and heat and photons from the core pushing out. There's a high gain negative feedback mechanism operating here, since the rate of the nuclear reactions in the core is very strongly dependent on pressure and density in the core, which in turn depends on the size of the star. In most stars like the sun this feedback loop is stable, a star has fixed size set by its mass and hydrogen/helium ratio. However a few stars within a narrow ranges of mass, age and atomic makeup have pressure loops that are not stable, they oscillate. The most famous class of oscillating stars are the cepheid variables. Of cosmological interest are large, luminous cepheid stars whose light output varies measurably and regularly as the star's size and surface temperature pulse up and down.
This relationship fell out because all the cepheids being analyzed were in the small magellanic cloud, now known to be a small satellite galaxy of the Milky Way very distant from earth. I am not sure exactly what the understanding of the small magellanic cloud was in the early 20th century, but telescopes of the time showed it to be a huge, tight collection of stars isolated from the rest of the Milky Way, so from this is was probably clear that it was likely near edge of the galaxy and quite distant from earth. The latter was the key. If all the small magellanic cloud cepheids were distant and packed into the same tight cloud, then it could be assumed they were approximately the same distance from earth. Hence difference in brightness (in the photographs) must be due to a difference in their intrinsic luminosity, so a plot of period vs brightness can be considered a plot of period vs luminosity, which is much more useful.
Astronomers are good at measuring variations in astronomical objects with time. Position and orbits have long been measured and with the advent of photographs and repeated observations variations in brightness could also be measured. With a known, linear relationship between period and magnitude cepheids in various parts of the sky with the same period could be assumed to have the same luminosity, i.e. the same intrinsic brightness. Thus Leavitt's linear period vs luminosity relationship immediately allowed measured magnitude differences to be translated into distance ratios. In technical jargon Leavitt's relationship was an uncalibrated standard candle.
In the early 1920's Hubble found some cepheids in Andromeda, which were about x100 times dimmer than the cepheids Leavitt found in the small magellanic cloud (for same period). This meant they must be about x10 further away from earth than the small magellanic cloud cepheids, and since the small magellanic cloud was assumed to be near the edge of the galaxy, it meant that Andromeda was too far away to be in the Milky Way, it had to be a separate galaxy! This answered one of the great questions of the age, whether the universe was just the Milky Way, favored by many astronomers, or whether some of the nebula in the sky were separate island universes.
Here is the data from the 1912 Harvard report under director Edward Pickering's byline. He begins by saying this report was prepared by Miss Leavitt. The linear relationship (right) of both the maximum and minimum brightness vs (log) period for all 25 cepheids is quite striking. The brighter, and presumably the bigger, the cepheid the slower it oscillates.
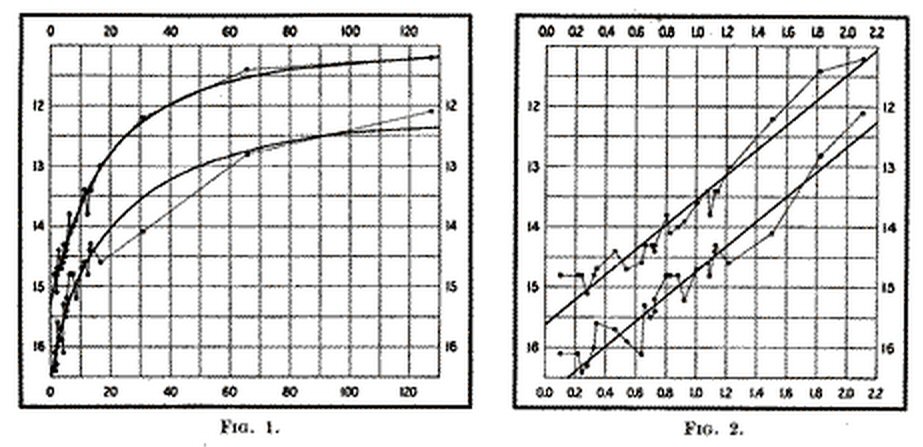
1912 Harvard report on luminsity vs period for 25
small magellanic cloud cepheid variable stars
(left) magnitude vs period (in days)
(right) magnitude vs logarithm of period
( "logarithm of the period increases by about 0.48 for each increase of
one magnitude in brightness")
http://cwp.library.ucla.edu/articles/leavitt/leavitt.note.html
Absolute
cepheid distance --- calibrated standard candle
Leavitt's
relationship was the first step toward finding absolute distances to cepheids.
It is similar to how the absolute dimension of the solar system were discovered.
It was a two step process. Kepler in his analysis of the orbits of the
planets way back in 1619 found a mathematical relationship between a planet's
orbital period and its distance from the sun [(period^2/radius^3) =
constant (dependent on mass of sun and gravitational constant)]. Since
orbital periods for all the planets were known, Kepler's third law allowed
the calculation of the ratio of all the planets' orbital radii.
It was only needed to find one absolute distance, says earth to sun or
any of the planets, and the absolute distance to all the planets from the
sun would be known.
The ancients using eclipse data and the half angle of the moon came up with rough estimates of the earth to sun distance in terms of earth radii. In the 1700s major expeditions to monitor the transit of venus (across the sun) from different locations on earth produced a considerably more accurate determination of the earth to sun distance, again in terms of the earth radii, which by this time had been accurately determined.
Leavitt's period vs magnitude relationship is analogous to Kepler's law in that it allows measured brightness differences (for same period) to be converted into distance ratios. To calibrate Leavitt's relationship it was necessary to find the true distance to a few nearby cepheids by triangulation (parallax), where 1 arc-sec is 3.26 light year. The Dane Hertzsprung attempted to do this around 1920, but his results were wildly off (wrong by about a factor of 10). One of the design goals of the Hubble telescope was specifically to accurately measure the true parallax distance to nearby cepheids, and for this purpose it could use one of its pointing gyros, which can measure angle to 0.001 arc-sec accuracy. It obtained parallax distances for 10 nearby cepheids accurate to about 10%. In the many years since Hubble was designed a couple of specialized satellites have been deployed to very accurately measure parallax of thousands of stars out to a considerable distance. Many years after Leavitt and Hubble in 1940s the absolute distance to Andromeda was adjusted upward about x4 when it was found there exists two classes of cepheid variable stars with slightly different period vs luminosity relationships.
http://hubblesite.org/hubble_discoveries/science_year_in_review/pdf/2006/cepheid_calibration.pdf
--- NASA article on cepheid calibration
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
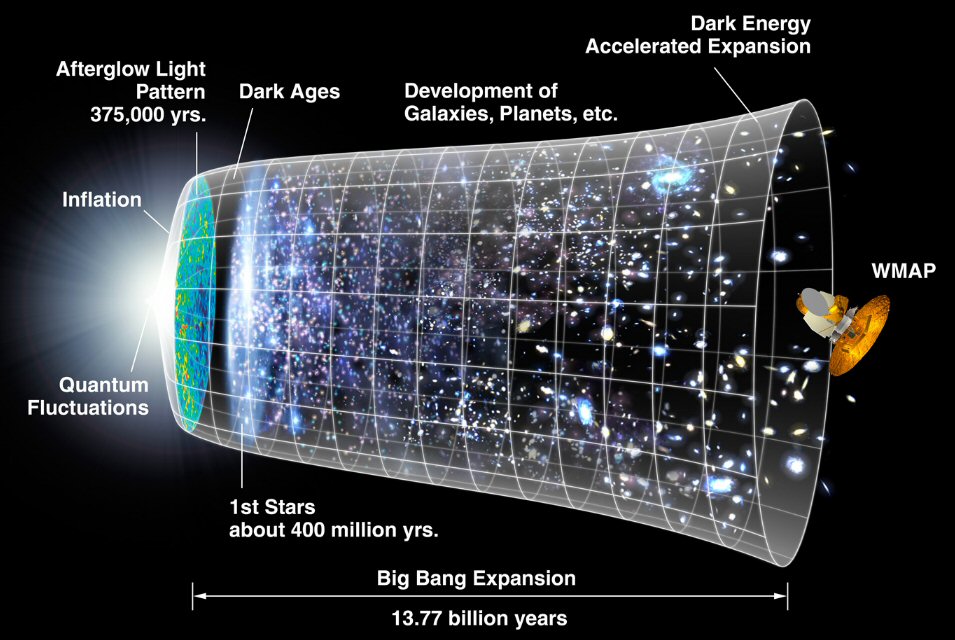
The cosmic radiation sphere we see around earth is the farthest thing out we can see. It was 'created' as a visible entity when the universe turned from opaque to transparent as the universe ceased being a plasma as electrons dropped into orbits around protons. As stated below, this is dated at 375,000 years after the big bang.
The photons were constantly interacting with the plasma through Thomson scattering. As the universe expanded, adiabatic cooling caused the plasma to cool until it became favourable for electrons to combine with protons and form hydrogen atoms. This recombination event happened at around 3,000 K or when the universe was approximately 379,000 years old. At this point, the photons scattered off the now electrically-neutral atoms and began to travel freely through space, resulting in the decoupling of matter and radiation. (Wikipedia -- Cosmic microwave background radiation)Age of universe 13.77 billion +/- 1/2%
The NASA Wmap site has this neat figure showing the timeline of the universe from the time of the big bang to the present. Vertical is the universe's size (radius, either not to scale or logarithmically) vs time horizontally. The Wmap data also allowed the various components of the energy of the universe to be determined, which (in round numbers) was found to be: 5% matter (baryons), 25% dark matter, and 70% dark energy (cosmological constant).
The age of the solar system has been determined extremely accurately (to within one million years) by dating meteorites. I heard this from a meteorite expert on a TV science show, and Wikipedia agrees giving about the same number to four decimal places. This age is determined from radioactive element ratios in the meteorite minerals. Wikipedia says the sun is probably about 30 million years (0.03 billion) older than earth, which scaling from the best earth estimate, gives about the same age as the solar system.
Age of solar system 4.567 billion +/- 0.02%
The age of the earth can only be bounded. The upper limit being the age of solar system meteorites minus the time various models give for the earth to acrete (few million to 100 million says Wikipedia), and the lower limit radioactive dating of the oldest rocks found on earth (small crystals of zircon from the Jack Hills of Western Australia).
Age of earth
4.54 (best estimate)
4.404 to 4.56 billion (limits)
Lifetime of
low mass stars
Stellar fusion
reaction rates depend very strongly on core temperature, and higher mass
stars have higher core temperatures. The result is that high mass stars
burn through their supply of hydrogen far faster than low mass stars. A
rough rule of thumb is stellar main-sequence lifetimes vary with mass by
1,000:1, or 100 million years to 100 billion years. But I came across a
1996 paper (below) that calculates the lifetime for the lowest mass stars:
0.08 to 0.25 solar mass (M type red dwarfs).
0.08 solar mass
10^13 years (10,000 billion years)!
0.25 solar mass
10^12 years (1,000 billion years)
The universe is about 14 billion years old, so the lowest mass stars which are in existence now have barely used up 0.1% of their hydrogen burning lifetime!
http://iopscience.iop.org/0004-637X/482/1/420/fulltext/
Globular cluster
age
You often see the
statement in astronomy books that globular cluster (compact group of stars
that all formed about the same time) are known to be old. One piece of
evidence that all the stars in clusters are old is to be found in their
H-R diagrams. H-R diagrams of globular clusters show no blue and white
stars on the main sequence. Since stars generally form with a range of
masses, a cut off of H-R diagram main sequence most likely means that the
cluster stars have been around long enough for their high mass stars to
burn up (most of) their hydrogen and move off the main sequence.
Here is the HR diagram of the popular globular cluster M3 (Messier 3). The center kink at B-V of 0.5 shows its main sequence 'turn-off' as stars begin to stream right (instead of left). The turn-off point is pretty close to the sun's location on the main sequence. The sun's time on the main sequence is estimated to be about 9-10 billion years. The estimated age of the M3 cluster (according to Wikipedia) is 11.4 billion years.
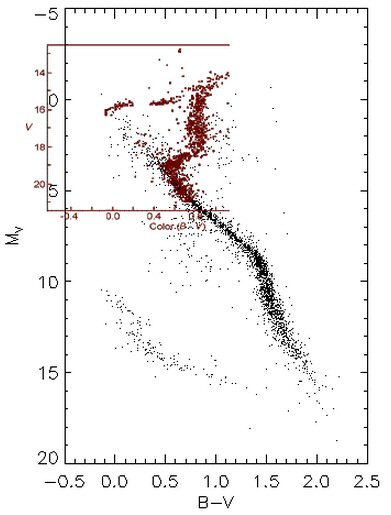
M3 globular cluster HR diagram clearly showing main
sequence turn-off
Here is a Java applet that shows how stars move off the main sequence on the H-R diagram as they transform into giants and then white dwarfs. (This applet could be improved by sketching in the main sequence, so the location of the moving star could be tracked more easily.)
http://www.astro.uni-bonn.de/~javahrd/v071/index.html
Young
earth evangelical perspective
I read a new
book by Karl Giberson, a phyicist who teaches at Eastern Nazarene College,
Saving
Darwin: How to Be a Christian and Believe in Evolution. Giberson points
to a 513 page book by Morris and Whitcomb published in 1961, Genesis
Flood, which presents technical arguments for a 10,000 year old earth
? universe, as being largely responsible for convincing a large swath of
the fundamentalist community in the USA that geologists and astronomers
are all wrong about the age of the earth and biologists are all wrong about
evolution. Here's my long (combo) Amazon review of the the two books:
Title: Christian scientist tries to straighten out his fundamentalist friends, April 17, 2009
This book (Giberson) is in part a nicely written history of the effort by a relatively tiny group of fundamentalist christians who have argued, quite sucessfully if polls are to be believed, that biologists have evolution all wrong and geologists have the age of the earth all wrong. Anti-evolution and young earth views fit well with a literal reading of the bible, and this has resulted in the last 50 to 100 years in these views being adopted by a wide swath of the fundamentalist clergy and community, most of whom are untrained technically.
Giberson is a self described christian scientist whose writing is accurate, technically persuasive, and sometimes even poetic. Clearly one of his aims in this book is to convince his friends in the fundamentalist world that their anti-evolution and young earth creationists views are just plain wrong. In just two pages (p189-190) he shows why evolution (almost) has to be true, listing eight (of many) independent lines of evidence that support it. He could have strengthen his argument if he had included a little math. For example, if each of eight 'independent' arguments for evolution is only 90% likely to be true and 10% likely to be false, then the likelihood of no evolution, which requires all eight arguments to fail, is one in 100 million! (This is figured as 0.1 multiplied by itself eight times.)
I agreed with about 99% of the points Giberson makes in this book even though I am a non-religious engineer. The 1% that bothered me was his making nice-nice with the pied pipers who have have spread the anti-evolution and young earth message which have lead a wide swath of the fundamentalist community into the wilderness. As he traces the history of the creationist movement, Giberson focuses on one book which he argues had the greatest influence on the fundamentalist community: 'Genesis Flood' by Morris and Whitcom published in 1961. The technical of the two authors is the recently deceased PhD engineer/scientist Henry Morris. Giberson had grown up a fundamentalist and had read Genesis Flood in high school and been convinced by it, so Morris, who Giberson calls "a giant of American fundamentalism", was something of a boyhood hero to the young Giberson.
Here are some of the phrases Giberson uses to describe the 513 page Genesis Flood and its impact:
* impressively technical, masterful, entire presentation was very believable
* enough footnotes, graphs, and pictures to convince any intellectually oriented fundamentalist (that the earth was created about 10,000 years ago and there is no reason to take evolution seriously.)
* bombshell, watershed event, what it accomplished was nothing short of astonishing
* perhaps the most influential text on any topic in the second half of the 20th century (This claim for the book is really something, and it caused me to go to Amazon and buy a used copy of the Genesis Flood.)
Later in the book Giberson refers to popular creationist arguments as "rubbish" and has a whole page listing the tricky and deceptive arguments "used to great effect in virtually every creationist text". But curiously Giberson never singles out Morris, who he has identified as the chief pied piper, for criticism. Maybe this is because he was a friend, or maybe because Giberson thinks there has been too much name calling in the evolution/creationism fight. Issac Asimov said, "Creationists are stupid, lying people" (p138) and Richard Dawkins has called them, "Stupid, Wicked and Insane" which Giberson uses for a chapter title.
I was also a little disappointed that Giberson never addresses the bigger picture of how christian theology is a poor fit to the continuum of life and random nature revealed by evolution. For example, Giberson mentions the meteorite that wiped out the dinosaurs 65 million years ago, but he doesn't even comment on it. Clearly this was a one time random event. It might have missed the earth or have been a little smaller in which case dinosaurs might still be around and almost for sure we'd not be here now. If it had been a little bigger, it might have sterilized the surface of the earth, forcing life on earth to re-evolve from underground or underwater microbes, in which case almost for sure we'd not be here now. Does christian theology make any attempt to deal with random turning points like this in life's history? Not that I've seen. Can a theologian please tell me: if the meteorite had been a little smaller, would Jesus still have arrived around zero BCE and instead of being squeezed out of Mary, have popped out of a dinosaur egg?
On Morris and Genesis Flood
I dipped into Genesis Flood to see how Morris operated. Typical is Morris' discussion of radioactive dating of the earth. For 20 pages or so Morris quotes and footnotes every published reference he can find that says earlier dates were wrong, and he discusses every known measurement error of the procedure. Arthur Holmes, who Morris mentions (p334), had already determined the age of the earth by 1913 via a primitive radioactive decay procedure to be 1.6 billion years, off by only a factor of three from the currently accepted age. These relatively small errors discussed in the geology literature have 'zero' relevance to the Morris ? Whitcom position that the earth is only 10,000 years old. There is a factor of 'one million' between 4.6 billion and 4.6 thousand! Finally many pages into the technical discussion of radioactive techniques, probably reached only by the persistent reader, Morris owns up to the fact that even if the measurement errors were off by a factor of ten they would still yield an age for the earth of more than 100 million years, far in excess of his 10,000 years. He doesn't do the math, but 100 million is x10,000 longer than his 10,000 years.
So what's Morris' rebuttal to radioactive dating? It's that god created the radioactive parent/daughter ratios in the rocks so the earth would "appear" old! And why is it that all the various geochronometer methods involving different elements and isotopes yield ages close together? I quote his response, "In the absence of a specific revelation, it seems impossible to decide this question with finality." (p346) Translation --- I couldn't figure out an explanation for this one.
Morris, who minored in geology (says Giberson), knew exactly what he was doing in this book. He was not 'uninformed' as Giberson says at one point. All the hundreds of footnoted pages discussing various age measurement errors are smoke screens, inserted for misdirection, for confusion, to lend supposed scientific credibility to Morris' and Whitcom's biblically inspired answers. The pattern repeats again and again.
Astronomical dating --- Stars 'appear' to be billions of light years away, because god created photons 'in flight' says Morris. The HR diagram (Hertzsprung-Russell or luminosity vs color diagram) has been around since 1914. It is a powerful tool for estimating the age of stars in clusters. From basic stellar physics and observation it is known that large, bright stars burn through their supply of hydrogen much, much faster (x1,000) than small dim stars, so large stars can have lifetimes of 20 million years vs 20 billion years for small stars. By plotting stars in a cluster on an HR diagram and seeing where the brighter, faster burning stars go missing (technically move off the main sequence), a rough estimate of the age of the cluster is obtained. When this is done for some large star clusters in the halo of our galaxy, an estimated age of 13 billion years is obtained, about three times the age of the earth.
So how does Morris deal with this? He doesn't deal with it, there's no mention of HR diagrams or star clusters. He just waves his arms saying cosmology is speculative (HR diagrams have nothing to do with cosmology) and astronomical dating is less firmly grounded than radioactive dating (granted), so it's not worth considering. Now there's a non-sequitor.----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
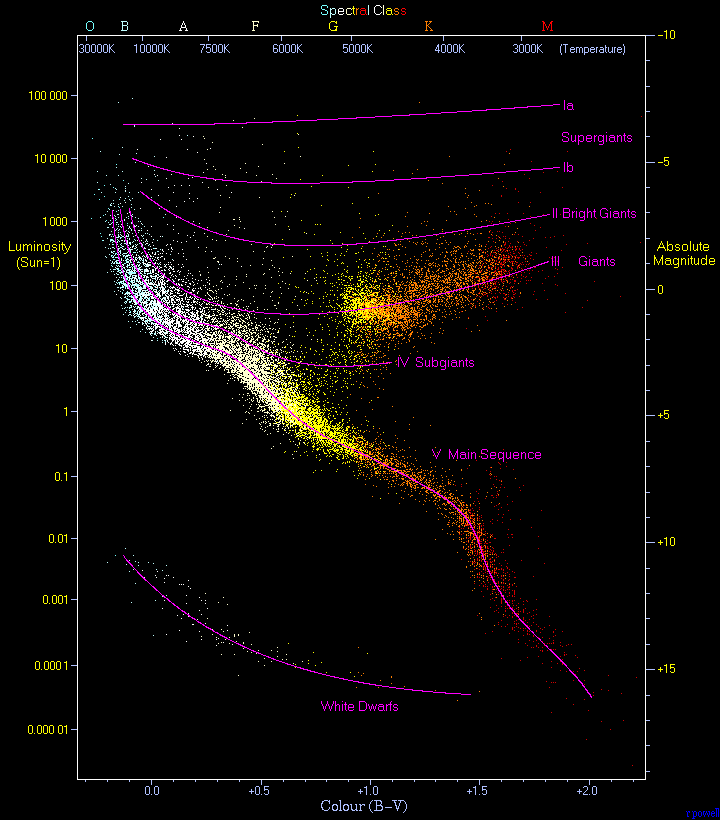
Most stars in an H-R diagram fall along a narrow sweeping diagonal that runs from the upper left corner (blue and very bright) to the lower right corner (red and very dim) called the main sequence. When H-R diagrams were first drawn, little about star physics were understood, so these diagrams provided clues and tests for stellar theories. The classic color spectral classification of stars was devised at Harvard in 1890 and is still used. It is remembered with the pneumonic: 'Oh, Be A Fine Girl, Kiss Me', which apparently was ginned up by the same person at Harvard who developed the classification system. The sun is a yellow G star.
O blue
B
blue
A white
F yellow-white
G yellow
(sun)
K orange
M red
We now know that all the stars on the main sequence are burning hydrogen to helium (like the sun) and that the location of a star on the diagram depends (almost entirely) on its mass. High mass stars burning hot and fast look blue and bright, while low mass stars burning cool and slow look red and dim. Stars in later stages of their life (giants and dwarfs) form other recognizable patterns on the H-R diagram.
Here is a terrific HR diagram (from Wikipedia) with real data, thousands stars from star catalogues are plotted showing their color too. Notice the main sequence, dwarfs, and giants do cluster nicely, but bigger, brighter stars scatter all over the top of the diagram.
Notice in the diagram how dim the dwarfs and low mass, class M main sequence stars are. When a main sequence star, after going through the giant phase, ends up as a dwarf its luminosity is reduced hugely (factor of 1,000 or more). The closest stars to the earth is the triple system Alpha Centauri (4.35 ly). Two of the Alpha Centauri triplet are sun-like stars that are the 3rd and 4th brightest stars in the sky. (The 1st and 2nd brightest stars in the sky are Sirius A at 8 ly and Procyon A at 11 ly.) Alpha Centauri's 3rd star, a low mass M5 red main sequence star, is far too dim to be seen with the naked eye. In dark conditions the eye can see down to 6th magnitude, but the Alpha Centauri red M5 star appears in our sky as an 11th magnitude star even though it is the closest star to earth!
Proxima Centauri (in the corner)
The dim M5 star in the Alpha Centauri triple system is named Proxima Centauri. This tiny red dwarf is a main sequence star is tucked tight into lower right corner of the H-R diagram [B-V color index of 1.90 and absolute magnitude of 15.5]. Because it is so close (4.24 ly) its angular dia can be measured using optical interferometry allowing its mass to be estimated at 0.12 solar mass and its lifetime at 4 trillion years.
Brown dwarfs
Brown dwarfs,
at least those that formed at the center of a gravitational collapse in
a hydrogen cloud, are 'failed stars'. They are a class of stellar like
objects, typically with much more mass than jupiter, but still below 0.075
solar mass (about 75 jupiters) needed for the lowest mass stars. When they
collapse, they don't 'turn on'. The conversion of gravitation energy to
thermal energy of their collapse does not heat them enough to initiate
hydrogen fusion. While they can start off pretty hot, they slowly radiate
their energy away, mostly in the infrared, as they cool down.
Brown dwarfs are too cool to fuse (ordinary) hydrogen to helium, but still in the mass range below x75 jupiter two other types of (limited) fusion are possible. Lithium will fuse at a lower temperature than hydrogen, and deuterium at a still lower temperature. The mass threshold for lithium fusion is x65 jupiter and x13 jupiter for deuterium fusion. Below 0.012 solar mass (about x12 jupiter mass) no fusion is possible. So there are really three types of brown dwarfs: smallest with no fusion, mid-mass range with only deuterium fusion, and lithium fusion when mass is close to, but still below, the mass threshold of (true) low mass stars. In fact a test astronomers use to find (mid-mass) brown dwarfs, to separate them from dim low mass stars, is to look for the presence of lithium in the spectrum. Lithium rarely exists in a star's spectrum since a newly formed star burns its initial supply of lithium quickly (100 million years). A dim stellar class object, if over 100 million years old, that has lithium in the spectrum is a brown dwarf (says Wikipedia).
Brown dwarfs were theorized to exist in the 1960's but (with one exception) no brown dwarfs were observed until an earth based infrared (1.2 to 2.2 micron) survey of the sky was done starting in 1997. In six years 173 brown dwarfs were found many of them quite close (20 light years). Surface temperatures are like 600-700K or about 1/10th the sun's surface temp. Since the radiant energy goes as T^4, their radiated energy (in addition to peaking in the infrared) is very low. Many more brown dwarfs have been found since a new satellite that observes in the infrared went up, now about 2,000 are known. Wikipedia says a few brown dwarfs are known to have planets.
Lithium in stars
One indicator of
a brown dwarf is it contains lithium. A small amount of lithium (element
#3) was made by the big bang. Main sequence stars contain little to no
lithium because lithium mixed with hydrogen 'burns' to helium at a temperature
just a little below the temperature at which hydrogen fusion to helium
begins (2.5 million K). The largest brown dwarfs (above .062 solar
mass or 65 jupiters) do eventually warm up enough in their core that they
begin to 'burn' their lithium.
T
Tauri stars -- young stars without fusion (2/13)
Recently reading
Scientific American I learned about a class stars I never heard of. They
are in many ways like the sun, shining brightly in the yellow red, but
they have NO internal fusion, none. These are T Tauri stars, named after
a start called T Tauri, only a million years old and fairly close to earth
(460 light years) discovered as a variable star in 1852. These are young
'stars' still contracting, and it is the energy released by the gravitational
contraction that they are radiating. A T Tauri star with the mass of the
sun would have surface temperature like the sun (5,500C), but a larger
diameter so it would shine more brightly. Clearly, as our local T Tauri
star shows, at one million years they are already shining, and it takes
a "few million years" (says Wikipedia) before the core gets hot enough
for thermonuclear fusion to begin, which probably sets the lifetime of
the 'no fusion' class of T Tauri stars at a few million years.
Wikipedia describes these young 'no fusion' stars as pre-main sequence stars. They don't fuse hydrogen yet because their cores have not reached the hydrogen ignition temperature. The T Tauri Wikipedia article says it takes T Tauri stars about 100 million years to reach the main sequence (start hydrogen fusion). Some classes of T Tauri stars have lithium in their spectrum like brown dwarfs, but lithium is missing from normal main sequence stars. Protostars (presumably) start with lithium from the big bang and a T Tauri star that has no fusion of course retains it original supply of lithium. As the core temerature is approaching the hydrogen fusion ignition temperture, what happens first is that the star begins to 'burn' its lithium as this reaction goes at a temperature just slightly below the hydrogen fusing temperature. Depending on how much convection there is in the star (depends for example on rotation rate), the star can stay off the main sequence for millions more years powered by the burning of its lithium.
It's interesting that a one solar mass star typically takes something like 0.1 billion years after its protostar phase to make its way onto the (hydrogen fusion) main sequence, going first through a 'no fusion' T Tauri phase of shining brightly due to gravitational energy release, followed by a period of burning most of its (big bang supplied) lithium.
Orion
molecular cloud and Orion's belt stars
One of the
brightest and most easily recognized object is the sky is Orion's belt,
which is three bright equally spaced stars in a row. These three
stars are all blue-white super giants with about 20 times the mass of the
sun and about 10 million years old. Super giant stars have to be young
because their high internal pressure causes them to run very hot and to
burn through their fuel quickly. These stars are all relatively close at
1,500 light years (1.5% the diameter of the galaxy) and were formed at
the same time from the huge Orion molecular cloud in which they are embedded.
This is the closest region to us where a lot of new stars are forming.
The Orion hydrogen gas cloud is huge in our sky spanning 13 degrees!
There are spectacular pictures of it online.
http://antwrp.gsfc.nasa.gov/apod/ap070125.html
http://antwrp.gsfc.nasa.gov/apod/image/0701/oriondeepwide_gendler_f.jpg
Star
formation and dynamics of molecular clouds
As
far as is known, newborn stars form only in molecular clouds, which are
mostly molecular hydrogen. Large clouds have enough mass to form as many
as 1 million stars the size of the sun. Clouds when undisturbed are more
or less stable due to magnetic fields and turbulent motion that stir them
up, so it difficult for the force of gravity to cause it to collapse.
For gravity to cause a region of the gas to condense into a star the gas
must be very cold (only about 10 degrees above absolute zero). Carbon
in the cloud contributes to the ability of the cloud to cool by radiating
heat, hence carbon promotes star formation.
The first link below is a spectacular picture of shock wave from one massive blue giant Wolf-Rayet star (10-20 solar mass) hitting a molecular cloud. 2nd link is another spectacular picture of a shock wave; this one from a burst of massive young stars in a cluster on the edge of the small Magellanic cloud (satellite galaxy of the Milky Way).
http://antwrp.gsfc.nasa.gov/apod/ap070130.html
http://antwrp.gsfc.nasa.gov/apod/ap070110.html
Generally star formation in a cloud is catalyzed by an outside event, often a supernova explosion of a large star outside the cloud. A supernova blows most of its mass into space which expands forming a shock wave. When a supernova shock wave hits a cloud, it compresses some of the mass of the cloud allowing gravity to take over and continue the contraction.
There is a negative feedback effect that strongly limits star formation in a cloud. When some hot stars do form within the cloud, their radiant energy heats the gas effectively blocking, or substantially slowing down, further star formation. Only about 1% of the mass of the cloud will be converted to stars before the heating of the cloud stops star formation. This is the main reason why 13.7 billion years after the universe and galaxies came into existence molecular clouds are still around and new stars are still forming.
The combined effect of large stars heating and dispersing their parent cloud, followed the stars going supernova about 10 million years later and their shock waves catalyzing star formation in nearby clouds, results in waves of star formation that slowly sweep through the galaxy. In other words the process of star formation is self-propagating.
Mass of stars
Contrary to
what you may have read, the sun is not an average star. Our sun is bigger
than 95% of stars in our galaxy (Milky Way). The mass of stars ranges from
roughly 1/10th the mass of our sun to about 50 times the mass of the sun.
For a normal hydrogen burning (main sequence) star the brightness (luminosity)
goes up very strongly as the mass goes up. Luminosity varies as mass to
the 3.5 power (luminosity = mass^3.5). A two solar mass star is more than
ten times brighter than the sun, and a ten solar mass star is more than
3,000 times brighter. The reason brightness varies with mass is that the
fusion rate in the core depends strongly on the pressure in the core, which
depends on the mass of the star.
Solar models tell us the lifetime of the sun (as a main sequence star) will be about 10 billion years. The earth and the sun formed about 4.6 billion years ago. Stars with high mass have very short life times because they burn their fuel so fast. A large blue star with 30 solar masses will have a very short lifetime of 2 million years.
What controls solar lifetime?{30 solar mass/(30^3.5 brighter)} x
The reaction time of proton-proton fusing (vs temperature) is primarily what controls how fast a star burns hydrogen, i.e. how long it remains on the main sequence. At 15 million degrees kelvin in the core of the sun the proton-proton reaction rate is very slow,. A proton typically lives 8 billion years (!) before fusing with another proton (to form deuterium). Compare this to deuterium (proton + neutron), which only lives about one second before fusing with a proton to form He 3. (The proton-proton fusion rate is very temperature sensitive varying as (approx) T^4.)
Compare that to a very small red star with 1/10 solar mass. It has a lifetime several hundred times the present age of the universe.
{0.1/(0.1^3.5} x. 10 billion years
= 300 x 10 billion years
= 3,000 billion years
Bottom line --- star mass varies only modestly, but star lifetime and brightness vary enonomously. The intensity formula shows that star intensity varies over almost a billion to one range {(30/0.1)^3.5 = 470 million)! Star lifetime varies over roughly a million to one range (3,000 billion yr/2 million yr = 1.5 million).
Aside --- mass of stars in binary star systems can be determined by measuring the distance between them and the period of rotation.
Interesting fact --- No star with less than 0.9 solar mass has ever died a (natural) death, because these stars all have lifetimes longer than the age of the universe (about 13-14 billion years).
Stellar metallicity
Metallicity
is one of the major ways of classifying stars. It is a measure of the chemistry
of the star, a measure of what fraction of the star is made up of elements
other than hydrogen and helium. A star might be classified as having, say
1% or 10% of the metallicity of the sun. In a main sequence star the only
element the star creates is helium, so any elements above helium must have
been present in the material out of which star formed. All these 'metals'
(as the astronomers call them) found within stars has come from the residue
of earlier generations of stars that seeded the gas clouds out of which
stars form. Elements up to element 26 (iron) are created by large stars
of different sizes. Elements 27 and higher are created during the supernova
explosions that ends the fusion lifetime of stars larger than about 8 solar
masses, and the supernova blows these metals into space.
The amount of metals in a star can be estimated by looking at the strength of various metal lines in the spectrum of the star. Stars with low metallicity were probably born early in the lifetime of the galaxy, before its gas clouds were strongly enriched by generations of fast burning stars, so the level of metallicity provides a clue to the age of the star. It's also been found that how stars move (direction and speed relative to the sun) is correlated with the star's metallicity. For example, halo stars that spherically surround the galaxy have very elliptical orbits and are also low in metals indicating that they are old stars.
Nearby
halo star -- Kapteyn's Star
About 1 in 1,000
of stars in the disk are thought to be (from their metallicity and speed)
halo stars that just happen to be passing through the disk. One suspected
halo star is very near to the sun, it is Kapteyn's Star, a dim red subdwarf
just 12 ly away. Its speed (relative to the sun) is 245 km/sec, which is
about x10 higher than most nearby stars, and it has metallicity of 32%
of the sun. Subdwarf stars burn hydrogen, but on an H-R diagram lie slightly
below the main sequence. This is because their low metallicity affects
their opacity causing them to run a little hotter, smaller, and dimmer
than main sequence stars of the same mass.
Distance
to Milky Way stars
The
distance to many stars out to about 300,000 light years, which includes
all the stars in out galaxy, can be estimated from the Hertzsprung-Russell
diagram. Just measure the color (using spectrosopy) of the star,
and using its type (main sequence, white dwarf, etc) go into the H-R diagram
and read off from the vertical axis the true (intrinsic) brightness (relative
to the sun). Combine its true brightness with its measured (apparent) brightness
and square law rule and you have an estimate to the distance of the star.
Here is a link to a nice lecture describing how the astronomical distance scale has been constructed:
http://terrytao.wordpress.com/2009/09/06/two-more-clay-mahler-lectures/
Star winds and
mass loss
Giant stars
have low gravity out near their edges with the result that powerful winds
blow from their surfaces into space resulting in a substantial loss of
mass. Some of the gas condenses into molecules and dust. There may be so
much dust emitted that the star is buried in it, showing up only only as
an infrared glow of heated dust. Oxygen-rich giant stars make silicate
dust, while carbon stars make carbon-dust similar to graphite and soot.
Most of the dust that inhabits interstellar space is made this way. A star
during its giant phase can blow off (as wind) as much as half of its mass.
Earth
like planets around red dwarf stars
800 extra-solar
planets have now been found. The first planets were found by studying wobbles
(over time) in the position of nearby stars, but with new satellites, like
NASA’s Kepler mission, lots of new planets are being found using the solar
transient method. Kepler looks for transient dimming in 150,000 stars.
This method for finding potentially habitable, earth size planets works
particularly well with red dwarf stars.
First, there are a lot of red dwarfs, an estimated 75 billion in our galaxy (of 100 to 200 billion total) are red dwarfs. Wikipedia gives the red dwarf mass range as 0.075 to 0.5 solar mass. Second, the smaller the radius of a star the easier it is to detect smaller planets because they block out a larger fraction of the light. To put some numbers on this, the earth is roughly x100 smaller in dia than the sun, so to an outside observer (if there are any!), a transient of the earth reduces the sun's brightness by 0.01% (one part in ten thousand). Third, planets orbit closer in around a low mass star, and the habitable zone is further in, so more transients can be observed in a given time.
OK, red dwarfs are dim red low mass stars, but how much smaller are they? Actually I had no idea. If a red dwarf had 1/10th mass of the sun how big would it be? Simple mass scaling would reduce the dia by 2.25 = (10^.333), but since it's cooler with lower thermal pressure, doesn't that reduce its size more? (apparently it does)A few dozen candidate earth size planets orbiting red dwarfs have now been detected using the transient method. This is enough to do some statistics. If planet orbit planes are randomly oriented with respect to the earth, which I assume is the assumption, then we will see only a small fraction of planets transiting a star. Crunching the numbers a recent estimate is 6% of red dwarf stars have earth-sized planets at the right distance from the star to be potentially habitable. Since a large fraction of stars in the Milky are red dwarf stars, that means on average the spacing between earth-like planets is only 13 light-years (amazingly close).A table in Wikipedia ('red dwarf') shows that solar models predict the radius tracks the mass, so a large red dwarf with half solar mass has half solar radius, and at the bottom end (just above brown dwarfs) an 8% solar mass red dwarf has 8% solar radius. The smallest red dwarf dia ever 'measured' is about 1/8th of the sun. This would increase the dimming of an earth size planet transient by x 64 to 0.64%.
To put that in perspective only about three dozen stars are within 13 light years of earth. Wikipedia says 20 of the closest 30 stars to earth are red dwarfs, including the closest (4 light years) Proxima Centauri. Even though they are close not a single red dwarf star is visible to the naked eye.
Supernova
A key fact
about supernovas (new to me)
"Until this year, no astronomer had ever seen a supernova explode. That is because it only begins to emit visible light — the thing astronomers have historically been good at detecting — some time after (like a month!) the explosion has begun. To catch a supernova at the moment of detonation, you have to be looking in exactly the right part of the sky and looking for X-rays, which burst outward and then fade rapidly in the first instants of a supernovas life." (6/1/08 NYT Editorial)A May 2008 NYT front page story reported that in early 2008 when the Swift gamma burst satellite was looking at a galaxy (NGC2770) to follow up on a supernova a few weeks old, by incredible luck it detected a brief (few minutes) burst of x-rays indicating another supernova in the same galaxy had just occurred. (Two supernova so close together in time is statistically unlikely since even a large galaxy like our Milky Way has a supernova only about once a century. There hasn't been a supernova in our galaxy since the 1600's.)
"(Swift) recorded an unexpected burst of invisible X-rays 100 billion times as bright as the Sun. Most supernovas, Dr. Soderberg explained, are discovered and classified by their visible light, but that typically does not happen until the explosion is a month or more old and has brightened enough to be seen over intergalactic distances. The true fireworks, she said, happen much earlier when a shock wave from the imploding core hits the star's surface, producing so-called breakout light, which lasts only a few minutes." (NYT May 22, 2008)The interesting fact is the claimed month delay between the actual collapse (which I have always understood to be minutes to hours, certainly much less than a day) and detectable light emission. Maybe they mean the peak of the optical brightness, but I thought that happened quite quickly too, in a day or two. This is a Type Ibc supernova, the collapse of a high mass star, thought here to be a Wolf-Rayet star. Need to read up on this. Either their must be some obscuring layer that needs to clear, or maybe the radiating surface needs to expand.
Gamma ray bursts
One gamma
ray burst, estimated to have been 10 billion light years away or basically
on the other side of the observable universe, was so bright that if you
happened to have been looking at the right patch of the sky with just with
binocularsyou
could have seen the after glow! (ref: reputable astronomer on Discover
'Universe' TV show 2010). They are the brightest thing in the sky,
or as Wikipedia puts it --- "They are the most luminous electromagnetic
events known to occur in the universe. Bursts can last from milliseconds
to several minutes, although a typical burst lasts a few seconds." Distances
are figured from red shifts of optical (and x-ray) after-glows that are
sometimes found were first associated with gamma bursts in 1997.
For a long time (> 30 years) gamma ray bursts were a mystery. The energy in the gamma rays is so high it implies temperatures of billions of degrees. Wikipedia 'Gamma burst' intro gives the source(s) as beams from large mass rapidly rotating stars as they collapses to form black holes, but elsewhere in the article the text is more vague: "(Data) unambiguously links long GRBs (gamma ray bursts) with the deaths of massive stars. What they know is that occasionally gamma bursts and supernovas have been discovered immediately following each other. On Discover 'Universe' TV show, which featured several astronomers from famous colleges (Caltech, Univ of Ca, etc), the source was described as stars stars being ripped apart as they are fall into (apparently) preexisting black holes. These are not the same. Did I hear wrong?
Light curves (after-glows) of gamma ray bursters are amazingly diverse. They are basically all different, and no one knows why. Here are 12 examples from Wikipedia ('Gamma-ray burst'). Very likely the horizontal units is seconds and the vertical is counts from the instrument.
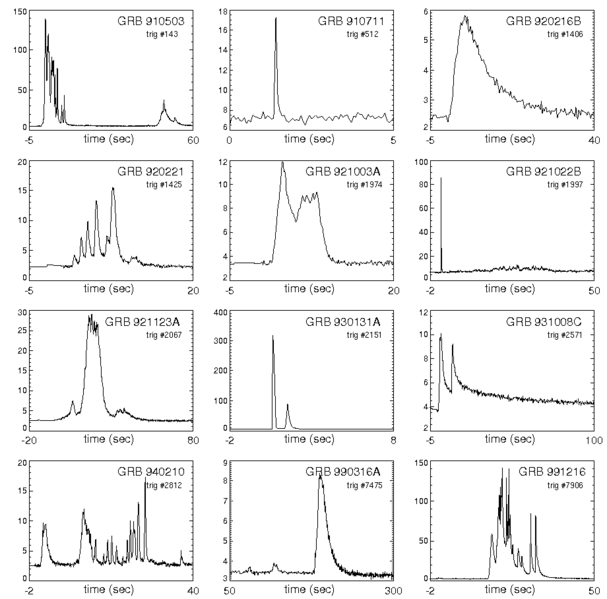
source ---Compton Gamma Ray Observatory 'Burst and
Transient Source Explorer' instrument
in Wikipedia 'Gamma-ray burst'
Extraolar
planetary ring system (Dec 2015)
A complex
light curve (variation in brightness) for a nearby young star (J1407) that
was seen only in 2007 has been interpreted as being due to a transient
of the star by a huge ring system around a large planet of the star. If
the analysis is correct, this is the first extrasolar planetary ring system
ever found. The key to the analysis is a computer model was found that
can duplicate the light curve. There's a feature article about this discovery
in Scientific American (Jan 2016) by one of the researchers, and there
is also a brief Wikipedia
page. The J1407 star, about the size of our sun, is relatively nearby
at 420 light years and is quite young at 16 million years. Its planet
(J1407b) is a super jupiter in size, and the size of this planet's ring
system is huge at 0.6 AU radius (x200 size of saturn's ring system). A
gap in the rings can be explained by a mars size moon of the planet. Because
the star so young the ring system is probably still evolving.
Cool video
showing how a J1407 computer model transient matches the observed light
curve:
https://vimeo.com/117757625
------------------------------------------------------------------------------------------------------------------------------------------------------

Milky Way as barred spiral with Sun (artist conception)
Milky Way dia about 100,000 light year
(box around sun is 400 light year, pie is 6,000 light
year)
(scan from National Geographic, Dec 2009)
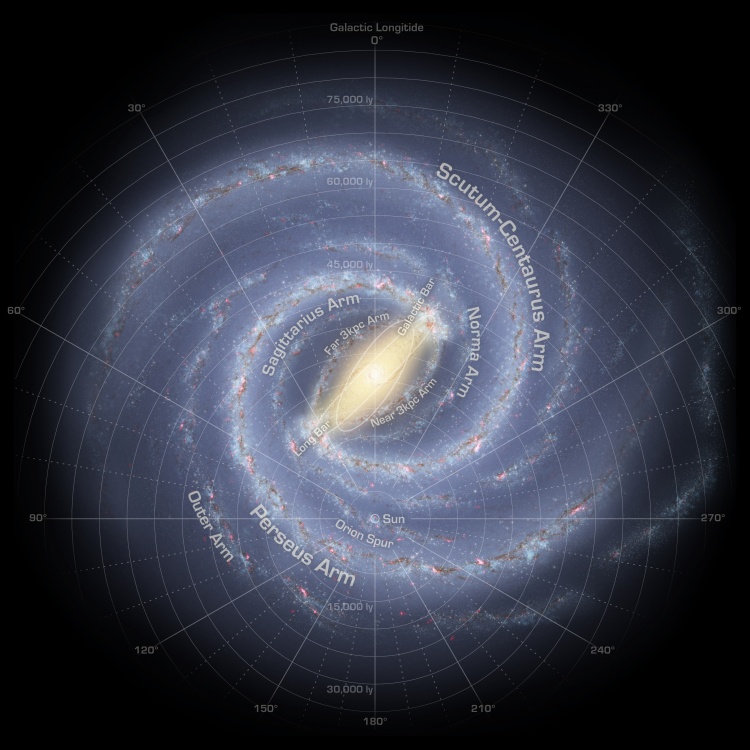
Milky Way as a barred spiral with Sun in Orion Spur
arm (based on Spitzer Space telescope data)
Center of Milky Way
This is a
real photo clearly showing the location of the center of the Milky Way
in the sky. (Never before have I known where the center was.) Snapped with
180 degree wide angle lens at Very Large Telescope (VLT) in Chile.
Telescope is observing center of Milky Way using adaptive optics. They use a sodium laser to make an artificial star that forms at an altitude of 90 km (54 miles) in the mesosphere. Color of the laser is tuned to energise a layer of sodium atoms found there. This layer of sodium atoms is thought to be a leftover from meteorites entering the Earth’s atmosphere. When excited by the light from the laser, the atoms start glowing, forming a small bright spot that can be used as an artificial reference star for the adaptive optics.

Laser to make artificial star for adaptive optics
at Very Large Telescope, Chile
Photo credit: Yuri Beletsky (Aug 2010), Wikipedia
Introduction
to our galaxy
Most stars
in the Milky Way (and other spiral galaxies) are either in the center (bulge)
or have collapsed into a thin disk rotating disk. The thickness of the
disk is only 1%-3% or so of the diameter of the disk. There is, however,
a population of stars, called halo stars, that form (roughly) a sphere
around the galaxy and which tend to have highly elliptical comment like
orbits
The sun is in the disk and since most of the stars we can see well are relatively nearby, these are nearly all disk stars too. But not all of them. About 1 in a 1,000 is a halo star that happens to be diving through the disk in our neighborhood.
A good discussion of our galaxy, with emphasis on the types of stars in it and how it was all figured out, is to be found in this book: Alchemy of the Heavens, by Ken Croswell, 1995.
How stars
in a galaxy rotate
When you see
a picture of stars grouped together into a object with a well defined shape,
like a galaxy or globular cluster (a dense, spherical concentration of
stars), it sort of looks like the stars are just sitting there holding
position. But, of course, that can't be true. Any star not moving (rotating)
will be pulled toward the center by the gravity of the group. Each star
orbits on its own and lots of different orbits are possible. The orbits
can be relatively circular or highly elliptical like comets in the solar
system, or in globular cluster with very high density quite complex and
maybe chaotic.
The swept back arms of a spiral galaxy look so symmetrical that it's tempting to assume a spiral galaxy rotates (sort of) like a pinwheel. Wrong! Stars nearer the center go around faster than stars further out. And the spiral arms, which are marked by a trail of new, bright, blue stars formed from the gas clouds in the arms, rotate at an altogether different rate, a little slower than the stars. While it's true that most stars at a given distance from the center in the disk of the galaxy rotate around roughly together, stars in the halo, and some stars in the disks too, have eccentric, elliptic orbits that go in toward the center of the galaxy loop around and come back out. A few stars in the disk even rotate in the 'wrong' direction, meaning going around the center but in the opposite direction from most of the other disk stars!
Stars in the disk not only go rotate around the center of the galaxy, they tend to oscillate up and down in the disk. They move like horses on a carousel. The reason for this up/down motion is that when the sun gets high in the disk there is a gravitation attraction from the disk downward, and when the sun is low in the disk the force is upwards. As long as there is no damping mechanism, and apparently there isn't, (stars move pretty much independently), once an up/down motion is started it will continue in the same way that rotation around the center continues.
Milky Way's
large black hole
Dramatic evidence
for a (fairly) large black hole (4 million solar mass est) in the center
bulge of the Milky Way is shown in the movie at the link below. The orbits
of stars near the center of the galaxy have been followed since 1995 by
UCLA astronomers using the Keck telescope. 13 years of data have been assembled
into this movie, which shows a lot of star motion including some stars
looping completely around the hole.
Two stars in particular (SO-16 and SO-2) provide strong evidence of a black hole by looping very quickly around the same point in space. SO-2 is shown making nearly a complete orbit around the hole (period of 15.5 yr). SO-16 (upper left) is estimated to come within 90 AU of the hole. (For reference Pluto is at 39 AU, and 90 AU is a (1/2) light-day or 0.03% the distance from the sun to the nearest star.)
http://www.astro.ucla.edu/~ghezgroup/gc/pictures/orbitsMovie.shtml
Andromeda galaxy
Finally a
really great picture of our nearest big spiral galaxy, andromeda (M31).
This picture beautifully shows its structure because this photo is taken
mostly in ultraviolet by a new satellite. It is about 2.5 million ly away
and 140 thousand ly across.

Nasa's GALEX mission
http://www.galex.caltech.edu/media/glx2012-03r_img01.html
Below is a composite image that accurately shows the correct size of Andromeda compared to our moon, and what it would like if Andromeda was brighter and we could see in ultraviolet. Andromeda is about 3 degrees across vs about 0.5 degree for moon. Only the bright core of Andromeda is visible to the naked eye, so without a telescope Andromeda looks much smaller than it does below.

Andromeda and moon composite image with correct sky
sizes
NGC6814 -- classic spiral galaxy
Phil Plait
in his astronomy column on Slate included this Hubble image of a
sprial galaxy NGC6814 because it is so beautiful, a classic spiral. It's
75 million ly from earth (compared to 2.5 million for Andromeda) and a
little smaller in dia than the Milky Way at 90 lg. What's interesting (besides
its classic beauty) is that its black hole at the center is feeding, indicated
from the doppler shifts of the gas near the center, so the center bulge
is brightly lit up. Wikipedia classifies this as a seyfert galaxy with
a highly variable source of x-ray radiation.

NGC6814 hubble image
active seyfert galaxy with classic spiral shape
Interesting aside --- While jupiter is mostly hydrogen and helium, there's some rock-like, earth-like elements in its core. You can think of it as 10-15 earths deep down inside jupiter.As bright as the sun -- an amazing jupiter tidbit
"Within a 1,000 years a jupiter-mass planet can acquire half of its final mass (about 300 earths). In the process it dissipates so much heat that it can briefly outshine the sun."In other words to the outside world the accreting solar system would have looked like a transient double star system! Quite a remarkable tidbit (if correct).
Solar
system bodies with (possible) subsurface oceans (2011) (2015)
Places in
the solar system (outside the earth) with liquid water are possible candidates
for life. Are any such places known? Not so long ago the answer was no.
Our moon and mars seemed completely dry, venus and mercury were too hot,
the outer planets were gas giants, their satellites were either dry or
if they held water it was in the form of ice like in comets, But things
have changed, a close look at the satellites of Jupiter and Saturn shows
water 'everywhere'. According to a recent article in NYT and Wikipedia
there are (at least) three bodies now thought to possibly contain liquid
water in the form of subsurface oceans: Saturn's small moon Enceladus,
Jupiter's moon Europa and Mars, and there is speculation that several other
of Jupiter's moons, like Callisto and Ganymede, (heated by gravity contractions)
may very well have a liquid subsurface ocean too.
-- Europa is unique because its ocean is believed to be in direct contact with its rocky interior, where conditions could be similar to those on Earth's biologically rich sea floor. In contrast, Jupiter's other large, icy moons, Ganymede and Callisto, are thought to contain "ocean sandwiches," where a liquid ocean exists between two layers of ice.
Enceladus and Europa
One candidate for
life, maybe the best candidate, is a small (300 miles) satellite of Saturn
called Enceladus. It has the highest albedo (reflectivity) of any body
in the solar system. It looks like clean white ice, much of it relatively
young, surface temperature 75 Kelvin. The Cassini spacecraft (in orbit
around Saturn) has made an amazing discovery (2008) of huge continuous
jets coming from its surface throwing ice particles into space. These ice
particles actually make up one of Saturn's diffuse rings within which Enceladus
orbits. While Enceladus in some ways is more interesting for the possibility
of life than Europa, it has a significant disadvantage in terms of exploration.
It's much further away than Europa, being a satellite of Saturn while Europa
is a satellite of Jupiter.
Current thinking is that the source of the ice jets of Enceladus is a large salty ocean beneath the surface. ("Enceladus, a Moon of Saturn, May Have Ocean Beneath Its Icy Surface" -- NYT headline (June 2011). Detail measurements by the Cassini spacecraft, in orbit for years around Saturn, has found Enceladus to be much hotter inside than expected. The source of all this internal heat is not well understood. The measured power outflow, much of it through the ice geysers, is 15.8 Gw (x2.5 Yellowstone power). This is x8 higher than the calculated power: gravitational squeezing @ 1.8 Gw and radioactive decay @ 0.3 Gw. However, it might be that since Enceladus is now known to wobble as it rotates (it's not completely spherical), its gravitational flexing is higher than was calculated.
-- In May 2011, NASA scientists at an Enceladus Focus Group Conference reported that Enceladus "is emerging as the most habitable spot beyond Earth in the Solar System for life as we know it".
-- "Enceladus has liquid water, organic carbon, nitrogen [in the form of ammonia], and an energy source," says Chris McKay, an astrobiologist at NASA's Ames Research Center in Moffett Field, California. Besides Earth, he says, "there is no other environment in the Solar System where we can make all those claims." No photosynthesis is possible, but raw materials that microbes on earth are able to live on are thought to be present: [hydrogen + carbon dioxide] (yielding methane) and acetylene (yielding ethanol and acetate).
-- Enceladus is one of only three outer solar system bodies (along with Jupiter's moon Io and Neptune's moon Triton) where active eruptions have been observed. (Wikipedia)
-- Interest in Enceladus was recently enhanced by a March 2015 report in Nature that plumes from Enceladus are hydrothermal, and that the water inside may in some spots be as hot as 90C. The assessment of water temperature is pretty indirect. Cassini going into orbit around Saturn detected submicron size 'dust' particle in the E ring and the E ring is known to come from plumes of Enceladus. These tiny dust particles are thought to be relatively pure silica, an atom of silicon plus two oxygen. Tests in the lab showed that to create particles like this water had to be quite basic and heated at least to 90C.
 .
.
Enceladus, small moon of Saturn
stripes (cracks) at bottom (in false color) near south
pole are the location of the ice (or thermal) plumes
(right) image released by NASA and JPL-Caltech on
supposed nature of the enceladus' thermal jets
Venus
Venus
barely rotates at all! A venus day (8.0 months) is longer than the
time it takes to orbit the sun (7.4 months), and it rotates backwards (retrograde).
Maybe its rotation was changed by a big hit early in its evolution. (I
at first though it was close to being pulled into sun synchronized rotation,
then I realized its not that close since it's going backwards.)
Greenhouse effect on Venus has grown huge increasing its surface temperature to 880F. Atmospheric pressure is 92x earth, equivalent to the pressure (about) 1 km down in the ocean on earth. The atmosphere is almost all CO2 (95%), much of it (probably) from volcanos. Venus clouds are sulfur dioxide/sulfuric acid and have lightning storms.
Venus has/had a huge number of volcanos (1,600 major volcanos have been counted), but curiously no evidence of shifting plates, which on earth are the major source of volcanos. Surface is relatively young with less meteor craters than earth. No lava flows ever seen, but some experts think volcanos may still be active. 70% of the planet surface is basalt (cooled magma). The surface looks like it completely 'turned over' about 500 mil years ago and then froze. This type of 'sticky' plate tectonics may be because venus lacks a plate lubricant, which on earth is subducted ocean water.
Galileo
calculates height of mountains on moon (10/09)
I am reading
Galileo's little book 'Sidereus Nuncius' that he rushed out in 1609 to
announce what he had found with his newly made x20 and x30 power telescopes
(really spyglasses). Looking at the light/dark terminator on the moon he
found it to be rough with separated light spots could often be seen on
the dark side and separated dark spots on the light side. He correctly
concluded he was seeing mountain tops in sunlight and deep valleys in shade,
exactly as can be seen on earth at sunrise in the mountains.
But interestingly he points out he has been able to use this simple observation to calculate the heights of the mountains on the moon. He finds some isolated light spots are as much as 1/20 of the diameter of the moon away from the terminator. He knows the ratio of the moon's diameter to the earth's is as 2 to 7, and the earth's diameter is about 7,000 miles making the moon's diameter 2,000 miles. (Footnote says that sizes of the earth and moon had been known to great accuracy since antiquity.) Drawing a triangle from the center of the moon to the terminator and light spot, the short triangle side of the triangle to the radius is 100 miles to 1,000 miles. Using pythagorean theorem he calculates the length of the slightly longer triangle side (to the light spot):
sqrt{100^2 +1,000^2} = 1,005 miles
1,005 miles - 1,000 mile radius = 5 miles
Subtracting the longer triangle side from the 1,000 mile moon radius give the (absolute) moon mountain height of 5 miles. Pretty neat!
Liquid on
surface of Titan
Titan, the
largest moon of saturn, is unique in the solar system in that there is
good evidence that are liquid lakes on its surface. The liquid on titan
is methane. Newly cleaned up images (despeckled) from the Cassini spacecraft
give a nice view of the shore line. Titan has a thick visually opaque atmosphere,
so the image below has been obtained from radar images.
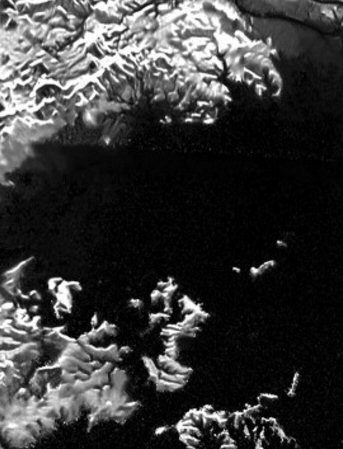
radar image of titan's liquid lake shore line
Earth's interior (5/10)
An interesting
paper in Scientific American shows an important new layer (blue) of the
earth's interior, which has only recently been discovered and confirmed.
Previously puzzling reflections from seismic data at the bottom of the
mantle just above the core are now understood to be a 300 km layer of a
previously unknown high temp/high pressure phase (atomic rearrangement)
of the mineral perovskite. This new quasi-mineral is a much better heat
conductor than the rest of mantle, and computer models show it significantly
affects the interior cooling timeline of the planet, and perhaps via the
magnetic field its biology too. The different temperature timeline of the
core may mean that the earth's magnetic field started earlier than previously
thought, thus via its shielding of the solar wind affect may have affected
life on the surface.
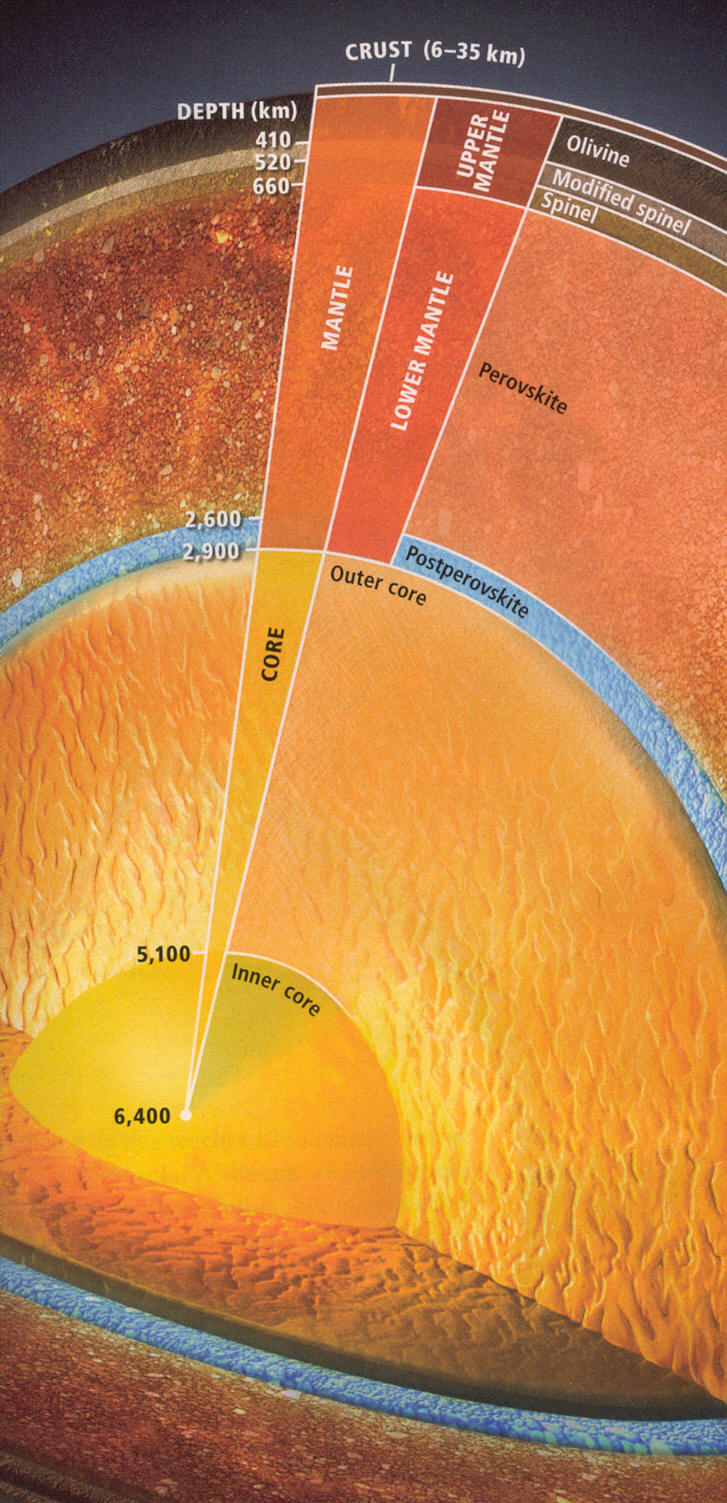
great drawing of earth's interior
blue layer is new, phase of perovskite called postperovskite
(scan from Scientific American May 2010 edition)
The inner and outer metal core of earth is mostly iron and nickel. The inner core is solid, while the outer core is liquid and the source of the magnetic field. The numbers on the drawing show the core/mantle boundary is at slightly more than half the radius of the earth [(6400-2900)/6400 = 0.55]. By volume the core is about 16% of the earth with the mantle the remaining 84%. Temperature at the core/mantle boundary is about 4,300K with the temperature in inner core reaching about 5,700K, a little hotter than the surface of the sun. The solid core the earth now has can be viewed as a 'freezing out' that has occured as the previously fully molten core has slowly cooled over the lifetime of the earth with the cooling rate estimated to be about 100C/billion years.
The mantle is a highly viscous silicate, mostly oxygen, magnesium, and silicon (magnesium silicate MgSiO3), a mineral called perovskite. The blue layer is a slightly denser atomic rearrangement of the mineral perovskite, called postperovskite. Perovskite was thought to have an optimum atomic arrangement, so the actual creation of a slightly more compact phase of perovskite at the known density and temperature at the bottom of the mantle in a diamond anvil was a real breakthrough. The pressure was so high their diamond anvils kept exploding. Its creation came only after a Japanese team improved the diamond anvil to allow it to go about 50% higher in pressure.
Weighing the earth
Feynman points
out (in his book 'Character of Natural Law') that until there was a lab
measurement of the gravitational attraction between objects no one knew
the value of the gravitation constant 'G'. From Newton's time it was known
that objects on the surface of earth we feel a pull of gravity described
by:
F (gravity) = GmM/r^2
where
G = gravitational constant
m = mass of object
M = mass of earth
r = radius of earth
In the the late 1700's size of the earth was pretty well known, and of course the 'weight' of an object was easily measured. This meant that the product 'GM' was known, but since the mass (M) of earth (or equivalently its density) was not known, no one could separate out G.
The first measurement of gravity between objects in the lab was made in 1798 by Henry Cavendish (using a design by John Mitchell) using a torsional balance. He hung a horizontal arm with two small (1.6 lb = 0.73 kg) balls attached to the ends by a long very, very fine quart wire connected in the middle of the arm. The apparatus was free to rotate by twisting the wire. The wire when twisted exerted a very, very weak restoring force (approx) linear with angle (k x theta), basically its a rotational spring. The spring constant (k) was found by measured the spring's resonance. Cavendish placed large heavy balls (348 lb = 158 kg) near (9 in = 0.23 meter) the small balls on the arm and measured the resulting displacement angle of his balance, which since 'k' was known gave the gravitational force between the small balls (on the arm) and the large balls.
Cavendish then argued that the ratio of his measured (twisty) force on a small ball to its gravity force (its weight) must be equal to the ratio of the weight (mass) of his large ball to the weight (mass) of the earth adjusted for the separation distances squared. In other words:
158 kg/(0.23 m) ^2
(measured
twist force/0.73 kg of force) = ----------------------------
mass earth/(6,360 km)^2
The mass of earth is 6 x 10^24 kg, so the force Cavendish must have measured
158 kg/(0.23 m) ^2
(measured
twist force/0.73 kg of force) = -------------------------------
6 x 10^24 kg/(6.4 x 10^6 m)^2
3.0 x 10^3
= ---------------
1.5 x 10^11
= 2 x 10^-8
In other words Cavendish (in 1798) had to measure a force that was about one in 100 million (10^-8) of the weight of his 1.6 lb balls. And amazingly his experiment must have been good to about one part in 10 billion (10^-10) because his calculated earth weight came out to be accurate to about 1%!
Wikipedia says Cavendish built his apparatus in a 10 foot wooden box 2 feet thick (!) to keep out air currents. The period of the resonance was about 7 minutes. The large balls caused a 4 mm deflection of his rod, which with the aid of vernier scales and a telescope he was able to read to a resolution of 0.25 mm (one part in 16). His experiment was repeated by others several times, but it took almost 100 years before anyone improved on his accuracy.
Density of the earth was found by lab measurements of gravity to be 5.5 g/cm^3. This is 5.5 times higher than water (1 g/cm^3) and about twice the density of most surface rocks, which run between 1.7 to 3 g/cm^3 (granite is 2.8 g/cm^3). But iron is 7.9 g/cm^3 indicating that it is very likely that a substantial part of the earth inside is made of iron.Evidence for a 9th planet beyond the Kuiper Belt (spring 2016)Check earth density = 5.97 x 10^24 kg/ (pi/6) (8 r^3)
= 5.97 x 10^24 kg/[4.189 x (6.37 x 10^6 m)^3]
= 5.51 x 10^-3 x 10^6 kg/m^3
= 5.51 x 10^3 kg/m^3
= 5.51 g/cm^3 yup, checks
The proposed explanation for these aligned orbits is a massive planet extending the other way from the sun. What Brown and Batygin did was a computer simulation playing with size and orbit of a proposed 9th planet to see if it could cause the kuiper belt orbits that are seen, and they found a match. This is where the prediction of the orbit and mass of the proposed 9th planet comes from. Unfortunately this simulation does not give any information on where in the orbit the planet might be now, so there's a lot of places to look. Brown has reportedly got time on a very large telescope to start looking for the 9th planet, and he is encouraging other astronomers to look too.
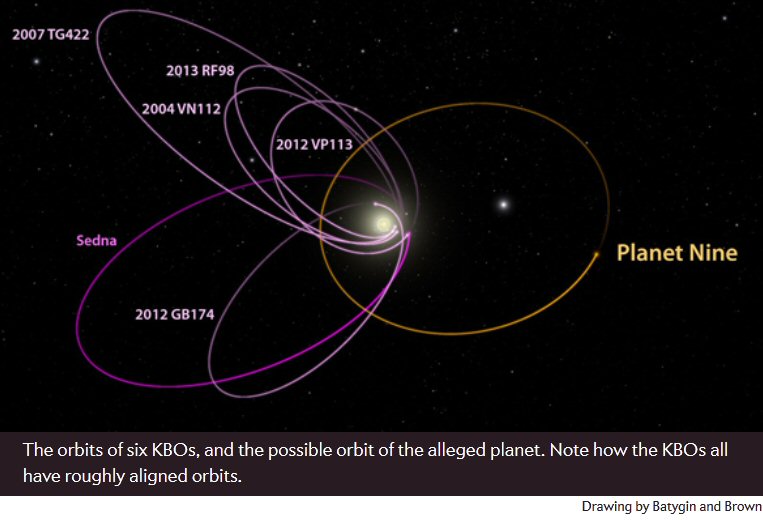
KBO = Kuiper Belt Object
This proposed 9th planet is far, far out. It's closest approach to the sun being 200 AU, which is about x7 further out than neptune and x4 further out than the furthest distance of pluto. The furthest distance of it highly elliptical orbit is less well known and could be between 500 and 1,200 AU. The planet's estimated mass is x10 earths, about 60% of neptune. Time to orbit the sun is 20,000 years. The astronomer's say because it is big and affecting the orbits of other bodies, if it exists. it is definitely a planet. For reference, the furthest out planet Neptune is at 30 AU, and former 9th planet Pluto varies between 30 and 50 AU.
Brown (50, senior observational astronomer) and Batygin (29, computer modeler) are astronomers at CalTech. A French peer reviewer of their paper says they make a very solid argument, and he is convinced the planet exists. Outside astronomers, like Slate's excellent astronomer columnist Plil Plait (friend of Browns) say this is fairly strong evidence for a 9th planet. It fits too with what is known of the formation of the solar system where it is presumed that some planetary size objects were thrown into the sun or out of the solar system (or just maybe far, far out!) by the larger planets jupiter (x317 earths) and saturn (x95 earths). There's an additional data point too. Something interesting fell out of the simulation, the orbits of some affected kuiper belt objects should tilt up strongly out of the plane of the solar system. And it turns out that a handful of kuiper belt objects with just this sort of unexplained oddball orbits have been found, and they are just where the simulation says they should be. Brown says when this was found that's when he became convinced the 9th planet was real. Caltech has released a 3 min video of Brown and Batygin talking about the ninth planet:
https://www.youtube.com/watch?v=6poHQ2h00ZA
Pluto
and large kuiper belt objects (4/26/16)
In the last
15 years or so a bunch of large kuiper belt objects have been discovered,
most by a team led by Caltech astronomer Mike Brown. I just read Caltech
astronomer Mike Brown's fun book, 'How I Killed Pluto and Why it had it
Coming', where he describes the search, and the controversy over whether
a Spanish astronomer really beat him out (by a day) on Haumea. The
press interest (several front page stories in NYT including one yesterday
when Makemake was found to have a moon) is always on whether newly found
kuiper belt objects are bigger than pluto.
No kuiper belt object has been found has been definitely 'bigger' than pluto, but Eris is virtually the same size and is 28% heavier than pluto. The size of pluto is now very well known since about six months ago a spacecraft (New Horizons) flew by it taking a bunch of hires photos. IAU (International Astronomical Union) currently recognizes only five 'dwarf planets: Pluto, Eris, Makemake, Haumea, and Ceres. Ceres is the largest object in the asteroid belt. The only asteroid belt object to be rounded by its gravity and is estimated to contain 1/3rd the mass of the whole asteroid belt.
For perspectivePluto dwarf planet 1,186 km (radius) 29 - 49 AU 248 yr .177 moon (1.303 x 10^22 kg)
Eris dwarf planet 1,163 km (radius) 39 - 97 AU 558 yr .23 moon
Makemake dwarf planet 715 km (radius) 38 - 52 AU 309 yr ---
Haumea dwarf planet 575 - 718 km (radius) 35 - 51 AU 294 yr .054 moon
Quaoar dwarf planet? 555 km (radius) 42 - 45 AU 286 yr .019 moon
Sedna minor planet --- 76 - 936 AU 11,400 yr ---Ceres dwarf planet 473 km (radius) 2.5 - 3 AU 4.6 yr .0125 moon
Brown says that Sedna is very interesting because it is very distant and very eccentric with the longest known orbital period (11,400 years). Notice Sedna shows up in the figure above as it is one of reasons a 9th planet is suspected.
Dwarf planet --- Spherical celestial body revolving about the sun, similar to a planet but not large enough to gravitationally clear its orbital region of most or all other celestial bodies. For example pluto.
Solar system formation
(5/1/16)
There's
an interesting article in May 2016 Scientific American that provides new
perspective on how the present arrangement of planets in the solar system
came to be. A huge number of exosolar planets are now known, the
article says the Kepler mission has detected thousands. Astronomers are
coming to realize that exosolar planetary systems that look like the solar
system are 'relatively rare'. In what ways? For one thing the average planetary
system has one or more super earths (planet a few times larger than earth)
close in with periods of less than 100 days. Giant planets like Jupiter
and Saturn are found in only 10% of planetary systems and fewer still with
'sedate
nearly circular orbits. From an outside perspective one thing quite unusual
about the solar system is nothing orbits in close. There is no known
object orbiting inside mercury with its 88 day orbit, and for a planet
mercury is tiny, only a little bigger than our moon (40% larger radius
and weighing 4.5 moons).
(5/2/16)The article points out that with this outside perspective good progress has been made by solar system computer modelers in the last 15 years. They can explain how close in super earths would have disappeared and why jupiter and saturn are now so far out in nearly circular orbits.
Earth size planets with orbital periods of 1 - 2 days
A paper in Nature today describes two earth size planets that have been found around a tiny dwarf star that is very close (40 light years) to us. These are the first exosolar planets ever found around such a small star. This star is described as an ultracool dwarf, 8% of the sun's mass, and only 5% of the sun's luminosity. 8% solar mass is about as low as the mass can be for a star that supports fusion. The planets were found by dimming using an infrared (?) TRAPPIST telescope. The interesting thing is that they are so close to the star that their orbital periods are 1.5 days and 2.4 days. One researcher said the scale of this system is more like jupiter and its moons, since the star itself is barely bigger than jupiter.The planets are so close to us and the star is so dim that it should be possible to look at their atmospheres for molecules that might indicate the presence of life.
Grand tack
The modelers
describe inward then outward movement of jupiter and saturn as the 'grand
tack' (sailboat term). Jupiter drifts in and saturn follows and together
they start clearing a large gap in the disk. If jupiter had, say, moved
in as far as mars orbit, it would have messed up all the orbits of inside
terrestrials that had formed including potential super earths causing lots
of collisions. The simulations suggest that drag through the gas would
have caused all the collided stuff to lose energy (as heat) and go into
a death spirals and in 100k years they all fell into the sun. This explains
why the solar system is 'hollowed out' with nothing but (small) mercury
orbiting below 100 days. And also explains why mars is small.
At some point saturn catches up with jupiter they synchronize orbits (3:2) and are even more effective in clearing a gap. The article says planets with synchronized orbits can exchange momentum and energy back and forth, so they act on the neighbourhood as one big plant. This changes the way they interact with the gas in the disk and counter-intuitively after moving in (snowplowing stuff ahead of them), they reverse course and begin to move out.
Later when jupiter/saturn pair moves out they synchronize for a while with another synchronous pair uranus/nepture. But this four way synchronous system is not stable and eventually one breaks away, and so the gas giant orbits go chaotic, beginning what is called the 'late heavy bombardment' (3.8 to 4.1 billion years ago), where possibly one gas giant may have been thrown out. What stabilizes the gas giant orbits is interactions with icy planetesimals, which when they get close are ejected, lowering orbital energy of the gas giants and making their orbits more circular. The four terrestrial planets form hundreds of millions of years after jupiter has moved out from the remaining narrow ring of dust and rock.
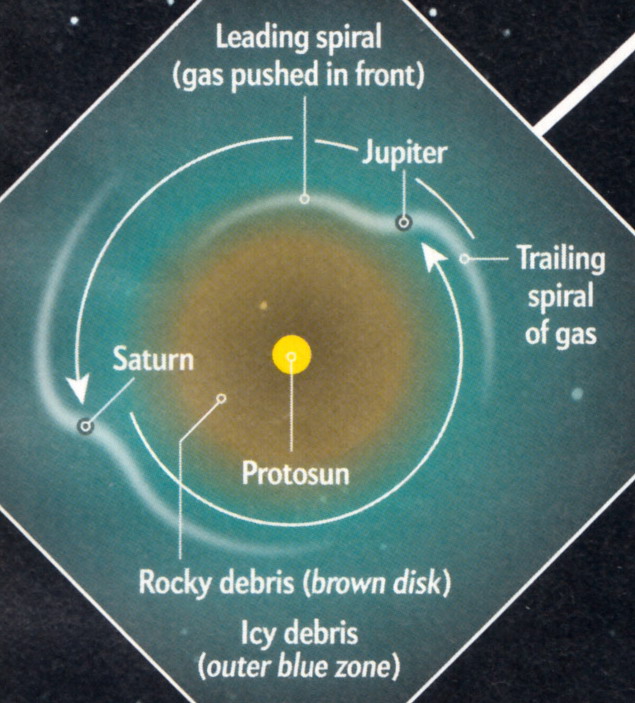 .
. 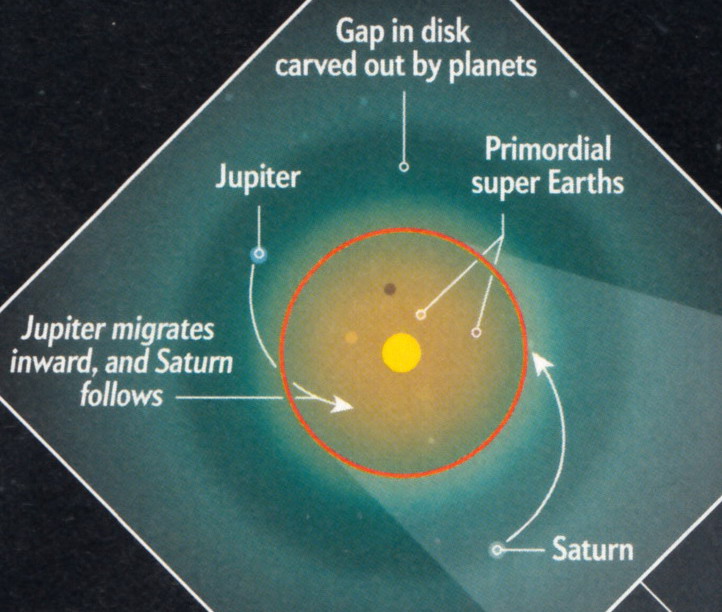 .
. 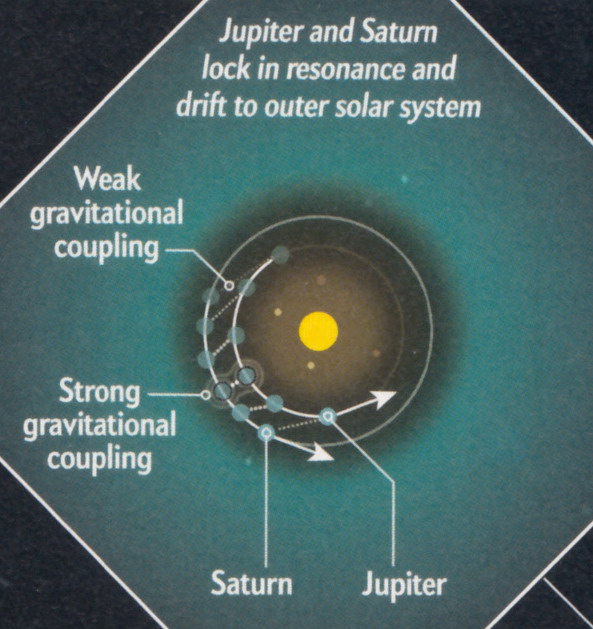
jupiter and saturn drift in, clear a large gap in
disk, and after they lock in resonance they drift out
scans of Scientific American article figures
In other words these models have the disk first forming the present four gas giant planets with an early generation of terrestrial planets, including possibly several giant earths. When jupiter and saturn drift in they screw up the orbits of these first generation terrestrials, which are all destroyed as they collide with each other, lose energy and momentum to the gas and dust of the disk causing them to fall into the sun. After saturn and jupiter synchronize they reverse course and drift out causing all the gas giant orbits to go chaotic as they approach uranus and neptune which are also a synchronized pair. Over time interactions with icy planetesimals coming in from the kuiper belt stabilize the orbits of gas giant planets. The present four terrestrial planet form much later from the remaining rock in the inner solar system.
Transient of Mercury
(May 2016)
Another transient
of mercury showing how small it really is. Nasa photo, likely taken from
a satellite.

Milky Way as seen from grand canyon rim
Image of Milky
Way from Grand Canyon rim taken during an eight night star party in the
park. Light pollution from three major cities can bee seen in the distance.

Milky Way as seen from Cape Royal on the North Rim
of the Grand Canyon.
Three urban areas emanate haloes of light, from left
to right: Flagstaff, Ariz., Phoenix and Prescott, Ariz., and Las Vegas.
Credit: Jeremy White
Rock
from outside the solar system (oct 2017)
Astronomers
in fall 2017 have discovered a large rock (1,200 ft) moving very fast in
a very unusual orbit. The orbits of all the planets, asteroid belt, kuiper
belt (pluto) are very regular. They are all in the same plane, all rotate
in the same direction and while technically ellipses they are nearly circular.
As the image below shows, this object is coming in nearly perpendicular to the solar system plane and at such a high speed that its orbit is an open ended hyperbola. The astronomers say this orbit shows convincingly that this object has come into the solar system from outer space, and this is the first time such an object has ever been observed.

------------------------------------------------------------------------------------------------------------------------------------------------------
Is the sun
an average star? (4/15)
Ans: No. The
sun is much bigger and puts out much more energy the average star. On a
recent Nova show about the Kepler Observatory, which is looking for planets
using light dimming of the star by the planet (transients), an astronomer
on camera says in school he was taught the sun was an average star,
but he says that was an absolute lie. Three quarters of all stars in our
galaxy are M type dwarfs (more commonly called red dwarfs), and while they
vary in size and energy, they typically put out only a tiny fraction of
the energy put out by the sun. He says a red dwarf with about 10% the mass
of the sun and a radius 15% that of the sun will output only about one
thousandth
of the energy of the sun (technically its luminosity is only about 0.1%
of the sun).
For the Kepler planet hunters, who are looking hard for earth like planets, this is a good thing. A transient of an earth size planet across a red dwarf disk with 15% the diameter of the sun will have a light dip x44 times higher than for a transient of the same size planet across the sun because surface area of the red dwarf star is x44 times smaller than the sun [44 = (1/0.15)^2]. In other words a 0.008% light reduction of an earth like planet across the sun will be a 0.36% light dip across a red dwarf, much easier for the Kepler to see.
What
fraction of the sun is helium?
The pp chain,
which is the dominate fusion reaction in the sun, has very low efficiency
and only converts about 0.7% of hydrogen mass (proton mass) to helium.
Obviously the percent of original hydrgen converted helium over the lifetime
of the sun could be estimated by knowing the mass of the sun and solar
power output. (I do the calculation below) Another way to estimate it is
that the sun is now about halfway through its ten billion year main sequence
liftetime, so it must have converted about half of its original hydrogen
that is hot enough to fuse. But estimates are that only about 10% of the
hydrogen of the sun is deep enough in the core so it can get hot enough
to participate in fusion reactions. This would imply that roughly 5% of
the original hydrogen mass of the sun has at this point been converted
to helium. And in round numbers if the sun was originally about 75% hydrogen,
then the helium created by fusion would be 3.75% the mass of the sun.
Using numbers in Wikipedia 'Sun' we can calculate the amount of hydrogen converted to helium over the lifetime of the sun and we get numbers in the same ballpark as above.
sun's mass
333,000 earth mass
sun has converted to energy over its lifetime
100 earth mass (obviously an approx
number)
est fraction of sun's mass converted to helium
(100 / 0.007)/330,000
= 14,286/333,000
= 4.3%
Helium in universe and change with time
The amount of helium
in the universe and how it has changed with time is hard to pin down. Wikipedia
(helium) says that 24% of the universe now is helium, but how much
of this was created in the big bang and how much in stars is not broken
out.
Wikipedia (Abundance of elements in the universe) gives the current percentage for helium in the Milky Way (which is nearly all in the sun): 24.0% helium, 73.9% hydrogen and 1.5% oxygen + carbon.Hyperphysics has a section on hydrogen-helium ratio created in the big bang and their post big bang numbers are 26% helium and 74% hydrogen. Nearly all references put the mass of all other elements in the universe combined now at about 2% (with the bulk of this just oxygen and carbon).
It's difficult to figure how much helium has been made in stars since the big bang, and more difficult still to estimate net the change in helium since the big bang. Wikipedia (helium) just says "large amounts" of helium are being created in stars. However, it does seem to me the amount of helium that has been destroyed (in high mass stars and supernovae) can be no higher than 2%, since this is the mass of all higher elements combined.
Where the hydrogen
is
How much helium
has been created (in stars) depends on where the hydrogen is. Hydrogen
in molecular clouds is unchanged, and hydrogen in low mass stars, which
have lifetimes far in excess the present age of the universe, is nearly
all still there too, so their contribution to new helium is virtually zero.
High mass, short lifetime stars might be able to fuse a significant fraction of their hydrogen to helium, only later to destroy a fraction of it (stars end up looking like onions with shells of different elements prior to going supernovae) when helium fusion starts and later some stars go supernova, so on balance these stars may only add a modest amount net to the universe's helium. It might seem that stars like our sun, and sun like stars born earlier, are the main creators of new helium. This may be true for now and based on the previous calculation we can roughly bound this helium creation at 4% - 8%. But Wikipedia (helium flash) points out that low to medium mass stars, 0.5 to 2.25 solar mass, will in the future go on to helium burning, destroying much of their helium in a 'flash' (essentially an explosion lasting a few seconds).
Calculation
of helium created in sun during its lifetime
Here's my
calculation of the fraction of the sun's mass that been converted from
hydrogen to helium during its 4.57 billion year lifetime. I began with
solar numbers from Nasa's
sun page (Wikipedia's (sun) uses this page as a reference). And I put
in two correction factors: 0.85 since I read the sun has brightened about
30% over its lifetime, and 1.03, since I read that about 3% of the sun's
output is in the form of neutrinos. (My guess is that Nasa's sun's energy
output is essentially a measured value, which would mean, of course,
that it does not inlude the neutrino energy.)
Mass of sun
1.99 x 10^30 kg
(earth's mass = 5.97 x 10^24 kg)
Power output of sun
3.85 x 10^26 watts or (joules/sec)
Mass conversion rate of sun
4.30 x 10^9 kg/sec
Sun's age
4.57 x 10^9 years
Sec in a year
3.156 x 10^7 sec/yr (3,600 sec/hr x 24 hr
x 365.25 days/yr)
Sun's lifetime (sec)
1.442 x 10^17 sec (3.156 x 10^7 sec/yr
x 4.57 x 10^9 yr)
Sun's lifetime energy output
(0.85 x 1.03) x 3.85 x 10^26 joules/sec x 1.442 x 10^17 sec
= 4.86 x 10^43 joules
Sun's lifetime energy mass loss
4.86 x 10^43 joules/(2.99 x 10^8 m/sec)^2
(m = E/c^2)
= 5.44 x 10^26 kg
(91 earth masses)
Hydrogen converted to helium
5.44 x 10^26 kg mass lost/.007 pp chain efficiency
= 7.77 x 10^28 kg
Fraction of sun's mass converted
to helium
7.77 x 10^28 kg hydrogen to helium/1.99 x 10^30 kg mass of sun
= 3.90 x 10^-2 or (3.9%)
Check
The numbers
check out well. Wikipedia (sun) says about 100 earths have been consumed
for energy production over the life of the sun, and I get 91, which would
be close to a 100 if my correction factor for brightening of the sun were
not included. The final result of 3.9% of the sun's mass converted to helium
is close to what approximate calculations yielded.
Original
composition of the sun
I can now
figure the sun's original composition, which I have not been able to find
anywhere in spite of a lot of searching. Wikipedia gives the percent of
helium in the sun now at 24%. My calculation above gives that 3.9%
of the sun's (total) mass has been converted over its lifetime from hydrogen
to helium. This must mean that helium made up about 20% of the original
gas cloud that condensed to form the sun, an interesting number because
it is considerably below the 26% or so helium (Hyperphysics) that
is calculated to have resulted from the big bang. An interesting minor
mystery that seems to get no attention.
Wikipedias (sun) has the sun's metallicity at 0.0122 (or 1.22%), so factoring this in I get the original composition of the sun when it formed 4.6 billion years ago to have been:
hydrogen
77.7%
helium
21.1%
(24% now from Wikipedia - 3.9% created from hydrogen)
all other elements
1.2%
(mostly oxygen and carbon)
Why
do we see the sun as having a surface?
If the sun
is a big ball of gas that gradually thins out into an 'atmosphere', why
don't we see the sun's edges as fuzzy? Good question. The answer lies in
the properties of plasmas. If gas is heated hot enough, it turns
into a plasma. A plasma is a state of matter hot enough so that some (or
all) of its electrons are stripped from the nuclei and move around freely.
As the gas becomes a plasma, it changes from being transparent to light
to being opaque. The flame of a candle, which is opaque, is an example
of a low temperature plasma.
Plasmas are opaque because free electrons absorb light much more strongly than ordinary matter. The sun inside is all plasma, but as distance from the core increases the temperature and pressure drop. At some point (zone) the temperature and pressure get low enough so that the plasma dies, meaning all (or most) of the free electrons get captured by nuclei becoming normal atoms, and a gas made up of normal atoms is largely transparent. This is the surface we see.
We see as the 'surface' of the sun the top of the outermost plasma zone. Since the transition from plasma to non-plasma occurs quickly, in about 100 miles or 0.01% of the diameter of the sun, we see the sun as having a sharp surface. This zone of the sun where the plasma dies and the atmosphere becomes transparent allowing photons to stream out to hit earth is called the photosphere. It's density is quite low, only 1% of the density of air on earth (at sea level).
Sun's internal zones
The core
extends from the center of the sun about one-fourth of the way to the surface.
The core has about 2 percent of the sun's volume, but it contains almost
half the sun's mass. Its maximum temperature is over 15 million Kelvins.
Its density reaches 150 grams per cubic centimeter, nearly 15 times the
density of lead. Almost all the fusion in the sun takes place in the core.
The core is now half helium.
Surrounding the core is a huge spherical shell known as the radiative zone. The outer boundary of this zone is 70 percent of the way to the solar surface. The radiative zone makes up 32 percent of the sun's volume and 48 percent of its mass. The radiative zone gets its name from the fact that energy travels through it mainly by radiation
The highest level of the solar interior, the convection zone, extends from the radiative zone to the sun's surface. This zone consists of the "boiling" convection cells. It makes up about 66 percent of the sun's volume but only slightly more than 2 percent of its mass. At the top of the zone, the density is near zero, and the temperature is about 5800 K. The convection cells "boil" to the surface because photons that spread outward from the radiative zone heat them.
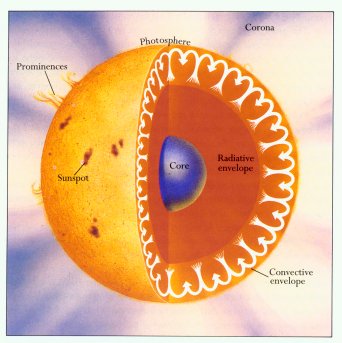
Sun entry on Univ of Illinois Star site (http://www.astro.uiuc.edu/~kaler/sow/sun.html)
Sun's
surface or light emitting zone
Most of the
light that we see comes from lowest 100 miles of the 300 mile thick photosphere,
which is lowest part of the sun's atmosphere. Astronomers often refer to
this part of the photosphere as the sun's surface. At the bottom
of the photosphere, the temperature is 6400 K, while it is 4400 K at the
top. The sun emits light pretty much like a black body with a peak black
body temperature of 5,780 K. This produces a broad spectrum of light with
most of the energy in the human visible range (400 to 700 nm). As the light
passes through the upper regions of the sun's atmosphere some narrow frequencies
of light are absorbed. The result is that the sunlight we see has a series
of narrow black lines in it corresponding to the absorption/emission spectra
of the elements in the atmosphere..
The photosphere consists of numerous granules, which are the tops of granulation cells. A typical granule exists for 15 to 20 minutes. The average density of the photosphere is less than one-millionth of a gram per cubic centimeter. This may seem to be an extremely low density, but there are tens of trillions to hundreds of trillions of individual particles in each cubic centimeter. The 'boiling like' granular structure of the sun's visible surface is quite spectacular in some pictures and videos of the sun.
Sun's motion
The sun revolves
around the galactic center once about every 250 million years. Note this
is quite slow relative to the lifetime of the sun and galaxy. Since the
sun is about 4.6 billion years old, it has (probably) only made about 18
revolutions about the galactic center!
Sun's fuel burning
The sun is
now burning hydrogen, and it has enough hydrogen to do this for about another
5 billion years. When the core of a star runs out of hydrogen, the core
begins to contract. This releases gravitational energy that heats the core
hotter and hotter and causes the outer layers of an intermediate mass star
(like the sun) to hugely expand turning the star into a red giant. (In
a sense) the sun will expand all the way out to the earth's orbit (bye
earth!).
When the core gets super hot, helium burning starts (using the triple alpha process), and because the sun is an intermediate mass star, helium burning will start explosively. This explosion is called a helium flash, and it can burn 60-80% of the helium in the core in a few minutes! The helium burning starts explosively because the density of helium in the core (as fusion starts) is controlled by principally by electron degeneracy pressure (electron-to-electron repulsion), which is not temperature sensitive.
The sun is not large enough to burn any element above helium. When fusion stops, the sun will shrink (which heats it) to become hot white dwarf, and then it will very slowly cool ending as a black dwarf.
Helium flash
The triple-alpha
process (helium burning to carbon) is strongly dependent on temperature
and density. The energy released by the reaction is approximately proportional
to the temperature to the 30th power (wow!), and the density squared. Contrast
this to the PP chain (hydrogen burning) which produces energy at a rate
proportional to the fourth power of temperature and directly with density.
Higher temperatures in a star core result in a higher outward thermal pressure, and if the core (responding to this pressure) expands (lowering density and temperature), the fusion reaction rate slows. This is the key feedback mechanism in stars that stabilizes their fusion reactions, preventing them from blowing up like bombs. But when electron degeneracy pressure, which is purely a function of density, dominates over thermal pressure, which is proportional to the product of density and temperature, the total pressure is only weakly dependent on temperature. What this means is that the normal star fusion stabilizing feedback mechanism is broken.
Thus, once the temperature reaches 100–200 MK and helium fusion begins, the temperature rapidly increases, which further increases the helium fusion rate and expands the reaction region, but the (over all) pressure does not increase (since electron degeneracy pressure is dominant), so the core doesn't expand and provide stabilizing cooling. This runaway reaction quickly climbs to about 100 billion times the star's normal energy production (for a few seconds) until the increased temperature again renders thermal pressure dominant, eliminating the degeneracy.
Note a helium flash in a red giant is related to a type Ia supernova. In a type Ia supernova falling mass on a white dwarf star starts fusion going, and because the star size is controlled by electron degeneracy, the normal thermal expansion feedback mechanism to control fusion is missing, leading to uncontrolled temperature increases, a huge supernova explosion. Wikipedia says, "Within a few seconds a substantial fraction of the matter (much of it carbon and oxygen) in the white dwarf undergoes nuclear fusion, releasing 1- 2 x 10^44 joules."
http://www.nasa.gov/worldbook/sun_worldbook.html
Future
of the sun -- main sequence => red giant => white dwarf/planetary nebulae
Our sun is
a large, G2, yellow, main sequence, hydrogen burning star, and it will,
along with 95% - 97% of all stars in our galaxy, eventually expand hugely
to a red giant (as helium burning starts), then shrink hugely to a white
dwarf (as all fusion stops), and in the transition from red giant to white
dwarf about 40% of the mass is thrown off in the form of a planetary
nebulae.
A planetary nebulae is the gaseous and dusty material expelled by a red giant as fusion stops and it exposes the dense, hot, tiny white dwarf star at its core. A white dwarf, as long as its mass is less than 1.4 solar mass (Chandrasekhar limit), is prevented from collapse by electron degeneracy pressure. The ejected material often forms beautiful concentric sets of spherical bubbles or halos around the core star. For a few thousand years each nebula brightens and turns from red to green. After 10,000 years or so, the growing nebula will expand and fade into the background of galactic gas. Famous planetary nebula have popular names like: Cat's Eye, Ring, Eye of Jupiter, Eskimo, Saturn, and Blue Snowball.
Eskimo planetary nebula (NGC 2392) about 3,000 ly
distant. Age estimated to be about 1,000 years. (Hubble photo, Wikipedia)
I stumbled on the curious fact that the density of nebula (like above) is very low; far lower than what can be achieved in the best vacuum on earth. Nebula density (main body) runs about 5,000 particles/cm^3, whereas the best vacuum on earth is 10^-13 torr, or 200,000 particles/cm^3, x40 higher than the nebula density.The other 3%-5% of stars -- that is, those born with masses more than eight times larger than our Sun -- end their lives as supernovae.-- Particle density of the Earth's atmosphere at sea level is 10^19/cm^3
Five billion years from now the hydrogen fuel our sun is now burning will be depleted. At that time the outer layers of the sun will expand to form a huge red giant star. As a red giant the sun will be so bloated that its outer layers will envelope Mercury and Venus. From earth the huge bright red Sun will fill half the sky. The oceans will boil and evaporate into space, along with the atmosphere.
The helium won't last long - less than a few hundred million years. The solar core, which will consist of unburnable carbon and oxygen, will shrink quickly (a few thousand years) down to the size of the earth, packing about half the the mass of the present sun into this small volume. The shrinking of the core will make it white hot and very dense turning the sun into a white dwarf star. Even though there is no fusion in a white dwarf star, it is so hot and has such a small surface area that it takes a very long time (> 10 billion years) to cool off, slowly changing from a white dwarf to an orange dwarf to a red dwarf.
The stellar evolution picture above is somewhat simplified. Here is a more detailed picture from Wikipedia about the white dwarf in the binary star system Pegasi 150 light years away:
"As its hydrogen fuel at the core became consumed, this star evolved into a red giant. The inner core contracted until hydrogen burning commenced in a shell surrounding the helium core. To compensate for the temperature increase, the outer envelope expanded to many times the radius it possessed as a main sequence star.When the core reached a temperature and density where helium could start to undergo fusion, this star contracted and became what is termed a horizontal branch star. That is, it belonged to a group of stars that fall upon a roughly horizontal line on the H-R diagram. The fusion of helium formed an inert core of carbon and oxygen. When helium was exhausted in the core, a helium burning shell formed in addition to the hydrogen burning one and the star moved to what astronomers term the asymptotic giant branch, or AGB. (This is a track leading to the upper-right corner of the H-R diagram.) If the star had sufficient mass, in time this core too could initiate fusion of carbon into oxygen, with neon and magnesium as by-products."

Sun's density
and black holes
The sun and
jupiter have about the same average density, which is lower than
that of earth (25% of earth). 109 earths can be lined up across the disk
of the sun.
To get a feeling
for the incredible density of (stellar) black holes, the sun's mass would
need to be shrunk down to a diameter of 3-4 miles for it to be a black
hole! The schwarzschild radius for one solar mass. The density of black
holes varies a lot. Wikipedia says the schwarzschild radius is proportional
to mass (very famous, very simple characteristic of black holes), so x2
mass means x8 volume, thus 1/4th the density. Clearly black hole density
goes inversely as the square of its mass. Wikipedia (schwarzschild radius)
gives the density a black hole with all the mass of the milky way galaxy
as 10^-8 g/cm^3, a one solar mass black hole as 10^16 g/cm^3 (round numbers),
an earth mass black hole as 10^27 g/cm^3 (1" dia), and the smallest possible
black hole, the so-called planck particle (10^-8 kg) has a density of 10^91
g/cm^3.
------------------------------------------------------------------------------------------------------------------------------------------------------
Smallest
possible black hole (1/6/16)
I came across
an extraordinary statement in a 2008 book, 'The Black Hole War', by Leonard
Susskind, one of the world's great theoretical physicists and a great writer.
It's a linking of quantum mechanics, gravity and black holes. He says (p114)
planck length, time, and mass are the size, half-life, and mass of the
smallest possible black hole. Wow.
Half life of min-black holeWikipedia has a page on this minimum size black hole calling it the 'planck particle'. It begins with this somewhat more technical description: "A Planck particle, named after physicist Max Planck, is a hypothetical particle defined as a tiny black hole whose Compton wavelength is equal to its Schwarzschild radius. Its mass is thus approximately the Planck mass, and its Compton wavelength and Schwarzschild radius are about the Planck length." While it would be super tiny compared to a proton, 10^20 times smaller in dia(!), it would be super heavy weighing 10^19 more than a proton.
Susskind (above) says the half-life of a minimum size black hole is planck time. Planck time is incredibly short (10^-35 sec), so these are pretty much virtual particles. When black holes were understood to have entropy and temperature, their temperature came out to be inversely proportional to mass. So a teeny tiny low mass black hole like a planck mass black hole is incredibly hot, that's why its lifetime is so short. It radiates away all its energy (its mass) in planck time, the black hole can be said to 'evaporate'.
Now this is super theoretical. Planck length is an incredibly tiny dimension about 10^-35 m, whereas astronomically the smallest black holes ever found have dia measured in miles. NASA recently announced the smallest black detected has 3.8 solar mass with a dia of 15 miles. There is the possibility that particle size black holes might be created and detected at CERN, but as of this date they have not been seen.
Planck unitsBlack hole radius
I've long heard of planck units for distance, time and mass, knowing they were 'natural' units, but hazy on the technical definition. Susskind says this system of units ginned up by Planck has the wonderful feature that three major constants of the universe all come out to be unity: c (speed of light), G (gravitational constant) and h (planck constant which shows up everywhere is quantum mechanics.) The starting point is unit of length (10^-35 m). Unit of time is the time it takes light to travel the planck length (10^-42) sec. This makes 'c' come out to be one. Susskind then says with the units of length and time so incredible small you might expect planck mass to be incredible small, but that is not the case. It's about the size of the smallest object you can see with the naked eye, a dust mote or 10 million bacteria (10^-8 kg or 10^19 Gev).planck length 10^-35 m
planck time 10^-43 sec (really 1/3rd of this value, since c = 3 x 10^8)
planck mass 10^-8 kg
R = 2GM/c^2 = (2G/c^2) x M
plugging in numbers to calculate the radius of a planck
mass mini-black hole (MKS system)
= 2 x 6.674×10^-11/ (3 x 10^8)^2 x 10^-8 kg
= 1.483 x 10^-27 x 10^-8
= 1.5 x 10^-35 m
check (10^-35 is the planck length)
Black hole temperature
Susskind clearly
relates the history of how Bekenstein figured out that black holes had
entropy, and that is was proportional to the area of the event horizon.
Hawking after first thinking this made no sense, changed his mind and ran
with it showing that black holes not only had entropy (which he calculated
exactly), but they had a temperature. Like any black body with a temperature
it radiates (photons), now called Hawking (or Bekenstein-Hawing) radiation,
which means it is continually radiating away its energy (mass), and lower
mass means a smaller black hole. A 'picture' for how Hawking radiation
comes about is to consider the virtual sea of planck time (virtual) particle
pairs that make up the vacuum right at the horizon. If one of the transient
pair finds itself inside the horizon, it's gone from this world, so it's
mate is converted into a real photon that is able to excape the black hole
gravity. The temperature of the hole comes out to be inversely proportional
to the mass of the hole, so at first it radiates slowly (very, very slowly
for an astronomically sized black hole), but as it gets smaller it gets
hotter and radiates more strongly until it eventually 'evaporates' away.
T = (h c^3)/(16 pi^2 G k) x (1/M)
where h = planck's constant, G = gravitational constant, k = boltsman
constant)
T in units of absolute temperature
plugging in numbers to calculate the temperature of a
planck mass mini-black hole (MKS system)
= (6.6 x 10^-34 x (3 x 10^8)^3)/(16 pi^2 x 6.674×10^-11 x 1.4
x 10^-23) x (1/10^-8)
= 0.24 x 10^-10/(1.47 x 10^3 x 10^-34) x 10^8
= 0.16 x 10^32
= 1.6 x 10^31 degrees absolute
check --- that's HOT
Susskind in his book says there is no real understanding of the details of hole evaporation, of what happens at energy levels like this. The energy of the protons and other particles that will be emitted is far, far higher than we have any experience with. I think the highest energy particles ever seen are a few cosmic rays with energy up around 10^19 ev (Wikipedia (ultra high energy cosmic ray)) only a few of which are seen per year. A 10^19 ev cosmic ray has about a million times more energy than big ring at CERN (14 Tev) can put into a particle!
Is a black hole really hot?The temperature calculated above for a minimum size black hole is easily extended to all black holes. The proportionality constant is unchanging, so it's a simple mass ratio problem. For example what would the temperature be of an earth mass size black hole, which if I remember right Susskind said was the size of a cranberry? The mass of the earth is 6 x 10^24 kg, so its ratio to the 10^-8 kg planck mass is 6 x 10^32. Scaling from above
I was thinking about what the 'temperature' of a black hole really means. Is a small black hole really hot inside? Who the hell knows, it's inside the event horizon. What the temperature of black hole really tells us is the energy level of the (thermal) radiation that we see coming from the black hole. A smaller the black hole must have an event horizon with higher curvature. My guess is higher space curvature is effective at smaller dimensions, where it is able to separate virtual higher energy particle pairs, capturing one and emitting the other. In other words I suspect black hole 'temperature' is really (just) a measure of the space curvature of the event horizon. This is the sense in which a small black hole is 'hot'.
T (earth mass black hole) = 1.6 x 10^31/6 x 10^32
= 30 x 10^-3 degree absolute
The sun has a mass 330,000 higher than earth, so
T (solar mass black hole) = 90 x 10^-9 degree absolute
Black hole entropy
Susskind relates
how Bekenstein came up with a thought argument to calculate what would
happen if a one 'bit' (of stuff, in reality a low energy photon) was thrown
into a black hole. A photon can have more than one bit of information (the
higher its energy the shorter its wavelength and the more localized it
is). His trick was to chose a very low energy photon whose wavelength is
the equal to the radius of the hole. He says this photon can't be localized
within the black hole which reduces its entropy to one bit. Susskind in
the book does the calculation showing what happens to the size of the hole
when one bit is thrown in. Of course, the hole gets larger because energy
has been gained, but its radius grows by an incredibly tiny amount.
This doesn't look interesting, but then Susskind says let's look at how
the area of the event horizon sphere (not its volume) has increased
and it is 10^-70 m^2. Whoo, this area is equal to the planck length (10^-35
m) squared.
Is this a coincidence? No says Susskind, Bekenstein made a fundamental breakthrough. The surface area of a black hole can be thought of as titled with planck area squares, and this is where the disorder is, where information is hidden, where the black hole entropy is. Entropy is a measure of disorder, a count of possible states of molecules or atoms allows the entropy of a body to be calculated. When Bekenstein first proposed that black holes had entropy, almost no one took it seriously (including Hawking) because the event horizon was thought to be a featureless, a perfect sphere ("black holes have no hair", said Wheeler). At that time there was no hidden information, nothing to count. These planck area squares as holders of information and entropy is the subject of Sussking's book 'Black Hole War', the entropy/information fight that Susskind is having (or had) with Hawking.
Black
holes merging captured by a gravity wave observatory (2/14/16)
The
big astronomical news this week was the detail capture by a gravity wave
observatory of the last 150 msec of two black holes spiraling around each
other and merging. This was a major event. A string of firsts involving
black holes, gravity waves, and engineering:
* First time two black holes have been seen merging.
* First time a solar binary composed of two black holes has ever been seen.
* First time gravity waves predicted by general relativity have been experimentally
detected.
* First time a gravity wave observatory has ever picked up an actual gravity
wave from an astronomical event!
* Confirmation of Einstein's general theory of relativity involving a super
high gravity event.
* Spectacular engineering achievement building an instrument that can measure
displacements one ten thousandth of a proton's dia.
* Excellent agreement of the signal to predictions from calculations and
modeling indicates black holes are very well understood.
In a surprise announcement this week a new window for astronomical observation opened. A gravity wave observatory in the US known as Ligo soon after it was upgraded in sensitivity and with lowered noise recorded the first ever capture of a gravity wave signal. The Ligo site says, "The field of gravitational wave astronomy is now a reality." This is high risk, big science paying off. The paper announcing the results has 1,000 authors! Some in the press oversold this as equivalent to the introduction of the telescope. Sure it's important and expectations are high, but a better comparison is the new windows provided by the first x-ray satellite, or infrared satellite or astronomical neutrino observatory.
Electromagnetic wave analogyLigo -- Laser Interferometer Gravitational-wave Observatory
There a interesting analog here with electromagnetic waves. No one had a clue that electromagnetic waves even existed in the 1800s until Maxwell found in his general equations of electromagnetism a wave equation, meaning electric and magnetic energy together could radiate as a wave. When Maxwell calculated the speed of these waves was always 3 x 10^8 m/sec, it had a spectacular realization because he knew (even in the 1860s) this was the speed of light, so while not 'proving' that light was a very high frequency electromagnetic wave, it very strongly (and correctly) suggested it. The equations supported electromagnetic waves at all frequencies, so a wide spectrum of waves might exist.Ok, the equations said electromagnetic waves could exist, but were they real? Was there any way to experimentally detect them? A few experimenters took up the challenge. Spark generators had been around a long time as they were one of the basic static electricity tools. Hertz designed two antennas and put them in the same room. In the transmitting side he interrupted a high current in the antenna with a spark gap. This produced a burst of high frequency waves from the antenna as the primary circuit rang. A receiving antenna picked up a fraction of the radiated energy and produced a tiny spark in the receiving circuit. By showing that the coupling between his antennas was different from induction that Faraday had earlier discovered, a purely s magnetic effect, Hertz was able to demonstrate that electromagnetic waves did indeed exist. This could be considered 'proof of principle' that wireless telegraph might be possible, and getting this far this took 20 years since Maxwell.
It took another 10 years or so before Marconi had the beginnings of useful device with his development of crude RF (radio frequency) detectors that could trigger a sounder. As he made engineering improvements, he was able to communicate over distances that got longer and longer. By 1901 he was able to span the Atlantic demonstrating that 'wireless telegraph' had the potential to be a practical way to communicate with ships at sea. By 1912 when the Titanic sank most new passengers ships had marconi radio rooms.
My crystal radioGravity waves
Even as a boy in the 1950s I had hands on experience with one of these simple RF detectors in a 'crystal radio' kit I built. To get the radio to work each time a spring loaded metal needle had to be moved around on the surface of a crystal while listening via headphones to find a spot where a station could be heard. The needle touching the crystal created a 'point contact' diode that rectified the RF carrier. With a little low pass filtering the audio that was used to amplitude modulated the carrier was detected. The needle, crystal and filter formed a simple, if wildly unreliable, detector of electromagnetic waves, which Maxwell had shown could exist 90 years before.
Just as with electromagnetic waves fifty years after Maxwell no one had given any thought to the existence of gravity waves until a wave equation popped out of the equations of general relativity (1915). (Actually it pops out of a linearized form of the equations.) Einstein went back and forth on whether he thought gravity waves might exist. For more than half a century after Einstein's equations nothing was done experimentally because calculations showed the displacements were so tiny as to be virtually undetectable. This changed only when the Ligo chief scientists began to think hard in the 70s about whether it might just be possible with a lot of clever engineering to build a really big laser interferometer that would be sensitive enough and quiet enough to have a chance of detecting displacements orders of magnitude smaller than the diameter of a proton.
NYT in an editorial about this discovery says at about the same time congress passed a bill requiring NSF grants be justified "in the national interest", and they note it is doubtful Ligo would have surived such political meddling. (Idiot republicans in action, crippling fundamental science projects.)More than ten years ago two identical detectors were build in Louisiana and Washington. Each detector has right angle pipes each 2.5 miles long run at a high vacuum. A laser beam is split and goes down each pipe bouncing back from a mirror at the end, and after many trips back and forth at the center the beams are recombined. If the length of either path changes, an interference pattern is seen.
Interferometers have long history as precision measurement devices. The classic michelson-morley experiment looking for the ether was the precision interferometer of its day. Michelson invented it and got it to work pretty well by careful choice of light sources, but it works better with coherent laser light. Ligo is the mother of all interferometers: super huge, super sensitive, and super quiet.The Ligo detectors ran on and off for about a decade as they were shaken out and repeatedly upgraded and not a single gravity signal was ever detected. This was not unexpected, because during this time the sensitivity was too low. During these years I read a book about Ligo, and at the time it was unclear if it was ever going to get quiet enough and sensitive enough to detect gravity waves. A lot new tricks were needed to further reduce the noise. You can't crank up the sensitivity if you don't get the noise down, the two go hand in hand if you want a useful device. Noise here means everything from motion of the mirrors to issues with the laser and detector and rejection of outside disturbances. I read that even quantum jitter of the mirrors was a noise source that had to be reduced.
What has been achieved in this detector is the ability to detect a dimensional change in a 2.5 mile tube that is four orders of magnitude smaller than nucleus of a hydrogen atom! This sound nuts, impossible, but it's been done, just look at the noise levels in the curves below. Achieving this has been a spectacular engineering and scientific achievement. The first event detected, the black hole merger, produced a displacement about three orders of magnitude smaller than a proton, but what counts is that it was x10 larger than the current limit of the instrument.
Building Ligo, a billion dollar investment, was an act of faith. And even without experimental proof other countries got on board building their own gravity wave detectors. There's even plans on the drawing board to build a gravity wave detector in space. It was probably the reputation of the three top scientists (Kip Thorne, Ronald Drever of Caltech and Rainer Weiss of MIT) who developed and pushed this project that got it funded. Weiss, who is now 83, gave MIT news an interview and said he was thinking about how to do this in the 60s for a class project as an experimental project to check Einstein's general theory of gravity. In the 70s he shared a hotel room with Thorne one night at a conference and the two of them stayed up late calculating and scoping out how to build a large scale detector that had a chance of detecting gravity waves that Einstein's equations predicted were out there in the universe.
Quick captureSignal captured
What happened with this first detection is very curious. According to the Economist magazine a major upgrade (taking years) just been completed in Sept 2015, going from 'Enhanced Ligo' to 'Advanced Ligo', but the Economist says it only increased the sensitivity by a factor of four, which doesn't seem like all that much to me. If a binary black hole merge like the one detected had occurred at half the distance (1/8th the detection sphere volume) it would have been four times stronger, so I'm puzzled that no event had ever been detected prior to this one. This event was captured almost immediately after the instrument began operating after the upgrade, in fact it was captured while the engineering shake out was still going on two day before the observing run was scheduled formally to begin. Such a quick capture makes everyone giddy that a lot more events are going to get picked up with the detector at its present sensitivity, and there are plans to increase the sensitivity further. It ran several months in late 2015, and the Economist says there are hints (rumours?) of other events in the data, but there has been no time to analyse them yet.
But there's much more. Prior to this observation much work had been done to calculate and model what sort of gravity signals were potentially detectable. Just as a motion of an electronic charge generates a 'ripple' in the electromagnetic field due to that charge that radiates out at the speed of light, the motion of a mass generates a 'ripple' in the distortion of space-time due to that mass that radiates out at the speed of light. Detectable signals were expected to come from orbiting neutron binaries at the very end of their life as they come very close together, orbiting in msec, moving at speeds that climb to a significant fraction of the speed of light, just before they finally touch and merger and ring down to form a larger neutron star.
The same thing was expected to happen if the orbiting binary was composed of a pair of solar size black holes, rather than neutron stars. In this case the signal would be even larger (?), because for a given mass the radius of a black holes is much smaller than a neutron star, so the rotation frequency, i.e. the acceleration, would go even higher before they merged. Until this event an orbiting pair of black holes had never been observed, while it was presumed they could exist, there was no data that they did.
Prior to the event calculations and modeling had been done for the type of signals that the detector could possibly detect. The excellent agreement between this calculated ringing and recorded ringing tells us a lot. It shows that black holes are well understood such that even a complex transient event like two black holes merging can be modeled accurately. I expect the masses of the two black holes, 29 and 36 solar masses, came from the computer model. The masses were adjusted until a good match was obtained.
The black holes that merged here are not the super jumbo black holes found in the center of galaxies. These are solar type black holes that either formed from the collapse of two very high mass stars that were in orbit around each other, or two black holes that got gravitationally attracted to each other. How the distance was obtained, 1.3 billion light-years, I don't know. None of the mainstream press articles explained this. This is really, really far away, about 1/9th of the distance to the edge of our observable universe. The articles said the calculated orbital velocity of the black holes as they merged was about half the speed of light (I check this below).
The calculated loss of energy to the gravity waves in this merge event is huge, about 5% of the initial mass of the two black holes is radiated away as gravity waves. Three solar masses gone into energy. And this happens in a fraction of a second! Compare this to the 0.7% loss of mass when stars burn hydrogen to form helium. The mainstream articles say that at its peak the energy output from the binary far exceeds (for a fraction of a second!) the energy output of all the observable stars in the universe. So this was a hugely 'bright' gravity event, but it occurred about a billion light-years away so the signal arriving on earth was very weak.
Eyeballing the curves below it looks like the last full cycle has a period of about 5 msec. This is 200 orbital revolutions per sec, or in motor units 12,000 RPM. At the end just before 'touching' a simple model (see below) shows the black holes were whipping around a 330 mile orbit in 5 msec, so they were indeed moving at a significant fraction of the speed of light (see below). Wow!
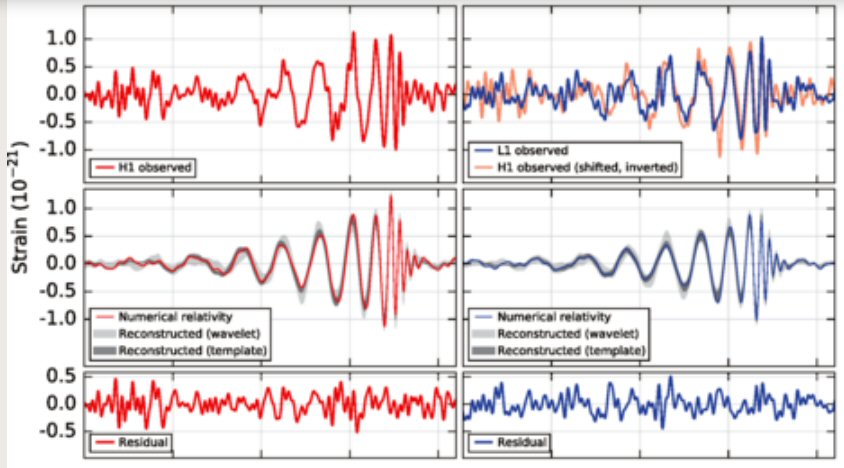
Ligo data, September 14, 2015 at 5:51 a.m EDT
Amplitude and frequency rise as the orbiting black
holes get closer and closer together.
Tick marks are 50 msec apart, so the whole observable
event lasted about 150 msec.
Last cycle period is roughly 5 msec (200 rotations/sec)
The signal came from the southern hemisphere since
it arrived at Washington 7 msec after Louisiana.
Working a few numbers
It's fun to
take a press announcement and understand it better by working a few numbers.
Just above is the formula for the radius of for a black hole. Let's see
how big a 30 solar mass black hole is. (MKS units)
R = 2GM/c^2 = (2G/c^2) x M
= 2 x 6.674×10^-11/ (3 x 10^8)^2 x [30 x 2 x10^30 kg]
= 1.483 x 10^-27 x 60 x 10^30
= 89 x 10^3 m
= 89 km (53 miles)
check: Economist mag gives the black hole size as 100 km
Let's do simple estimate of the orbital velocity when say the radius of the orbit just equals the radius of the holes. In other words if these were billard balls they would just be touching. Amazingly this quick and dirty little (classical) calculation using an orbital period I eyeballed off the curves comes out remarkably close to the Ligo value: (orbital) speed got to about half the speed of light. (I didn't fudge this, this was my first and only calculation!)
vel = 2 pi radius of orbit/period of orbit
= 2 pi x 89 x 10^3/5 x 10^-3
= 111 x 10^6
= 1.11 x 10^8 m/sec
check: 37% speed of light (3 x 10^8 m/sec)
------------------------------------------------------------------------------------------------------------------------------------------------------
Earth 1 AU distance
29.8 km/sec (av)
Saturn 9.57 AU distance
9.7 km/sec (av)
Note Saturn's distance (av) from the sun is (about) nine times that of earth, and Saturn moves (about) one third the speed of earth. We can guess from this that the (av) orbital speed of a planet (probably) vary inversely as the square root of its radius. The exact math (orbital speed of earth divided by sqrt of saturn/earth distance ratio) is 29.8 km/sec/sq rt (9.57) = 9.63 km/sec, very close to the rounded 9.7 km/sec of saturn. The orbital speed of all planets can be predicted this way. For example, Mercury at an (av) distance of 0.37 AU has an (av) orbital speed of 47.9 km/sec, pretty close to {29.8 km/sec/sqrt (0.37) = 49.0 km/sec}. Why is this?
The orbital velocity of a planet can be figured a couple of ways. From one point of view a planet in orbit is in continuous free fall toward the sun. If the gravitation force between the planet and sun were suddenly turned off, then the planet would fly off in a straight line. In a small (delta t) time the distance the planet falls toward the sun is just equal to the distance between the planet's 'fly away' tangent line and its curved orbit.
The same result can be calculated by viewing the inward (gravitational) and outward (centrifugal) forces on the planet as being in balance. Physicists take the point of view that centrifugal force is not a 'real' force, so this is not their favored approach, but it is physically intuitive and mathematically gives the same result. Each delta angle the change in the momentum vector (mv) is a quadrature vector of length mv x angle. Force is the time rate of change of momentum, so the centrifugal force formula is mvw.
gravitational force = centrifugal force
G x m planet x m sun/r^2 = m planet v w = m planet r
w^2 = m planet v^2/r
Solving for v (for earth)
v = G x m sun/r^2 x w
where
G = gravitational constant (6.67 x 10^-20 km^3/kg sec^2)
m sun = mass of sun (1.99 x 10^30 kg)
r = distance (av) from earth to sun (1.50 x 10^8 km)
w = orbital rotation (2 pi/T in rad/sec)
where
T = revolution time (1 yr = 3.15 x 10^7 sec)
substituting 2 pi/T for w
= k x m sun x T/r^2 x 2 pi
= 6.67 x 10^-20 x 1.99 x 10^30 x 3.15 x 10^7/2.25 x 10^16 x 6.28
= 2.96 x 10^17/10^16
= 29.6 km/sec (yes, it checks)
To show how the orbital velocity varies with radius we use the the relationship (v = r x w) to eliminate w from the centrifugal force equation. Solving for v (see below), we find that it is inversely proportional to sqrt(radius), confirming the relationship we guessed using planetary data. We also find that the orbital velocity is independent of the mass of the orbiting body (a good thing, otherwise spacewalks would be a no no!) and proportional to sqrt(sun's mass).
centrifugal force = gravitational force
m planet vw = G m planet x m sun/r^2
v x (v/r) = G m sun/r^2
v^2 = G m sun/r
v = sqrt{G m sun/r}
In the gravitational/centrifugal force balance equation planet mass appears on both sides and cancels out. Our moon and all man made satellites go around the sun at exactly the same (av) speed as earth.
Does
conservation of angular momentum apply?
My first thought
in figuring orbital velocities was to (somehow) use the conservation of
angular momentum. One of Kepler's empirically derived laws of planetary
motion (2nd law) is that planets sweep out equal areas in equal time.
This rule shows how the speed of a planet varies along its elliptical orbit.
We now know the reason a planet sweeps out 'equal areas in equal time' is due to the conservation of angular momentum. (The concept of angular momentum was unknown in Kepler's time.) A planet moving faster nearer the sun and slower when away is able to keep its angular momentum always constant. Angular momentum of a mass rotating about an axis in simple terms is just is the mass's linear momentum (mass x velocity) multiplied by the distance to the axis of rotation. In more general terms (angular momentum) = (radius) cross (linear momentum).
L = r x m v
where
L = angular momentum
r = radius
m = mass
v = (linear) velocity
Subtle trap?
Textbook's
commonly illustrate Kepler's 2nd law with a figure showing a planet in
an elliptical orbit with a cross hatched area swept out near the sun equal
to a cross hatched area swept out when far from the sun. The figure will
be labeled something like the 'law of planetary dynamics'. I think there
is a subtle trap here.
It's not much of a stretch, looking at the textbook's 'orbital dynamics' figure, and thinking of the conservation of angular momentum equation (rmv), to guess that a constant (radius x speed) rule applies to the speed ratios of different planets. This rule would predict that a planet's speed would vary inversely with its distance from the sun, but as we have seen above, this is not true. The orbital speed of a planet varies inversely as the square root of its distance from the sun. The orbital speed of Saturn, which is about nine times further out than earth, is about 1/3rd that of earth not 1/9th. Why does applying conservation of angular momentum (seem) to give the wrong answer?
Consider a comet with a strongly elliptical orbit that takes it from far out in the solar system down to 1 AU on its closest approach to the sun. A comet's dynamics are the same as for a planet. A comet, as in the textbook, is keeping its angular momentum constant as it travels its orbit. So when the comet is looping around the sun at the earth's distance (1 AU), is it going at the same speed as earth (29.8 km/sec)? No, it going faster! The reason for this is obvious upon reflection.
At the comet's minimum (1 AU) distance, it must (unlike the earth) have extra energy (in the form of kinetic energy) that will allow it to zoom away from the sun. Or from another point of view at 1 AU distance it is going faster than the 'free fall' speed toward the sun and that is why it slowly pulls away increasing its distance.
Bottom line --- Conservation of angular momentum can be used to find the speed of one body as it travels its orbit, but cannot be used to find the speed ratios of multiple bodies.Orbital period
Note, the calculation that orbital speed goes as 1/sqrt{r} depends includes an idealization. This is that the mass inside every planetary orbit is the same, or effectively that all the mass of the solar system is in the sun. In fact the sun has 99.86% of the mass of the solar system (says Wikipedia), and jupiter, which weighs (1/1,000) the sun has about 70% of the remaining 0.14% mass.Here's a table of planet 'years' using the scaling rule of radius to the 3/2 power. In this table the (av) radius is the average of max and min distances of the elliptical orbits. As you can see below, this simple scaling based on a circular orbit gives an excellent approximation. All data from Wikipedia.
| radius av (AU) | scaling by r^3/2 | actual (in earth years) | |
| mercury | 0.3871 | 0.2408 | 0.2408 |
| venus | 0.7233 | 0.6151 | 0.6152 |
| earth | 1.00 | 1.00 | 1.00 |
| mars | 1.5237 | 1.8807 | 1.8808 |
| jupiter | 5.2043 | 11.872 | 11.862 |
| saturn | 9.5821 | 29.661 | 29.657 |
| uranus | 19.229 | 84.323 | 84.323 |
| neptune | 30.104 | 165.17 | 165.17 |
| pluto | 39.482 | 248.08 | 248.09 |
No wonder it took man such a long time to figure out that planet orbits were not circular! The table above shows that simple, circular, orbit period calculations are very, very accurate (4 to 5 decimal places).
L2 lagrangian point
There's are
interesting exceptions to the 'rule' that orbital periods vary with the
distance from the sun. If you draw a line through the sun and earth there
are a two (nearby) points on that line where the orbit time is the same
as earth's. One is 1.5 mil km outside earth's orbit, far outside the moon's
orbit of (about) 420k km, and is called the L2 lagrangian point. The Wilkerson
Microwave Anisotropy Probe (WMAP), a major space probe that is mapping
the microwave background, is located there. The Wilkerson probe does not
orbit
earth. It just sits 1.5 mil km further out from the sun than earth and
travels with earth around the sun in one year.
Wikipedia has this neat figure showing gravity potentials of the sun-earth system..
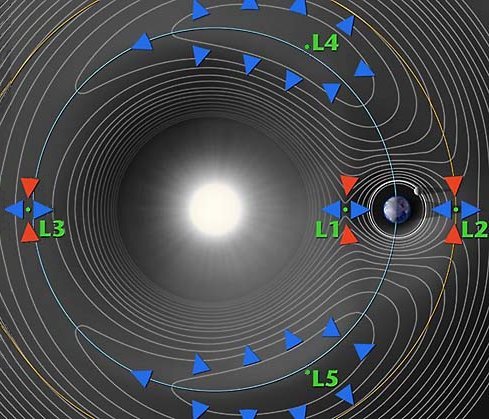
Lagrangian points (L1 to L5) mark positions where
the combined gravitational pull of sun and earth
provides precisely the centripetal force required
to rotate around the sun with earth
(Wikipedia -- Lagrangian point)
How does this work? The first thing I did (in my head) was some estimates. The (av) earth distance from sun is 149 mil km, so at 1.5 mil km L2's distance from the sun is almost exactly 1% more than earth's.
centripetal force
v^2/r
+1%
sun's gravity force
1/r^2
- 2%
The centripetal force equation shows a 1% higher inward pull (relative to the sun's gravity at the earth) is needed to speed up the velocity of objects at the L2 Lagrangian, but the sun gravity is 2% less there since the distance is 1% more. Hence the gravity of earth needs to make up the missing 3%. L2 is almost exactly 100 times closer to the earth than the sun, so (per unit of mass) the earth's gravity pull 100^2 =10,000 higher than the sun's. On the other hand the mass of the earth is much less than the sun, so the earth's gravity pull is reduced by the mass ratio. Therefore for objects at L2 to orbit with the earth, the following equation must be satisfied:
(m earth/m sun) x 10^4 =0.03
Above will be true if the mass of earth is 3 parts in a million the mass of the sun. I remembered that about 100 earth's fit across the diameter of the sun, so that makes the volume of the sun about one million times that of earth. So if earth's density is about x3 higher than the sun's, the equation is satisfied. When I checked the numbers (below), I found the sun's volume is a little more than 1 million times that of earth, but that is compensated for by the fact that the earth's (av) density is about four times higher than the sun's. Combining numbers the mass of the earth comes out to be almost exactly 3 parts in a million that of the sun as required. This explains why L2 is 1.5 mil km from earth.
Earth
5.5 x 10^3 kg/m^3
1.08 x 10^21 m^3 5.97 x 10^24
kg
Sun
1.4 x 10^3 kg/m^3
1.41 x 10^27 m^3 1.99 x 10^30
kg
The numbers are just about the same for the L1 Lagrangian. At L1 the inward pull on orbiting probes needs to be 1% less to slow them down, but the sun's inward pull is 2% higher. Hence earth's outward gravitation pull at L1 needs to be 3% of the sun's gravity, so L1's distance from earth is almost exactly the same as L2's (1.5 mil km). The SOHO solar observatory is at L1. In the future the Herschel and Webb telescopes are going to be put at L1 too.
The L1, L2
lagrangian points are unstable in the radial direction (blue arrows in
figure) and multiple objects need to be there, so L1, L2 probes are actually
put in (halo or lissajous) orbits around the lagrangian points.
---------------------------------------------------------------------------------------------------------------------------------------------------------
Newtonian
bending of starlight (5/12/09)
Einstein became
famous to the general public in 1919 when pictures taken by Eddington during
a solar eclipse (supposedly) verified Einstein's general relativity prediction
for the bending of starlight that passes near the rim of the sun. The Einstein's
prediction for the bending of light was (approx) 1.8 arc-sec vs 0.9 arc-sec
(Newton), or a factor of two between them. Data taken during solar eclipses
was never much better than +/- 1 arc-sec, so in 1919 the data scatter was
high and Eddington cherry picked the data he liked. Many year later radio
telescopes measurement were able to measure angular shifts of 0.01 arc-sec
or better for radio sources and Einstein's general relativity prediction
was verified to high precision.
Order
of magnitude calculation
I read the
Newtonian starlight bending calculation had been done as early as 1801,
by Soldner, who in 25 pages got about 1 arc-sec, when almost nothing was
known about the nature of light. This set me thinking, How do you calculate
starlight bending using Newton's laws? Here's a transcript of my scrap
paper order of magnitude calculation (without fudging).
The key starting point is that gravitational acceleration of an object is independent of its mass, because gravitation force is proportional to F = Gm1m2/r^2, but a = F/m1, so m1 cancels. It's questionable if this applies if light's mass is zero, but this is ignored. All relativity effects are ignored too.
* Time it takes
light to pass earth is about 8 thousand miles (earth dia)/186,000 miles/sec,
let's call it 0.04 sec
* Sun dia
is about x100 earth's dia, so it takes starlight about 4 sec to pass sun
* Gravitation
acceleration on earth's surface is about 10 m/sec^2
* Gravity
at radius of sun's visible edge is about x100 earth's (actually the right
value is x28),
so sun's gravity acceleration at rim is 1,000 m/sec^2
* Hor velocity
change of starlight (acc x dt) = 1,000 m/sec^2 x 4 sec = 4 x 10^3 m/sec
* Angular
deflection is just a velocity triangle. Angle is (4 x 10^3 m/sec)/c
=
(4 x 10^3 m/sec)/(3 x 10^8 m/sec), let's call it 10^-5 radian
* In arc-sec
10^-5 x (57 degrees x 3. 6 x 10^3 arc-sec/degree), let's call it
10^-5 x 200 x 10^3 = 10^-5 x 2 x 10^5 = 2 arc-sec
Son of a gun, this (2 arc-sec) is within about a factor of two of the right answer (0.9 arc-sec). (If I had remembered that the sun's gravity at its 'surface', something weeks earlier I had looked up, was x28, my bending estimate would still have been within a factor of two, just on the low side instead of the high side.)
Neutrinos
(I later dug
much deep into neutrinos than this short note, working for several months
to understand them and how they are detected. My long (48 page) essay on
neutrinos is here.)
Neutrinos are associated with the beta decay and the weak force. From the QED point of view neutrinos are associated with quarks changing type. A proton is two up quarks and a down quark, whereas a neutron is two down quarks and an up quark. So a (classic) beta decay of an atom, classically described as a neutron changing to a proton with emission of an electron, is down deep a down quark changing to up quark (via an intermediate W boson) with an electron and neutrino emitted as the W boson decays. The slow nature of beta decay, Feynman explains, is due to the high mass/energy of the W boson (about 80,000 mev).
Neutrinos were first speculated to exist in 1930 (by Pauli) to explain the missing energy in beta decay. Unlike alpha decay, where the emitted alpha particles all have about the same energy, in beta decay the emitted electrons were found to have a wide spectrum of energy. For most of the 20th century no one knew if neutrinos were truly massless, hence traveling at the speed of light, or had a tiny mass and traveled slightly slower.
Neutrinos are detected with big tanks placed in deep mines (to shield from cosmic ray products) filled with different liquids (chlorine, water, heavy water). The tanks are surrounded by photomultiplier tubes that detect a brief light flash (generated when a neutrino interacts with a nucleus). The detection rate at the Sudbury Canada Neutrino Detector is about 10 neutrinos an hour.
Most neutrinos hitting earth come from the nuclear reactions occurring in the sun. Neutrinos can also be detected (barely) from nearby supernovas. The most famous case is supernova 1987A in the large Magellanic cloud, where if my memory is correct, the Kamiokande detector in Japan detected a total of seven photons from that explosion.
A long standing mystery has been why neutrino detectors were only detecting 1/3 of the number of neutrinos predicted by detailed solar models. A recent PBS story about the new Sudbury Neutrino detector tickled me to investigate that the data from this neutrino detector may have finally resolved whether or not neutrinos have mass. This detector is sensitive to muon and tau neutrinos (muons and taus are basically high mass versions of electrons)
. Sudbury's heavy water data has confirmed (or helped to confirm) that "2/3 of the electron-type neutrinos produced by nuclear reactions in the core of the Sun are observed to change to muon- or tau-type neutrinos before reaching the Earth." To particle physicists this 'oscillation' of neutrinos between types as they travel from the sun to earth is proof that neutrinos have some mass. The present estimates of neutrino mass range from 0 .01 to 0.05 ev. For comparison the mass of the (light) electron is 511,000 ev (0.511 mev), so the neutrino is 10 to 50 million times lighter than the electron.
Here is a link to the Sudbury Neutrino Observatory:
http://www.sno.phy.queensu.ca/
How Hubble
telescope is pointed (3/2011)
I leaned from
a new PBS show how the Hubble telescope is pointed. This come from a Hubble
manager, so is probably right. He pointed out the telescope is moving at
17,000 mph all the time around earth, so to keep it pointed to arc-secs
in the sky is very demanding.
The technique uses special (he implied) super precise gyros, but their job is only to get the telescope near its target. The telescope is then held on its target field by a star tracking system using one (or more?) bright stars in the field of view. In every deep field image of Hubble I have ever seen there always seems to be a bunch of stars in our galaxy through which we have to look. These 'local' stars are generally obvious in the image showing up as bright over exposed points.
New
cosmic ray observatory (4/27/11)
As I write,
in two days a huge new observatory for cosmic rays, Alpha Magnetic Spectrometer-2,
is to be launched into space by the space shuttle for permanent installation
on the space station. This is a major observatory. Some are calling it
the Hubble telescope for cosmic rays. It's huge, about 15,000 lbs, built
and tested at CERN. It has super heavy magnet (2,600 lbs) that creates
a magnetic field of 1,250 gauss in the path of the instrument.
scan of Alpha Magnetic Spectrometer-2 from Scientif
American (May 2011)
Scientific American, where I first heard about it, says it almost didn't get launched. Pressure by scientists and congress got the shuttle program was extended just so it could be launched and brought to the space station. It will probably be the most important scientific instrument on the space station for its remaining years. A big advantage of putting it on the space station is that it need not carry all the support stuff a free standing satellite needs. The space station has big solar panels and can provide the 2,500 watts the observatory needs, plus it can keep it oriented and may be contributing ground link channels.
Cosmic rays
Cosmic rays are a variety
of high energy subatomic particles (and atomic nuclei?) that come in from
outer space, from who knows where, and rain onto the earth. The spectrum
of energies is wide with some far higher than what any particle accelerator
can generate extending to 20 Gev and higher. There might even be some anti-matter
or other exotic particles, say from dark matter mixed in. That's why this
is an important new instrument, so just what it is that coming in.
Some particles are positively charged, like protons, and some negatively charged, like electrons, and the purpose of the magnet is to detect the charge. A fundamental force law is F = q (v x B), or from another point of view a moving charge can be considered a current. If the magnetic field (B) is oriented across the path, then positive particles (+q) will bend one way and negative particles (-q) the other way, and the higher the charge the more the bending.
Wikipedia --- Cosmic raysMagnet
Here's what Wikipedia has to say about cosmic rays, and notice the numbers are a little inconsistent!90% protons m, +q
9% helium nuclei 4m, +2q
1% electrons m/2000, -q
1% other, heavier stuff ??
But the magnet in the observatory to be launched this week is not cryogenic, but a PM, in fact I read it is a magnet used in an early prototype that flew in the shuttle in 1998. It produces a magnetic field of only 1,250 gauss, or 1/8th that of the original. This means only 1/8th bending. It will however last for the life of the instrument, since it does not have a consumable like helium to run out. What happened? Well Wikipedia says at the last minute the superconducting magnet (which are always trouble) did not look reliable. It has "anomalous heating", in other words it was using helium at a faster rate than projected and for reasons not well understood, so it was removed and replaced with the older PM.
Project
I was surprised
to see that Ting of MIT originally proposed this observatory 1995 and since
has been the principal investigator. A prototype flew in the shuttle in
1998. Wikipedia lists the possible particles the detector might find:
anti-helium (nuclei) --- matter/anti-matter ratios are important
in cosmology
strangelets --- never seen, stable particles of up/down quarks with
strange quarks expected to
be very heavy with low charge, a totally new form of matter
neutralino (indirect evidence for) --- candidate dark matter particle
Galileo
Stoneham
HS talk (4/2/09)
Here are a
few slides I prepared for a high school talk on Galileo. The first slide,
where Galileo fits among early scientists, is an original by me. The resolution
slide is my scan from a book on the Hubble telescope. The heliocentric/geocentric
slide is from Wikipedia, and the images that show Venus as Galileo would
have seen it, I found on the web.
The Venus images showing a combination of size change and phase change is virtual proofthat Venus and Earth rotate around the sun with the venus inside earth. The size change is because (19 month cycle) the distance between earth and venus changes by about 3 1/2, as venus passed near earth and then is on opposite side of the sun from earth. There was the little problem of no (measurable) parallax to the stars, which it appeared that the heliocentric system should have.
Original figure, filename: galileo_figure.jpg (138kb,
4/2/09)
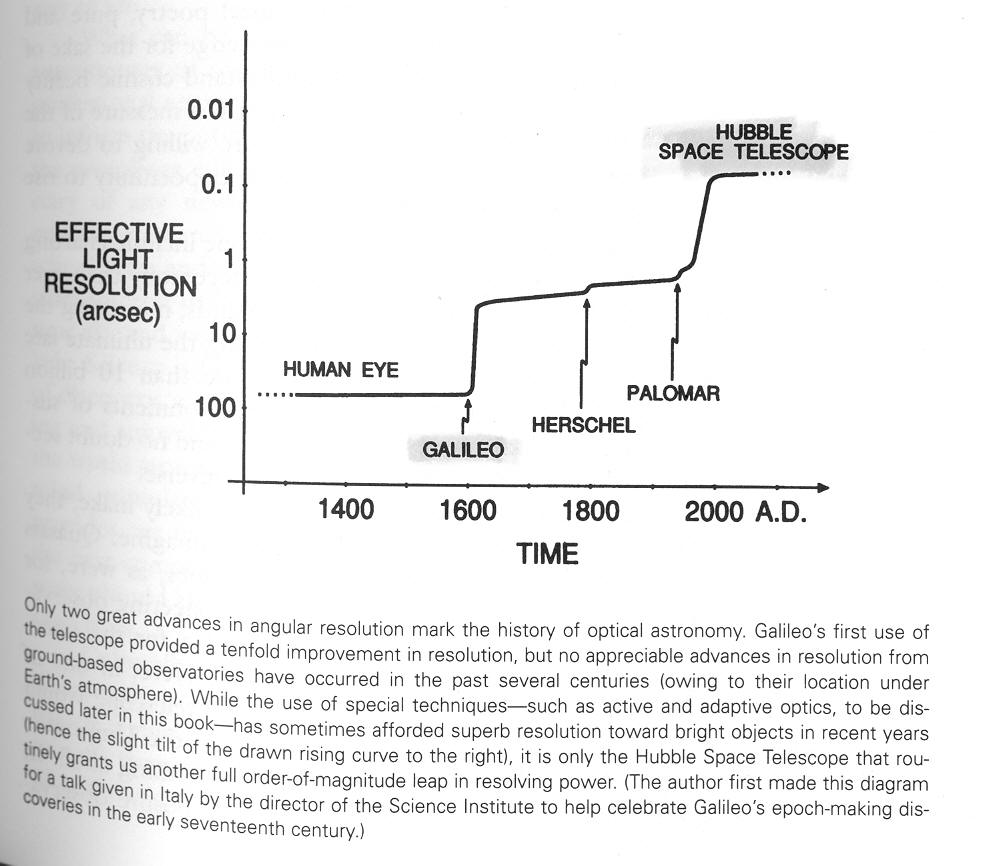
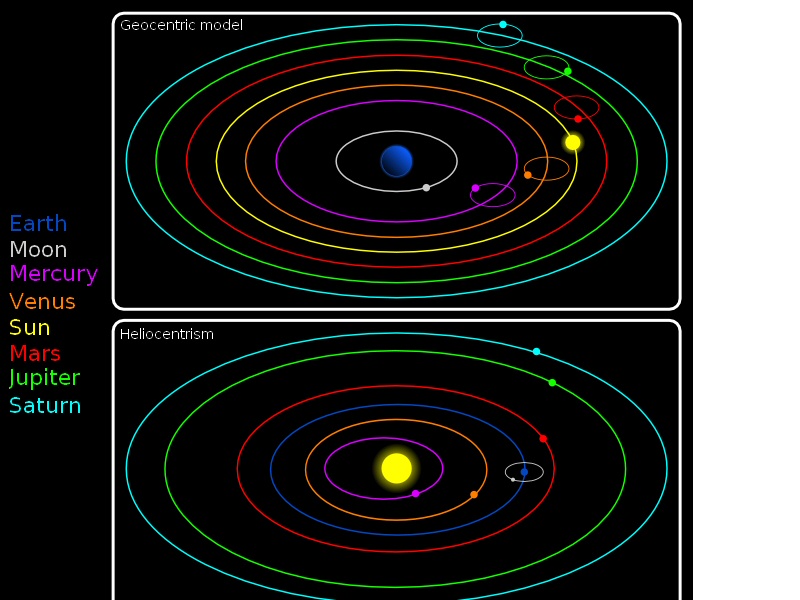
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Beautiful galaxy images




