My related essay on astromomy is here: Astronomy
Go to homepage
This essay is a few select topics from the huge subject of cosmology that I find interesting.
Beginning of the
universe
Expansion
of the universe -- Hubble's law
Did Hubble fudge his data?
Age
of universe
Newton's
universe
Olbers'
Paradox --- why is the sky dark at night?
Constants
of the universe -- a problem for cosmology
Constraints
for atoms and molecules to exist
Constraints
for carbon to be made
How
are free parameters set?
Universe with
no Weak Force
How
many protons and neutrons in the universe?
Probability
is zero
Anthropic principle
New
idea --- circumventing 'zero probability'
Cosmological
natural selection??
Big five of early
astronomy
Ptolemy
or (Claudius Ptolemaeus)
Nicholas
Copernicus
Heliocentric arguments pro
& con
View from earth
Epicycle
Johannes
Kepler
Galileo
Galilei
Tyco Brahe's
geoheliocentric model
A
third model of the world
Brahe
retains the geocentric star distance
Stars
have a noticeable diameter
Stars
need to be far, far away
Brahe
concludes heliocentric stars are unreasonably large
Either
earth rotates or stars move
Moving
earth contradicts common sense
Dark matter
Dark
matter 'halo'
Does
dark matter exist?
Type
Ia supernova --- Not so stable as thought?
Microwave
background temperature
Big bang electron
capture
Size
of the universe -- now and at decoupling
Why
cosmic microwave background (CMB) looks like a surface
Cosmic microwave
background maps
Higgs field
Scalar
field and mass
Has
earth been plowing through the higgs field for 4.7 billion years?
Cyclic universe theory
Dipole
in cosmic microwave radiation
How fast is
the earth moving?
Absolute
earth speed?
Where
did the earth get its organics?
Fifth gas
giant planet hypothesis
Liquid
water on satellites Enceladus and Europa
Beginning of
the universe
If you think
about it, there are only three general ways the universe could have
started --- It either started 0, 1 or ( 2 or more) times... Right?
There are no other possibilities. '0' starts is a universe that has been
the same forever, that has no known start, that has existed for an infinite
time. '1' start is, of course, the 'big bang' theory. '2 or more' starts
is a universe that has repeated beginning, a universe that is cyclic. In
both ancient times modern times all three possibilities have at one time
or another been considered a possibility.
The simplest case is no beginning; the universe is static, unchanging, time has no role. Not surprisingly this has long been a favorite model of the universe. It was the favorite model in Newton's time and up to the early 20th century. When it was found that the equations of Einstein's general theory of relativity did not allow for a static universe, Einstein changed the equations (by adding a term called the cosmological constant) because everyone 'knew' (including Einstein) that the universe was static not dynamic. A few years later in the 1920's with bigger telescopes and spectroscopes it was discovered that most 'nebulae' (now known to be other galaxies) had red shifted spectrums, which indicated they were moving away from us, and most importantly that the further away they were the faster they were receding. So the simple static universe was found to be not consistent with observation.
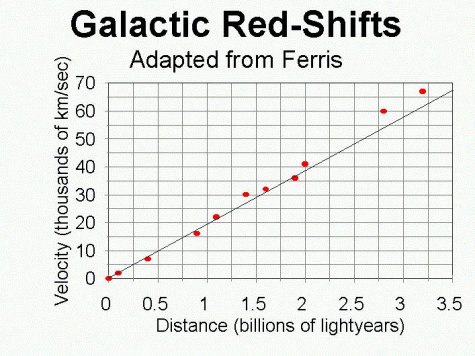
Expansion
of the universe -- Hubble's law
In the 1929
the astronomer Edwin Hubble using data from the new 100 inch Hale telescope
plotted (radial) velocity vs distance for a couple of dozen of the brightest
(nearby) "extra-galactic nebulae" (galaxies) for which he was able to obtain
distance estimates. He made his distance estimates, which he characterized
as "fairly reliable", by measuring the brightness of cepheid variable stars,
novae, and bright blue stars that he was able to resolve with the new Hale
telescope and assuming they were similar to those nearby (in our galaxy).
His data scattered around but did have a clear upward slope, so he drew a straight line through the data, saying in his 1929 paper, "The data in the table indicate a linear correlation between distances and velocities." It was a good guess and is now called Hubble's law. Over the years as data from galaxies further and further away became available the relationship between galaxy distance and their (radial outward) velocity has turned out to be (pretty close to) linear as you can see from the plot below (1980's plot). We now know that Hubble's 1929 distance estimates for his galaxies were far too low (by about a factor of 7), so Hubble's expansion rate came out far too high and his age of the universe far too low. Hubble's low age estimate for the universe was for a long time a problem because it was less than the estimated age of some stars and less than the estimated age of some rocks on earth.

Did Hubble
fudge his data?
I think there's
something very suspect about Hubble's data. Here's Hubble data from his
1931 paper, the second of his two papers on galaxy velocity vs distance.
(I found the figure below online, but verified that it has the same data
points that Simon Singh shows in his excellent book: Big Bang: Origin of
the Universe.)
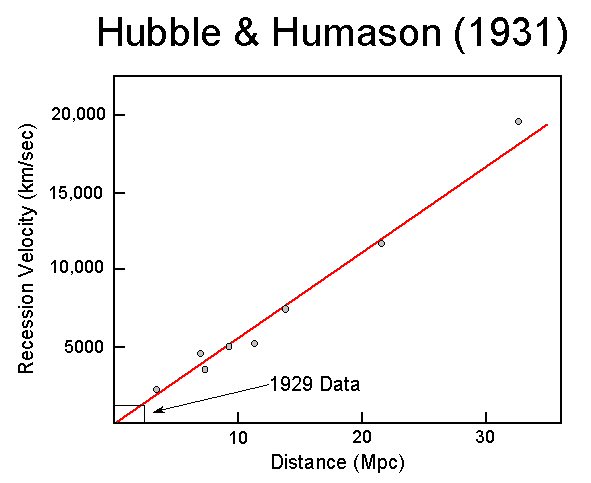
Data from Hubble's 1931 paper on relation between
galaxy velocity and distance.
(30 megaparsec is about 100 million light years, because
1 mpc = 3.26 light years)
If I put on my engineering hat, this data is very clean, every point is on or very close to the line. It's 100% convincing that the universe is expanding, and that is how it was received. Einstein was convinced. There's a famous photograph of Einstein looking through the Hale telescope eyepiece with Hubble looking on. Since Einstein's original equations for general relativity were consistent with an expanding universe, he dropped the cosmological constant fudge factor he had added to allow a stable universe.
Yet Hubble's distance measurements we now known to be way off. He has the distance for all the galaxies plotted here too close by about a factor of seven! His deepest data point that he estimates at a distance of 106 million light years (32.5 mpc) is really about 740 light years from us. How is it possible for his data to be so clean and so wrong? Clearly there must be systematic errors, but is that the whole story?
Singh points out that the famous astronomer, Jan Ort, argued in a (forgotten) paper published soon after Hubble's paper that Hubble's data didn't look right. These distances implied that nearly all the other galaxies were much smaller than the Milky Way.
Hubble was first famous for determining that andromeda was outside the milky way. Using the new 100 inch Hale telescope, which could resolve individual stars in andromeda, he found in it a few cepheid variables. Since they were about 100 times dimmer (for same period) than cepheids that Henrietta Swan Leavitt had measured in the small magellanic cloud, it meant, even without a calibration of the cepheid period-luminosity curve, that andromeda had to be x10 further away than the small magellanic cloud,. This was clearly placed andromeda outside the milky way, it was a separate galaxy.
It's tempting to think that calibration errors in the cepheid period-luminosity curve were one of the systematic errors in Hubble's data (above), but I don't think so. Hubble was an odd duck and in his book, which I read, he says very little about what he actually did to determine distance. Amazingly he didn't even include the 1931 plot above in the book! He included his (scatter plot) 1929 plot, and then just says 1931 data was basically consistent. I doubt, based on his andromeda photo, that he was able to resolve cepheids in very many (if any) other galaxies besides nearby andromeda. Hubble had determined andromeda was less than million light years away, so in the curve above, which goes out to over 100 million light years, it plays no part in determining the slope of the line, the hubble constant.
Hubble mentioned in his book that he also used the brightest stars (blue white supergiant stars). The working (first order) assumption here being that the largest brightest stars in any galaxy are likely to be about same, to have about the same intrinsic brightness. The technique would be to find as many as possible in a galaxy to try and average out any variations in intrinsic brightness. Now Hubble doesn't detail how he used them, but I think it likely he compared the luminosity of these bight stars in distant galaxies to the bright stars in the galaxy he could see most clearly, Andromeda. If this is what he did, it means any distance scaling errors to andromeda are reflected in all his galaxy distance measurement. If andromeda is too close by a factor of x, then all this other galaxy distances are going to be too close too by the same factor, meaning the slope of the line (Hubble constant) is too steep and Hubble time is too low.
It took 20 years or so and the new 200" Mount Palomar for the first systematic error to be found. At least for close galaxies like andromeda Hubble had used the [luminosity vs period] relationship found years earlier by Henrietta Swan Leavitt at Harvard to translate the period variations in cepheid variable stars that he actually measured to their intrinsic brightness. Walter Baade, who being a German and thus not recruited for war work during WWII, pretty much had the use of the 100 inch Hale telescope to himself during the war, and he discovered that like many types of stars cepheids came in two classes: population 1 and population 2.
Population 2 stars form after population 1 stars, so they include in their atomic make up higher levels of elements above helium, which astronomer call 'metals', that get added to star forming hydrogen clouds when large short lived population 1 stars explode. It turns out the Leavitt's cepheid period-luminosity relationship had been assembled using cepheids of one class in the small magellanic cloud, but Hubble in other galaxies was seeing only the very brightest cepheids, and these cepheids were in a different population. The intrinsic brightness difference for the two populations Baade found was about a factor of 4. Correcting for this error in 1952 (Wikipedia, Walter Baade) Baade moved all the galaxies out by about a factor of two, but that still left unexplained a distance error of x 3.5.
In a monograph from the Harvard observatory it said that Hubble in his more distant measurements had interpreted bright points on his plates as single stars, but that they were in reality star clusters. This could easily lead to big distance errors for his more distant galaxies. For example, if a galaxy cluster was say x9 brighter than a single bright star, Hubble would position the galaxy too close by a factor of 3 (= sqrt{9}).
Now we get to the heart of the matter: Did Hubble fudge his data? The cepheid class error would not effect the shape of the plot if all the galaxies were scaled to andromeda. It just rescales the plot, but leaves all the data points the same relative to the line. Ok, no fudging here.
But it seems to me the larger error due to mixing up star clusters with single stars does not lead to a simple scaling error. I would expect that the size and brightness of the clusters would be different in every galaxy. This would affect the shape of the curve. How is it then that Hubble's data falls so cleanly on a straight line? As my uncle used to say, I smell a rat. Was it just selective editing, perhaps even unconscious, that data points not on the line just got omitted?
My concluusion
Until I see
a more complete explanation, I suspect Hubble's 'too good to be true' 1931
curve (above) with nearly all the data points hugging the line was just
that, too good to be true. (At this point I have not done a detailed search,
so I have come across no one else who has concluded this. Most astronomers
when discussing Hubble's distance measurements just seem to mumble that
determining distance is hard and let it go at that.)
Age of universe
The slope
of the straight line above (galaxy velocity vs distance) is known as the
Hubble Constant. It is one of the most important numbers in cosmology,
because it tells us (approximately) the age of the universe. Notice the
the units of the slope are (delta y/delta x) = (distance/time)/distance
= 1/time. What this means is that the inverse of the Hubble constant (inverse
of the slope of the straight line above) is the age of the universe, the
time since the big bang. Technically it's called the Hubble age, because
it contains an assumption, which may or may not be true, that the expansion
rate of the universe has been constant (for a long time).
Reference
1 billion
light year = 9.47 x 10^24 m
seconds
in a year = 3.6x10^3 sec/hr x 2.4x10^1 hr/day x 3.6525x10^2 day/yr
= 3.16 x 10^7
Age of universe = 1/slope
slope of above = 19,500 km/ 1 billion light year (from
line above)
age of universe = 1 billion light year/ 1.95 x 10^7 m in seconds
= (9.47 x 10^24 m/1.95 x 10^7 m) x (1/3.16 x 10^7 sec/yr)
= 15.4 x 10^9 years
= 15.4 billion years (1980's value)
The current value of the Hubble constant/age of the universe is a little different from above. The data above comes from a book published by Timothy Ferris in 1989. A lot of work since then has been done (using the Hubble telescope and big earth telescopes) to get the best and tightest value possible for the Hubble constant/age of the universe. The currently accepted value is
age of the universe = 13.80 +/- 0.04 billion years (based on Planck and
WMAP microwave background satellites)
Hubble constant = 70 km/sec per Mpc (where Mpc 3.26 light years)
Newton's universe
Newton thought
(& stated clearly) the universe was not only unchanging in time, but
also infinite in extent. Newton had a good reason for believing the the
stars of the universe exended to infinity. Newton was the master of gravity,
and he understood that a universe with edges, meaning beyond some distance
there were no more stars, was a universe that would gradually collapse
together due to the force of gravity pulling all the stars inward. Even
though the pulling together might be very slow, it was going to happen
if the universe was infinitely old! So his solution was to have stars go
on forever in every direction. This produced a kind of stability. It was
also seemed simple, bypassing the classic philosophical problem of what
happens to a spear thrown at the edge of the world, and gave the universe
a nice symmetry in that it was infinite in both time and spacial extent.
But there were problems with having the stars extend to infinity. The first problem, which Newton (apparently) understood, is that the stability produced is not really very stable. The forces pulling on each star tend to null, but the null produced is what's called an unstable null. An example of an unstable null is a pencil balanced on its point. If it's perfectly vertical, then it continues to stand, but if it tilts just a hair, then gravity tends to tilts it more in the same direction, so it soon falls. In a system with a stable null if a part moves a little from its position, there is a restoring force that tends to push it back. Newton's only solution to this problem was to suggest that from time to time god might need to intervene (a little) to keep moving bodies moving and fixed bodies fixed!
The second problem with stars extending to infinity is it leads to a paraodox (Olbers' Paradox).
Olbers'
Paradox --- why is the sky dark at night?
Long after
Newton the astronomer Heinrich Olbers in the 1800's (supposedly)
asked the question -- Why is the sky dark at night? The (seemingly) obvious
answer, of course, is that at night the sun is on the other side of the
earth and only the stars are shining (let's ignore the moon for the purposes
of this discussion). But if you assume, as Newton did, that you live in
an infinitely old universe with an infinite number of stars extending in
all directions, then there is big problem. It should be very, very bright
at night.
Photographers know that the brightness of a surface (say a shirt) as recorded in a camera image does not depend on how close the shirt is to the camera. If you double the distance of the shirt from the camera, then the camera receives only 1/4 as much light from the shirt (light falls off as the square of distance). But the area of the shirt in the image is also reduced by 1/4, so two effects cancel, so any pixel on which the shirt image falls gets the same amount of light regardless of how far the shirt is from camera. (This explains why, in the old days before camera's had built-in light meters, a photographer could go right up to a surface with a light meter to take an exposure reading.)
Here is the problem with a universe infinite in extent --- If there are an infinite number of stars, no matter where you look in the night sky your view should fall on an the surface of a star. (Stars may look like points in the sky, but of course they are disk located far away.) It's like standing in a field in front of a forest. The tree trunks are spaced apart, but if you look far enough into the forest in any direction your view will eventually fall on a tree trunk. And because of the photographer argument it doesn't matter how far away the star is, the brightness you see will be like looking at the surface of our sun. If there is an infinite number of stars in a universe that is infinitely old, then the entire sky (night & day) should look like the surface of the sun! Hence the paradox.
The fact that it is dark at night, therefore, is an important piece of data. It tells us Newton was wrong, we do not live in an infinitely old universe populated with an infinite number of stars.
Constants
of the universe -- a problem for cosmology
The standard
model of particle physics since the 1970's has been used to calculate interactions
among all known elementary particles and forces of nature. This theory
has been well confirmed in that measured values are always found
to agree with calculated values, in some cases to matching to many decimal
places. However, in the theory all the masses of particles and values of
many of the forces in the model are 'dialed in by hand', meaning they can
be set at any value. In practice they are set by experiment. There are
19 or 20 of these so-called 'free parameters' in the standard model of
particle physics.
The free parameters pose a difficult problem for cosmological theories about how the universe started. The question is, why in our universe do they have the value they do? These numbers are all over the place, varying by huge ratios, (like 10^60 which is a very, very big number). Yet calculations show that small changes in some of these masses or forces, sometimes as small as 1% or so, prevent atoms from forming or stars from forming.
Constraints
for atoms and molecules to exist
Atoms are
made of protons and neutrons tightly packed in a nucleus with a diffuse
cloud of electrons orbiting outside. The mass of the neutron and proton
are very close (within 1%) and the electron is about 2,000 times lighter
than both. The force of the electromagnetic field holds the electrons to
the nucleus, but not so tightly that some can't get get loose to form chemical
bonds and create complex molecules. The nucleus is held together by the
'strong force' that must be stronger than the electromagnetic force, which
pushes protons apart. Another constraint is that the 'weak force' must
be just strong enough to overcome forces holding the nucleus together so
that some atoms are just a little unstable (radioactive -- atoms slowly
falling apart), while other atoms are stable. These three masses and three
forces are six separate parameters that in the current theory are (as far
as we know) independent. Ratios among all six of these parameters cannot
vary much before atoms and molecules as we know them won't exist. And this
is only six of the 19 to 20 free constants.
Constraints
for carbon to be made
Another classic
coincidence (??) is a particular resonance in carbon. Nuclear synthesis
in stars proceeds (mostly) by adding one proton at a time to the nucleus
(with some of the protons converting almost instantly to neutrons). This
is not too surprising since stars are mostly hydrogen. The problem is that
the proton addition process stalls after helium 4, because there is no
stable nucleus with atomic weight 5.
The table below
lists the longest lived isotopes of all atomic weights up to atomic weight
12 (stable carbon). Atomic weight 5 lifetimes of helium and lithium of
10^-24 sec are really short, so this justifies the statement that there
is no 'stable' atomic weight 5 nucleus.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lithium |
(5) |
10^-24 sec |
|
|
|
|
|
|
|
boron berryllium |
(8) (8) |
770 msec 7 x10^-17 sec |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
So while the masses and energies of atoms theoretically should allow stars to fuse atoms from element #1 (hydrogen) up to the element #26 (iron), for a long time no one could figure out how fusion could create element #6 (carbon) or any element higher. There are only two ways to build an element with six protons. One is three helium nuclei come together at the same time, but a triple collision is extremely unlikely. The other way is a collision between a nuclei with four protons (beryllium 8) colliding with a nuclei with two protons (helium 4). The problem was that calculations showed that beryllium 8 fell apart so fast (10^-16 sec) that almost no carbon (carbon 12) formed. No carbon, no life!
It turns out that what makes the fusion of carbon possible is that carbon has a resonance with an energy level that (almost) matches helium and beryllium. This resonance provides a longer time window in which these nuclei can fuse to form carbon, greatly increasing the likelihood of what is called the triple alpha process. Such a resonance had never been seen in carbon experimentally, but Fred Hoyle, who calculated it to be 7.65 MeV in the 1950's, argued it must exist, and when it was looked for it was found. In other words only because carbon has a resonance that matches beryllium + helium does the universe have lots of carbon and higher elements. Since this is very likely a narrow resonance (technically a high Q resonance), it puts further (likely tight) constraints on masses and forces in our universe if there is to be life.
Simon Singh has more detail (update 12/14/15)How are free parameters set?
Simon Singh's wonderful 2004 book [Big Bang, The Origin of the Universe] has a more detailed account of the carbon problem. Gamow and Alpher in the 50s had been hoping to show that all the elements were cooked up in the big bang, but they got stumped by what was termed the '5 nucleon crevasse'. In a sea of protons and neutrons the main path to nuclear synthesis was collisions that built up nuclei one nucleon at a time. This worked fine up to helium (4), where they had a big success correctly predicting the ratio of helium to hydrogen, but they got stuck at five nucleons. The five nucleon nuclei that are likely to form from helium 4 were helium 5 (neutron) and lithium 5 (proton), and both are super unstable with half lives around 10^-24 sec. Trying to jump the crevasse with two helium 4 colliding gave beryllium 8, which is not quite as unstable (10^-16 sec), but its rate of formation was probably also a lot lower, didn't work either. They were stuck.Lithium jumps 5 nucleon crevasseThe real hero of figuring out how most elements were created in stars was Fred Hoyle. He spent years calculating the temperature and pressure in the cores of different size and populations of stars and worked out the various reactions in the cores that could take carbon up to iron. Where he got stuck was he couldn't figure out a nuclear reaction that could make carbon from the helium and hydrogen in the core. There were two possibilities. Three helium 4 could collide at the simultaneously time to form carbon 12, but Singh says the probability of that was effectively nil. The other possibility was two helium 4 collide to form unstable beryllium 8 (10^-16 sec) and within its lifetime another helium 4 collides giving carbon 12. Calculations showed that this could lead to a slow rate of carbon formation, except there was problem.
Maybe this was discovered after Gamow's time, but during the big bang synthesis one element did jump the 5 nucleon crevasse: lithium. Some big bang references refer to lithium quantity as 'trace'. Most lithium (93%) is lithium 7 (3 protons, 4 neutrons) with the rest is lithium 6 (3 protons, 3 neutrons). Lithium 7 is helium combined with tritium and lithium 6 is helium combined with deuterium. Tritium is unstable, but that is irrelevant here as its half life is 12 years and big bang nuclear synthesis took all of 20 min or less. The (modern) calculated big bang synthesis ratio of lithium 7 to hydrogen = 10^-9 (by weight). There is no mention of any lithium 6 being created in the big bang, which I presume means the cross section of tritium was probably much, much higher than deuterium. [I remember reading Gamow's popular book on Big Bang synthesis while in HS around 1959, and to someone like me interest in science it was heady stuff.]Here's where the story takes an interesting twist. Singh says, "The combined mass of a helium nucleus and beryllium nucleus is very slightly greater than the mass of a carbon nucleus, so if they did fuse to form carbon then there would be the problem of getting rid of the excess mass. Normally nuclear reactions can dissipate any excess mass by converting it into energy [ E = mc^2], but the greater the mass difference, the longer the time required for the reaction to happen. And time is something the beryllium-8 nucleus does not have."
Here's a check using modern (isotopic) mass values from Wikipedia. The numbers below show the mass excess of [beryllium 8 + helium 4] over carbon 12 is about .0079 atomic unit or 0.79% the mass of a proton (938 Mev).
hydrogen 1 1.007825032 (938.272 Mev/c^2)
helium 4 4.002603254
beryllium 8 8.00530510
carbon 12 12.000000000 (by definition).007908 x 938 Mev = 7.42 Mev Check, pretty close to 7.65 Mev Hoyle calculated
Hoyle knew that excited states of nuclei were possible, the higher energy goes into the protons and neutrons rearranging, so it struck him that if the carbon 12 nucleus had an excited state with 7.65 Mev higher energy than normal, the second problem was solved and that a slow rate of carbon 12 formation in stars was possible. Singh says that at the time it was impossible to calculate the energy of excited nuclei states. Hoyle had arrived at his number by a logical argument extrapolating from known nuclear masses.
The story goes that Hoyle was on sabbatical at Cal Tech and wandered into the office of Willie Fowler, who Singh said was one of the world's best experimental physicists. Fowler initially said no way, carbon had been very well studied, and there was no hint of such a resonance. But Hoyle persisted arguing it would only take a few days work, and if it was found it would be one of the great discoveries of physics. Fowler found it in ten days, in 1983 winning the Nobel prize. Hoyle and Fowler together with E. Margaret Burbidge, Geoffrey Burbidge wrote all this up in one of the most famous physics papers ever published: Synthesis of the Elements in Stars" (1957).
However, the key guy in this story, the guy who did most of the work, who had the key idea, Fred Hoyle, was passed over for the Nobel prize in what Singh says was a huge injustice. Singh says this was probably because Hoyle had made enemies when he complained loudly about some earlier Nobel awards, like their passing over of Jocelyn Bell for the discovery of regular pulses from pulsars giving it instead to her thesis advisor Antony Hewish. (This was big news, I remember reading about it in Time magazine at the time.)
Another idea is that when our (or any) universe is formed the free parameters are set randomly. If all these parameters were determined randomly, and most need to be set within very narrow ranges, then, of course, it is extremely, extremely unlikely (and this is a gross understatement) that our universe would come to have the particle masses and force strengths that it does and which we believe are necessary for atoms, stars and ultimately life.
Smolin in the appendix of his book Life of the Cosmos, calculates the probability of free parameters being consistent for stars (black holes) and life, if randomly chosen, to be less than 1 part in 10^ 229. This is effectively zero because 10^ 229. is an absurdly large number. For reference let's calculate another large number and compare.
Universe
with no Weak Force
In an interesting
article in Scientific American (Jan 2010) two physicists (Jenkins and Perez)
have looked at varying several universal constant simultaneously to see
if other possible liveable universes can be created. The most interesting
case they present is the 'Weakless' universe. They turn off the weak force
and find that galaxies, stars, and planets can still form. That's right
a universe with only three fundamental forces instead of four! It asks
the question, what good is the weak force anyway?
What does the weak force do anyway? (I had to look this up to be sure). At the quark level the weak force is able to change the 'flavor' of quarks (up to down & down to up), which the electromagnetic and strong force can't do. So the weak force controls radioactive decay where protons turn into neutrons (& vice versa) and neutrinos plus electrons are spit out.
No stars?
It would seem this
would kill stars, because 'burning' hydrogen to into helium requires (net)
that two protons to convert to neutrons for every molecule of helium 4
formed. The dominant process in our sun is the proton-proton reaction,
which is four protons combining to make helium 4. It's a multistep, multi-branch
process, but starts with two protons joining to make deuterium, which of
course requires the weak effect because one of the protons converts to
a neutron. With no weak effect no deuterium can be formed in stars and
hence no burning of hydrogen to helium.
But there is a way out of the problem. In a weakless universe neutrons can't be made in fusion reactions in stars, they can be made in the big bang. The authors tweak a few parameters so the big bang yields both deuterium (proton + neutron) and hydrogen. Then weak stars can form by fusing the deuterium with the hydrogen to form helium 3. Actually the energy isn't too bad, about 25% of the dominant hydrogen burning process in the sun. In Wikipedia (Proton–proton chain reaction) the energy for each step of hydrogen burning in our sun is given:
proton + proton => deuterium
1.44 Mev
deuterium + proton => helium 3
5.49 Mev
(2) helium 3 => helium 4 + (2) protons
12.86 Mev (dominant pathway)
----------------------
19.79 Mev
check
E = [4 x proton mass - helium mass] (in Mev equivalents)
= 4 x 938.272 Mev - 4.002602 x 931.494 Mev
= 4 x 938.272 Mev - 4 x 932.100 Mev
= 24.69 Mev
OK ballpark (helium 3 pathway above is only 85%)
The article says computer simulations show this type of star could burn for 7 billion years with a power output of a few cent of our sun (no masses given). Large stars would not produce supernova explosions upon collapse, because it is the neutrinos that power the shock wave and no weak force means no neutrinos. Any planets would have no plate tectonics because there is no radioactive heating of the interior.
How
many protons and neutrons in the universe?
An easy was to estimate the number of protons in the universe is calculate
the # of protons and neutrons in the sun and multiply by the number of
stars in the universe. Our sun has 99%+ of the mass of the solar system.
The # of protons and neutrons in the sun is (very close to) the mass of
the sun divided by the mass of the proton. (below is an order of magnitude
calculation)
Reference
mass of sun
= 2 x 10^30 kg
mass of proton
= 1.6 x 10^-27 kg
Calculation of # of protons and neutrons in universe
# of protons + neutrons in sun = 2 x 10^30 kg/1.6 x 10^-27
kg=10^57
# of stars in an av galaxy = 10^11
# of galaxies
= 10^11
# of protons + neutrons in univserse = 10^57 x 10^11 x 10^11
= 10^79
The gas clouds in galaxies and the very thin gas in space (interstellar medium) increase the number a little, so maybe the number is 10^80 or so. But 10^80, every proton and neutron in the universe, is still like nothing compared to 10^229.
Probability is zero
A theory that
says the constants of the universe (technically , free parameters of the
standard model) are all independently set in a random manner (at the time
of the big bang) just doesn't make any sense. The likelihood of getting
a universe suitable for stars and life with randomly chosen parameters
is, for all practical purposes (a good engineering expression), zero.
Curiously, the same could be said of DNA and life yet somehow we have them. We know how the seemly impossible probability of life is has been achieved. A few say, of course, that this is an argument for an intelligent designer (aka God), but god is not necessary. What is impossible to do all at one time becomes doable if done in small (random) steps that can be in some way sequenced. This, of course, is how natural selection builds complex mechanism. It provides a way that small randomly occurring variations can accumulate and build complexity, all the biological complexity we see around us today.
Anthropic principle
One idea used to
explain (sort of) the value of free parameters is to point out that they
must,
at
least in our universe, have values consistent with life our universe has
life because we are here. This argument goes, maybe zillons and
zillions of universes have been created not friendly to life and a universe
with free parameters friendly to life, even though fantastically unlikely,
might have happened once, and no surprise, we find ourself in this statistically
unlikely universe precisely because it allowed for the development of atoms,
stars, and ultimately life.
The argument that, of course (we are here, aren't we!), we find ourself in a universe that supports life is called the anthropic principle. While it is embraced, sort of as a last resort, by many scientists, others consider it not a real scientific principle because it is not subject to falsification. Also, of course, as the probability of getting life friendly parameters (in one shot) approaches zero, this argument gets weaker and weaker.
New
idea --- circumventing 'zero probability'
Lee Smolin's
clever idea is maybe the complexity of the universe has developed in somewhat
the same way that the complexity of life has developed. Specifically that
some process has allowed a long accumulation of small random changes in
free parameters to walk around to find the rare sets of values suitable
for stars, black holes and life. His theory, briefly, is that black
holes give rise to new universes with parameters slightly different from
the parent universe. Therefore parameters (in most newly created
universes) will tend over time to walk to set of parameters that maximizes
he
number of black holes that form in a universe. Finally, that the conditions
favoring a large number of black holes, like galaxies, lots of carbon and
higher elements, long life stars, etc, are the same conditions needed
for life.
Cosmological
natural selection??
Less Smolin,
former Harvard professor and well respected theoretical physicist, in the
1990's proposed a new, dynamical theory to explain why the free parameters
in the standard model of particle physics have the values that are friendly
to life. He modeled his new theory after Darwin's theory of natural selection,
and he calls it Cosmological Natural Selection.
The core idea of Cosmological Natural Selection is that black holes create new universes. That the big bang of our and all universes come from the singularity (or near singularity) of a black hole in some other (parent) universe. A black hole collapse is the 'big bang' of a new universe. Pretty far out, no? When a black hole forms and the center squeezes into a singularity (maybe), this singularity creates a new universe! Smolin also assumes (postulates) that the free parameters of the newly created black hole universe are somewhat close to the free parameter of the universe that spawned the black hoe. In effect the black hole is the parent of the new universe and passes on its 'genes' (really , free parameters) to its offspring with some small variation.
The analogy with Darwin's natural selection is obvious. In (real) real natural selection the process that leads to the accumulation of small random variations (of life parameters) into a more useful set of parameters is more offspring surviving to reproduce. Species derived from those with the most offspring in the past are the only species we see around us today, all others have died out. In Cosmological Natural Selection the 'offspring' are black holes. So universes that are most likely to have survived and to exist today are those that have free parameters that maximize the probability of forming black holes.
This may seem like wild speculation, but Smolin makes many good arguments in his book (Life of the Cosmos, by Lee Smolin, 1996) that this, unlike the anthropic principle, is a real scientific theory subject to falsification. And furthermore that as far as is known it it is consist with the facts, that free parameters in our universe do seem to be at or near the values that maximize the probability of black holes.
Big five
of early astronomy
The big five
of early (western) astronomy are Ptolemy (150 AD), Copernicus (1543), Kepler
(1609), Galileo (1610), and Newton (1687). All of them wrote (at
least one) famous book. Ptolemy, Copernicus, and Kepler developed models
of planetary movement and using detailed mathematical analysis showed that
their models explained all observations of the heavens.
Ptolemy's model had the fixed earth in the center and all other bodies (including the sun and moon) rotating around earth in complex circle-upon-circle (epicycle) orbits. Copernicus's model placed the sun in the center and had all other bodies (except the moon) rotating around the sun in complex circle-upon-circle orbits. Kepler 'fixed' Copernicus's sun centered model by figuring out the correct shape of the orbits (ellipses) and a precise rule for how the speed of the planet varied along its orbit.
Galileo principal contributions to astronomy were experimental. He developed the first telescope (refracting telescope) and used it to make many astronomical discoveries that he quickly publicized. Newton was both theoretician and experimentalist and made several major contributions to astronomy. Newton worked out a theory of gravity and a complete theory of mechanics that allowed Kepler's orbits and speed of travel on the orbits to be derived mathematically. Newton invented new mathematics (calculus), far more powerful than the geometry used earlier, to describe the motion of the heavenly bodies. Newton's contribution as an experimentist was the development of new type of telescope, the reflecting telescope. All big telescopes today are (Newtonian) reflecting telescopes.
Ptolemy
or (Claudius Ptolemaeus)
Quick view:
Wrote the definitive book (Almagest) about 150 AD documenting mathematically
how the heavens rotate about a fixed earth. The orbits of the sun, moon,
and planets were a combination circular deferents plus epicyles (and various
other tweaks).
His geocentric model, while very complex, did a good job of explaining known measurements of the heavens, which had been taken for hundreds of years, and, of course, it fit with the common sense view that the earth is motionless.
Nicholas Copernicus
Quick view:
In 1543 Copernicus proposed a heliocentric world view where the earth and
all planets went around the sun.
Copernicus was both a mathematician, which in those days meant geometer, and astronomer. He took Ptolomy's data and combined it with more recent data, some of which he himself had taken, and worked out the most accurate formula and tables yet devised to explain and predict positions of the moon and planets. All these calculations are included and make up most of his famous book On the Revolutions of the Celestial Spheres.
de Revolutions in its detailed calculations was immensely complicated, and the book is also famously turdid in its prose (and considered by some almost impossible to read). The complications are due almost entirely to the fact that Copernicus orbits were circular with superimposed epicycles, similar to, but not quite the same as, Ptolomy's.
Heliocentric
arguments pro & con
It appears
that Copernicus did not really emphasize (hammer home) the fact that a
sun centered universe provided a natural explanation for several
otherwise hard to explain motions. (Was it was deliberate to sneak the
new theory in under the radar of the church and its censors, or was he
just a bad writer? Who knows?)
--- Retrograde motions of the planets (seen against the sphere of fixed stars) now makes sense. The orbit times of all the planets at the time were known quite well. The retrogrades of planets can be seen (by simple sketches) to be caused by the fact that the earth rotation rate about the sun is different from all the planets. In the case of the outer planets retrograde motion occurs when the earth overtakes and passes them. In the case of the inner planets it's how we see them as they overtake and pass us.

Composite showing three years of Saturn in the night
sky, showing three retrogrades
--- Why Mercury and Venus always stay close to the sun is explained. In Ptolomy's system it had to be assumed (for no good reason that I am aware of) that the inner planets (Mercury and Venus) traveled around the earth on deferent circles that rotated at the same speed (and in phase with!) the sun. Their epicycles explained why Mercury and Venus moved back and forth relative to the sun. But when you sketch out Copernicus's heliocentric orbits, it's immediately obvious why Mercury is always real close to the sun and Venus somewhat less close. (figure)
These two points alone make a strong case (at least in the modern view) that the heliocentric model was more likely than not to be right compared with the geocentric model. Motions of the planets just made more sense. There was, however, a (substantial) astronomical argument to be made that the heliocentric system was not compatible with the data. This is, of course, in addition to the arguments from the Bible, and the common sense view that the earth feels stationary, that supported Ptolomy's fixed earth model.
--- The astronomical argument is that if the earth is moving about the sun, and the sphere of stars are centered on the sun, then the angle (parallax) to stars overhead should vary a little (to and fro) every six months. But in fact stellar parallax (at the time) appeared to be zero consistent with a geocentric model.
We now know the explanation is that the stars are so far away that the parallax is tiny. It is in fact virtually zero for most stars and less than an arc-sec for even the closest stars. At the time there was the idea that stars might be distant sun's, so it was not unreasonable to view stars as pretty far away. However, no one had any (quantitative) idea what the distance to the stars might be, even though at the time the size of the solar system (in relation to the size of the earth) was (approx) known. In fact it took about three hundred years after Copernicus before astronomers were able to measure the parallax to a few stars, thus providing the first hard data on the distance to any star!
View from earth
Ptolomy and
Copernicus did yeomen work. Think of the complications they faced trying
to come up with accurate positions of all the objects in the heavens from
a tilted, precessing, spinning, rotating, loop-de-loop wobbling earth.
Just look at how Saturn in the figure above moves relative to the stars.
(Try and model that, and that's just the tip of the iceberg!)
The view of the heavens from earth, when looked at closely over time, is immensely complicated. The earth is not only spinning on its axis, but its axis wobbles (precesses), a fact which was known, and had to be accounted for, by the ancients. The earth (and all the planets too) goes around the sun in a path that is close to a circle, but is not really a circle, it's an ellipse (approximately). That planetary orbits are ellipses was figured out a couple of generations after Copernicus by Kepler in the 1600's. (Wikipedia reports that an Indian astronomer had figured out planetary orbits were ellipses in 499, about 1,100 years earlier.)
An ellipse is a generalized circle, sort of a circle with two centers. In a circle the distance to the (one) center is constant (radius). In an ellipse the combined (summed) distance to the two centers (foci) is constant. (The sun sits at one of the two foci of each planetary orbit.)
Another serious complication (to modeling the heavens from earth) is that the earth travels on its orbital path at varying speeds, slightly faster when closer to the sun and slightly slower when father away. And, of course, all the planets do the same thing. We now know the variation in speed is due to the conservation of angular momentum. The product of distance and speed is a constant. The equation for angular momentum on a circular path is (L = r x p), where the angular momentum vector (L) equals radius vector (r) crossed with the linear momentum vector (p = mv).
A still further complication is that the earth travels on its elliptical path with a small superimposed loop-de-loop motion, with (about) 12 loops per rotation around the sun. The cause of this looping is the earth's moon, specifically the monthly rotation of the earth and moon around their common center of mass. It is the center of mass of the earth/moon system that travels in an ellipse around the sun. I am not sure if Ptolomy and Copernicus had any grasp of this small effect. In their times there was, of course, no theory of gravity to predict (and explain) this effect.
Epicycle
It's easy
to dismiss epicycles as artifacts of the past and just plain wrong. But
are they?
I just realized that the earth's path around the sun does in fact include a real epicycle. If you view the earth (say from above) relative to an ideal ellipse (ignore the small distorting effects on the ellipse from other planets, or the slight wobble of the sun itself), then the earth is moving on an epicycle whose center (center of mass of the earth/moon system) moves on its deferent, which in this case is not circular but is a Keplerian ellipse.
Johannes Kepler
Quick view: Kepler is the last of the big three mathematical modelers
of early astronomy (Ptolomy, Copernicus, Kepler). Kepler wrote a
book in 1609 (Astronomia nova) that argued that the paths the planets
(& earth) take around the sun are ellipses (not epicycles on deferent
circles). And he figured out mathematically, without a theory of
gravity, how the speed of plants vary along the elliptical path.
These two changes drastically simplified the mathematics of the heliocentric
model and conceptually strengthened it.
Galileo Galilei
Quick view:
Galileo greatly strengthened the case for a heliocentric system with his
observations of the heavens using one of the first telescopes. He quickly
wrote up his telescope observations in a 1610 book called The Starry
Messenger. In it he reported:
-- There were tons more stars than could be seen with the naked eye
(& the sky through the telescope appeared to have depth)
-- Four moons could be seen orbiting Jupiter
(This rebutted an objection that dogged the Coperician theory. According
to Copernicus the sun powered
all six planets to rotate around it. But if the earth moved around the
sun, it meant it had to be dragging
the moon along with it. How likely was this? The orbiting Jupiter satellites
showed it was possible.)
-- Our moon appears to have valleys and mountains
(it looks a lot like earth)
Three years later he wrote another book on his solar observations (Letters on Sunspots). In it he notes it is obvious that the sun has spots, so it is not perfect (as had long been argued). He tracked how the spots moved over time, finding they moved in arcs across the circular disk, and from this he concluded it was more likely than not that the sun was titled on its axis and was rotating.
Tyco
Brahe's geoheliocentric model (12/13)
A recent article
in Scientific American about Brahe and his model of the world has information
I had never heard before. The key reason say the authors that Brahe was
unable to accept heliocentric model of Copernicus was its requirement that
stars be very far away, which when combined with his measurements of stars'
angular size, meant they had to be much, much larger than the sun! He thought
this improbable as stars seemed likely to be distant suns.
The 'star size' problem of the Copernican heliocentric universe was the "most devastating argument" against it say the authors.
A third model
of the world
In Galileo's
time there weren't just two models of the world, there were three. Tycho
Brahe, the world's greatest observational astronomer up that time, came
up with the 3rd model: geoheliocentric model, which is sort of a compromise
between the traditional geocentric model and Copernicus' heliocentric model.
Most references give Brahe's model short shrift, barely mentioning it.
So it was with interest I read an article in Scientific American (Jan 2014)
that makes some interesting points about "Brahe's new cosmology", one point
in particular I had never heard before and is very interesting.
Brahe's geoheliocentric model is below (left). Some aspects of it are the same as in the traditional geocentric model (right). The earth (green) is at the center (unmoving as before) and orbiting around the earth are the moon, sun and stars. (Ignore the orbital spacing differences in the figures, which for some weird reason are drawn differently.) However, Brahe's model differs from the geocentric model in that the known five planets go around the sun, which in turn orbits the earth. Note Brahe's figure shows the orbits of mercury and venus not encircling the earth, while the orbits of mars (red), jupiter (yel) and saturn (orange) do encircle earth. The result is that the relationship between the earth, sun, and all the planets is the same in Brahe's model as in the Copernican model (see below). It's almost like Brahe just took a sketch of Copernicus' heliocentric model and just stuck a pin through the earth pining it to the table, saying this is the unmoving center not the sun.
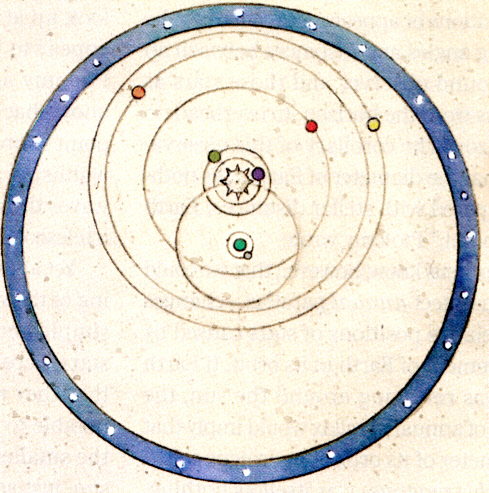 .
. 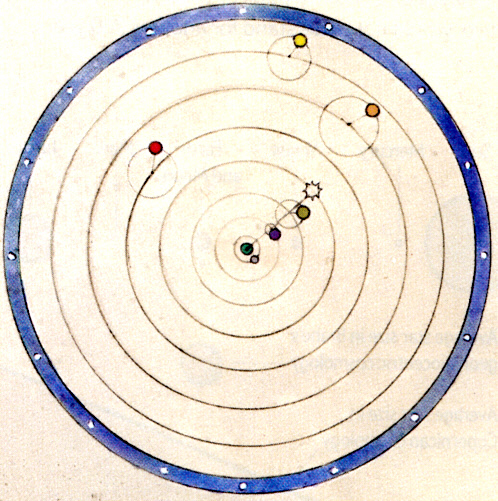
Brahe's geoheliocentric model
geocentric model (traditional)
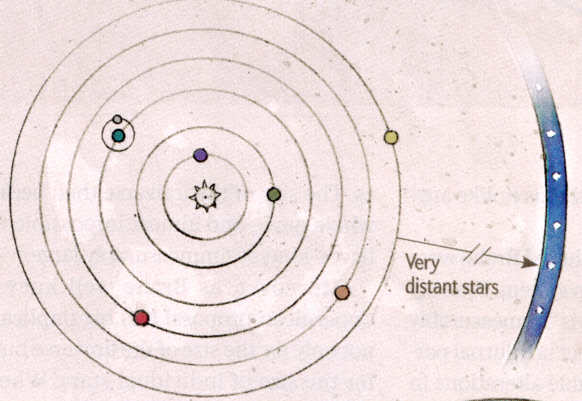
Copernicus heliocentric model
(scans from Scientific American, Jan 2014)
Brahe
retains the geocentric star distance
However there
is one relationship difference between Brahe's geoheliocentric model and
Copernicus's heliocentric model, and this is how the stars are positioned
relative to the earth. Copernicus has the sphere of stars centered on the
sun,
while Brahe has the sphere of stars centered on the earth. To an
observational astronomer like Brahe this makes a huge difference, because
it allows the stars to be much closer to the earth, and this in turn solves
a nasty problem that Brahe recognized in the heliocentric model.
Stars
have a noticeable diameter
The problem Brahe
saw in the heliocentric model involved the angular size of the stars. Brahe
as the world's greatest observational astronomer could see that stars on
close inspection did not look like tiny pin points in the sky, but had
a noticeable diameter, a diameter that he had measured. This angular star
data
meant
Brahe had some knowledge of a relationship between the (true) size of stars
and their distance. For example, if a star diameter appeared to be 1/1,000
(just my guess) the dia of the sun, and if an assumption is made that its
true size is close to our sun, then it must be located about 1,000 times
further away from earth than the sun.
Wave nature of lightStars need to be far, far away
Now it turns out that stars really are just infinitesimal small points of light in the sky. The small diameter that stars appear to have is really an artifact of the wave nature of light, due to how it spreads out when going through a small opening or lens including the lens of the eye. But the theory of the wave nature of light was far in the future, so Brahe knew none of this.
Brahe
concludes heliocentric stars are unreasonably large
Brahe understood
that if Copernicus' model required stars to be much further away than in
the geocentric model then that meant they must be much larger to retain
at the same angular size. If in the heliocentric model stars are say 100
to 1,000 times further away than in the geocentric model, then that means
their real size must be 100 to 1,000 times larger for them to have the
same angular size. When Brahe worked out the implied true star size in
a heliocentric system, he found star size came out to be far, far greater
than the size of the sun. This did not just seem reasonable to him. He
guessed that stars were most likely other suns at a distance, and this
was consistent with the geocentric model. Hence Brahe's model solved the
heliocentric 'star size' problem by putting the star sphere back where
it had always been, a sphere centered on the earth. Yet by having all the
planets, even the earth from one point of view, going around the sun, he
retained much of the simplicity and elegance of the heliocentric system.
Either earth rotates or stars moveMoving earth contradicts common sense
With this relocation of the stars he solves the star size problem, and with an unmoving earth Brahe's model agrees with the common sense notion that the earth does not move. But the tradeoff is that he has to reintroduce the need for the star sphere to rotate around the earth once a day. This is a nasty tradeoff to which at the time there was no good solution. It's obvious to anyone on earth that at night the whole star sphere is rotating overhead. In just minutes rotation can be sensed, and over the course of a night all the stars together will rotate through a substantial portion of the sky. So either the stars have to move or the earth is rotating. There is no other possibility. Of course star movement at the time may not have been seen as a big problem. It had always been this way, and the ancients had finessed the issue by saying stars were made of aerial stuff and that the nature of this material was to move.
Dark matter
Dark matter
has been postulated to explain a curious fact. When the rotational
speed of stars around the center of a (spiral) galaxy are measured (using
the doppler shift in their absorption lines) across the radius of a galaxy,
the resulting curve for most galaxies is pretty flat. In other words. the
stars on the edge of the galaxy are moving as fast as the stars near the
center! This was (and is) a real puzzle. If the mass of a galaxy is where
we see the stars, then star on the edge rotate more slowly than stars near
the center. In orbit the gravity force must be balanced by the centrifugal
force outward, so lower gravity means lowers speeds. Similar unexplained
high speeds are also seen in gravitationally bound cluster of galaxies.
In the solar system where nearly all the mass is in the center (in the sun) the further out a planet is the slower it goes. The formula, which I derive in the astromony essay, is
v = sqrt{G m sun/r}
Saturn is about x10 times (x9.6) further from the sun than the earth. It's velocity is about 1/sqrt{10} that of earth (10km/sec for Saturn vs 30 km/sec for earth) and the circumferance of its orbit is about x10 earth, so Saturn's rotation time is (about) x30 longer than earths. Consider earth satellites: Low orbit satellites go around in about 90 minutes, high orbit satellites in 24 hours, and the moon takes a month.
Dark matter is a misnomer
'Dark matter'
is poorly named. Dark matter interacts via gravity, but it doesn't interact
at all with light (photons). Hence it is not dark, it is invisible (a
point Lisa Randall of Harvard makes in her new book).
Dark matter 'halo'
The rotational
speed of a star in a galaxy (about the galaxy center) depends only
(if the mass is fairly uniformly distributed) on the mass enclosed within
the
orbit. Since in a spiral galaxy most of the visible mass of the galaxy
is in the center bulge, a plot of star speed vs radius was expected to
rise from zero and peak (roughly) near the edge of the bulge, and then
to roll off (approx) as 1/(square root of r), specifically sqrt{G
galaxy mass/r}, as shown in yellow below.
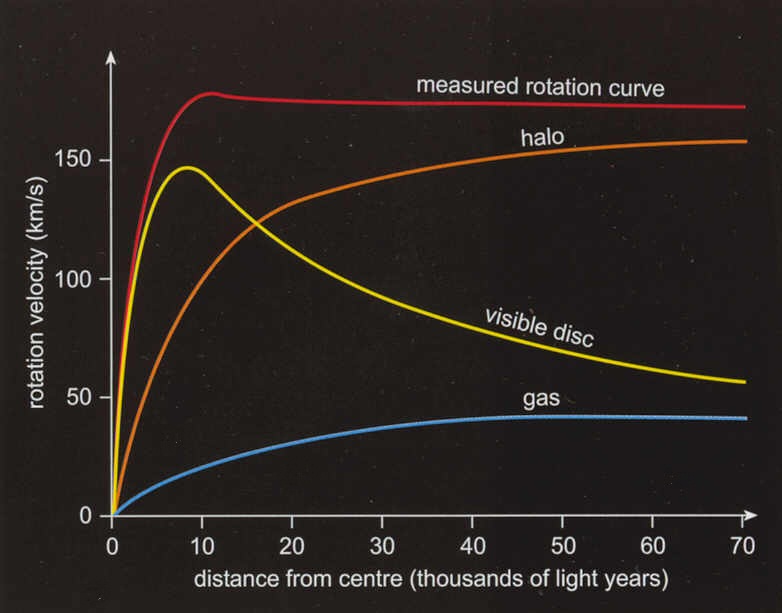
scan from 2007 book "Dark Side of the Universe: Dark
Matter, Dark Energy, and the Fate of the Cosmos", by Iain Nicolson
The formula for rotational velocity of any star in a galaxy is
v = sqrt{G mass inside orbit/r}
so to get a flat rotation curve (v independent of r) requires that 'mass inside orbit' go up as r. Or said another way the mass enclosed in a sphere at radius r must increase linearly with r, which implies a mass density that falls off as 1/r^2. The reason this works is that the volume of a sphere go up as r^3. I found this simple explanation (and the figure above) in a new astronomy book by Nicolson that I am now reading .
Why didn't I understand this earlier? I think it's because the distribution of dark matter is almost always stated this way:
"A halo of dark matter encloses the galaxy"
This is very misleading, if not just plain wrong. A halo goes around the outside of your head. If the dark matter is distributed only outside the visible disk, which is how I had interpreted it, then it has no influence on the stars' rotation, because rotation speeds depend only on the mass inside orbits.
The dark matter thesis requires that the visible galactic disk be embedded in dark matter that extends in (at least) as far as the galactic bulge and has a mass density that falls off as 1/r^2. Since radio wave studies and other techniques show the flat rotation characteristic can extend far beyond the visible mass, the dark matter material must extend far beyond the galactic disk. The 'Dark Side of the Universe' book says the milky way's galactic dark matter 'halo' is thought to extend out to 500,000 ly, which is about x10 the radius of the visible disk.
In fact, Nicolson says the "simplest models" of dark matter WIMPs (weakly interacting massive particles) has them 'orbiting' randomly and elliptically around the center (like stars in globular cluster). In these models (for some reason) dark matter is assumed not rotate like luminous matter, i. e. dark matter is not rotating en mass in roughly circular obits around the galaxy center.The radial velocity distribution information obtained from doppler provides (high quality) information about only one axis of the galaxy, so the dark matter distribution need not be spherical . It might very well be, for example, a somewhat flatten sphere called an ellipsoid.The consequence of this (if it's right!) would be that the earth is plowing through huge amounts of dark matter all the time. The earth would see a 'wind' of dark matter blowing through at (an average) 230 km/sec, which is the sun's velocity around the galaxy center. There would be a small annual modulation in the dark matter 'wind' due to a fraction of the earth's 30 km/sec velocity around the sun (earth's orbit is titled 60 degrees to the plane of the sun around the galaxy) being added, and six months later subtracted, to the sun's 230 km/sec around the galaxy center. (Current underground WIMP detection experiments are looking for this annual variation.)
There was recent report (in Scientific American 4/07) about how streams of stars protruding from the galactic plane (from galaxies in the past swallowed up by the Milky Way) can be used to probe black matter. The data (reported as confirmed by other researchers) is that the the shape of the star streams is not consistent with an ellipsoid shape for dark matter. With an ellipsoid shape of dark matter the star stream paths around the galaxy would have a corkscrew shape, but the path looks to be circular, which is compatible with a spherical distribution of dark matter.
Does dark matter
exist?
Does dark
matter really exist? Well, conventional wisdom is that dark matter
makes up most of the mass of our galaxy and most galaxies. But after 20
years of work, experimental and theoretical, no one knows what dark matter
is. The guessing is that it is an as yet undiscovered (subatomic) particle.
Neutralino --- The principal candidate for dark matter is basically a heavy neutrino. Known generically as WIMPs (weakly interacting massive particles), they interact only via the weak force (& gravity). The leading WIMP candidate for dark matter (says Nicolson and Wikipedia, which calls it an "excellent candidate") is a proposed supersymmetric particle called the neutralino.The article in Apr 07 Scientific American went on to say, "interestingly the data is consistent with MOND" (modified newtonian dynamics). This is an interesting theory that gravity vs distance relationship departs from square law when the amplitude is very low. Physicist Lee Smolin in his recent book said many physicists lie awake at night wondering if MOND might be true. With this theory of gravity the need from dark matter disappears, since it can explain the flat shape of the star velocity vs radius plots. MOND was invented in 1981 by Mordehai Milgrom, specifically for this purpose. In 2002 Milgrom wrote an article in Scientific American entitled, "Does dark matter really exist?"It's (sort of) the supersymmetric partner of the photon, Z boson, and neutral higgs combined. Of course, no one knows how heavy it is (if it exists!), but experiments (in deep mines) looking for it cover the range of 1 to 1,000 times the mass of the proton (1 to 1,000 Gev/c^2). (For some reason) it's assumed to have fairly low energy, thus it's cold dark matter. Neutrino-like underground experiments have been in progress since mid 1990's looking for rare recoils of an atomic nucleus when hit. The signatures of a WIMP hit is a variation in recoil angle (daily) and intensity (annual) that track the sidereal day (relative to stars, 4 min less than 24 hours).
In 1992 astronomers began an observing program (called MACHO) to test if the mass of dark matter halo around the Milky Way might be made up of very dim star and star-like objects. These include white and red dwarfs, compact remains of blown up stars like neutron stars and black holes, and brown dwarfs, sometimes called 'failed stars', where fusion reactions do not start because the mass is too low (< 0.08 solar mass). The idea was to look for transient brightening (due to gravitational lensing) as one of these objects passes in front of a star. Millions of stars in the Large Magellanic cloud (a large satellite galaxy of the Milky way) and the bulge of the galaxy were monitored for years. The number of brightenings (microlensings) seen has been quite low, a few dozen. The conclusion is that these type of objects are not dark matter; the upper limit of their contribution to the mass of the dark halo of our galaxy is 20%.
Type
Ia supernova --- Not so stable as thought? (2/22/2010)
The type Ia
supernova has been a very important cosmological tool. How it forms was
thought to be well understood, and crucially, unlike other supernovas,
white dwarf stars explode as a specific mass threshold is crossed. Since
the only known (meaning likely) mechanism for white dwarfs to gain mass
has them gaining mass slowly, it means that all white dwarf supernova
explosions should be virtually identical, they all have the same energy
and brightness. This is extremely useful for determining distance. In the
jargon of the astronomer a type Ia (white dwarf) supernovea explosion is
a 'standard candle', the absolute brightness of the supernova are
all the same.
Type Ia supernova underlie the two ground breaking studies about a decade ago that concluded that the universe is expanding. These studies measured and plotted the brightness of type Ia supernova brightness vs distance (red shift). At large distances type Ia supernova measured dimmer (brighter?) than expected, and from this it was concluded that the universe is expanding. Theorists posit that dark energy exists with its outward (anti-gravity) pressure is the cause of the expansion.
Why are type Ia supernova thought to be the same
The standard
picture (textbook picture) for type Ia supernova is a white dwarf star
in a tight orbit around a larger star. Computer models show the white dwarf
slowly
accrete
mass from its larger companion. When the mass of the white dwarf exceeds
the stability limit for a white dwarf star, called the Chandrasekhar limit,
the star becomes unstable and explodes. This is what a type Ia supernova
is and is the only picture I have seen given for how a white dwarf can
explode. But according to a paper in Nature (2/22/2010) there's another
way that's likely or even dominant in some galaxies. .
They propose that in elliptical galaxies, which are roundish galaxies full of redish older stars, collisions of two white dwarfs are the more likely cause of type Ia supernova. A simulation video accompanied the NYT story shows two white dwarfs orbiting and getting closer and closer, and as they merge off goes the supernovea. Elliptical galaxies are galaxies where stars individually (and perhaps chaotically) whiz in and out around the center of mass of the galaxy in elliptical orbits. Stars move this way too in circular globular clusters and in the central bulges of large spiral galaxies. Whereas in spiral galaxies like the Milky Way stars outside the central bulge orbit around the center of the galaxy pretty much traveling together in a circle or big ellipse.
The unsettling aspect, of course, is that if the ideas in this new paper are right the mass (hence energy) of all type Ia supernovas are not the same. (The article didn't mention this, but it seems obvious that the mass can vary by a factor of two as two white dwarfs just under the Chandrasekhar limit can collide.) The article says the expanding universe/dark energy experiments are not affected by this data because all their standard candle type Ia were in spiral galaxies, and they were careful to "calibrate their data" (whatever that means!) .
The new paper presents data from the new Chandra X-Ray satellite supporting their position that collisions dominate in elliptical galaxies. White dwarfs slowing accreting gas are expected to emit x-rays from the accreting gas, which gets very hot, but there would be (almost) no x-rays from colliding white dwarfs. The researchers looked at five elliptical galaxies and found only 2% to 3% of the x-rays they would expect to find with standard slow accretion model of type Ia supernova formation, hence they conclude that white dwarf collisions dominate there, placing 5% as the upper limit on accreting type white dwarf supernovas.
Caveat --- My only source of information on this so far is from a single article in NYT about the Nature article. While this article is published in the major journal Nature, it is a new idea, so it needs to be taken with a grain of salt for a while.
Microwave
background temperature
Probably the most remarkable data in physics --- Fit of the measured COBE
satellite microwave amplitude spectrum to the black body curve for 2.74
degrees kelvin. I think I read that when this data was first shown at a
technical conference the audience cheered.
The temperature measured later by the higher resolution WMAP (Wilkinson Microwave Anisotropy Probe) was 2.725K.
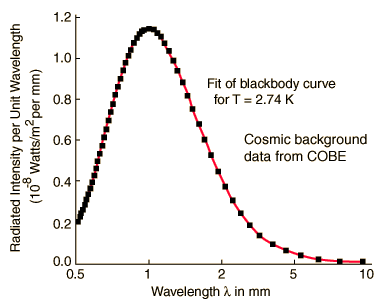
Hyperphysics site --- (they credit) Mather, J.
C., et al., Astro. Jour. 354, L37 (1990)
Big bang electron
capture
I found this
neat figure (below) in May 09 Scientific American and scanned it. It shows
in detail the sequence of how free electrons in the early universe were
captured, first by helium nuclei (one electron and then two) and later
by hydrogen. Photons interact strongly with free electrons (via thompson
scatter), so when there were lots of free electrons in the universe it
was opaque to light. The figure shows that most of the free electrons were
mopped up by about 380 thousand years (3,000 K) making the universe pretty
much transparent to photons. (Technically the mean free path of photons
grew to almost the length of the universe.) This is often referred to as
the 'decoupling' of photons and matter.
Most of the photons detected by cosmic microwave background satellites started traveling free in the orange/yellow zone (260 to 370 thousand years after the big bang). But note 10% of the free electrons were mopped up quite a bit earlier (18 thousand years) by helium nuclei. Thus it may be possible to tease some information about this earlier time from the cosmic microwave background.
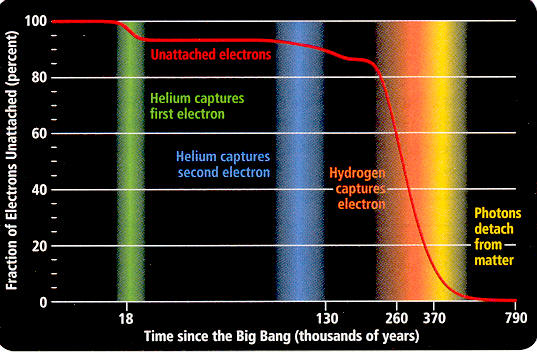
scan from May 09 Scientific American
The red shift of the cosmic microwave radiation comes from the stretching of space. Since it started off at about 3,000K and is now 2.74K, the universe has expanded since the decoupling at 380 thousand years (from the big bang) by about a factor of [1,100 = 3,000/2.74].
Size
of the universe -- now and at decoupling
(2/21/12)
Harvard physicist
says the size (linear dimension) of the visible universe is about
100 billion light-years (round numbers). Clearly this is slippery concept
since the universe is now known to be 13.74 billion years old. She only
says there is no contradiction between the two numbers because space has
expanded in the meantime. She also says parts of the universe we can see
can cannot see each other. Wikipedia ('Observable Universe) agrees and
says the radius of the observable universe is 47 billion light-years (diameter
of the observable sphere is 94 billion light-years).
I can see that we could look back 13.74 billion years one way and another 13.74 billion years in the opposite direction for a distance across of 27.4 billion light-years across. So where does the other factor of four come from? Has space only expanded by x4 from the time of the earliest quasars, this seems hard to believe.
Wikipedia -- Metric expansion of space
It is a slippery
concept. Wikipedia says this:
It is also possible for a distance to exceed the speed of light times the age of the universe, which means that light from one part of space generated near the beginning of the Universe might still be arriving at distant locations (hence the cosmic microwave background radiation). These details are a frequent source of confusion among amateurs and even professional physicists.[1] Interpretations of the metric expansion of space are an ongoing subject of debate.[2][3][4][5]Universe is huge at 'decoupling'Ref [1] -- For a (semi) readable discussion of interpretation of high red shifts see this 2003 technical paper -- http://arxiv.org/pdf/astro-ph/0310808v2.pdf
From a quick scan of the paper the flavor of the argument is something like this: A distant object at the time it emits light may be moving away from the earth (due to the expansion of space between us) at faster than the speed of light, and initially its emitted photons are also moving away from us > c. But our 'Hubble sphere', which is some sort of outer limit to which we can see, expands with time, so (the argument goes) at some point it expands enough to include some of the photon from the distant source. Those photons will eventually reach us and we will see the distant object even though it has been moving away from us faster than the speed of light always, from the moment it emitted the photons and until they reach earth.
The source of the confusion is the Hubble constant is not constant. If it had been constant over the life of the universe, then the Hubble Volume, which is the distance where objects are moving away from us at c, then this would be the most distant objects we could see. Early in the life of the universe matter was slowing down, now it is expanding. During the early slowing down phase Wikipedia ('Hubble Volume') says, "In a decelerating Friedmann universe, the Hubble sphere expands faster than the Universe and its boundary overtakes light emitted by receding galaxies". Now with an accelerating universe the Hubble sphere is shrinking faster than the universe, which is why in the distant future distant galaxies will go over the horizon and no longer be visible.What above paper makes clear is that it is incorrect to apply 'special relativity' formulas to high red shifts. When a quazar z >1 (some are at 3 meaning hydrogen frequency lines are at 1/3rd normal) the doppler interpreation says it is receeding at > c, but the authors say that is OK, we can still receive the photons. (argument is technical and beyond me) They quote many references saying the way to understand how we can see a z = 3 redshifted object is to 'special relativitity' correct the speed (red shift) so recessional velocity comes out less than c. The authors says this is all wrong. Special relativity does not apply to cosmological distances and times, general relativity applies.
Why
cosmic microwave background (CMB) looks like a surface
I have always
found it hard to think about the what we are 'seeing' when our instruments
looks at the cosmic microwave background (CMB). At 300 k years after big
bang the entire universe went from being opaque to transparent as nearly
all the free electrons were swept up by protons to form neutral hydrogen
(great 'decoupling'). So before that time everywhere in the universe it
looked like a fog. Yet Lisa Randall in her book calls the CMB we see a
"surface". It suddenly occurred to me how to think about this and
what this 'surface' means.
My idea was this. At decoupling photons start traveling from everywhere in every direction. As a (weird) though experiment let's says we are at a point in space where the Milky Way galaxy will form. Photons start out from this region of space, but we don't observe any of these photons now because they have been traveling away from us (in every direction) for the nearly the life of the universe and are now 13.74 billion light years away from us. What we see as the CMB photons all originated in a spherical shell (of the photon fog) surrounding us with a radius of 13.74 light years. (These numbers need correction for changes in Hubble constant) These are the photons arriving on earth now. This is why we see a CMB radiation as surface of a sphere with us in the center. Later checking Wikipedia I find this idea is right.
"The collection of points in space at just the right distance so that photons emitted at the time of photon decoupling would be reaching us today form the surface of last scattering, and the photons emitted at the surface of last scattering are the ones we detect today as the cosmic microwave background radiation (CMBR)." (Wikipedia 'Observable Universe')Cosmic microwave background maps (3/13)
From the spacial spectrum the Plank team derives the following properties of the universe:
"It now seems the universe is 13.82 billion years old, instead of 13.73 billion, and consists by mass of 4.9 percent ordinary matter like atoms, 27 percent dark matter and 68 percent dark energy.""The Hubble constant, which characterizes the expansion rate, is 67 kilometers per second per megaparsec — in the units astronomers use — according to Planck. Recent ground-based measurements combined with the WMAP data gave a value of 69, offering enough of a discrepancy to make cosmologists rerun their computer simulations of cosmic history."
"The data also offered striking support for the notion of inflation, which has been the backbone of Big Bang theorizing for 30 years. ... Cosmologists still do not know what might have caused inflation, but the recent discovery of the Higgs boson has provided evidence that the kinds of fields that can provoke such behavior really exist."
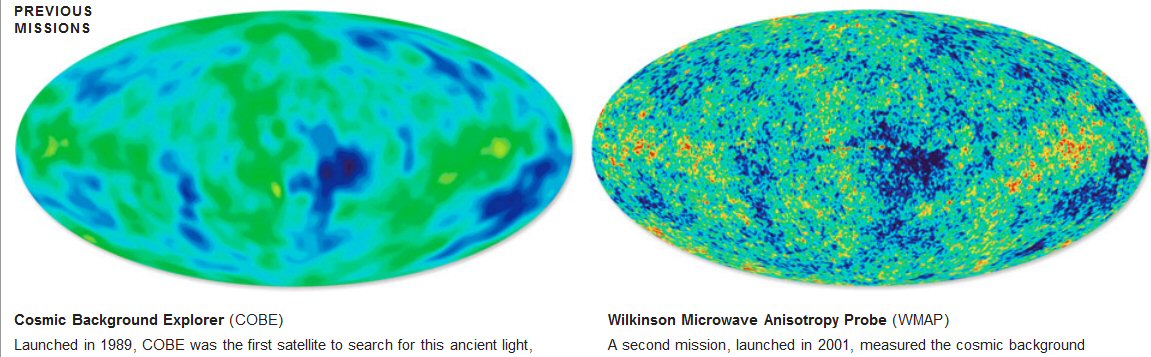
Cobe and Wilkinson satellite maps clearly match up
very nicely
(source -- http://www.nytimes.com/interactive/2013/03/21/science/space/0321-universe.html?ref=space)
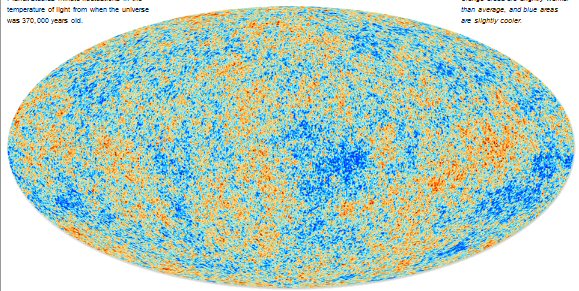
Planck satellite (2009 launch) map with x2 resolution
of Wilkinson
and fully consistent with Wilkinson and Cobe
(source -- http://www.nytimes.com/interactive/2013/03/21/science/space/0321-universe.html?ref=space)
Higgs field (3/2013)
With the official
'discovery' of the higgs boson at CERN's large hadron collider it looks
like the higgs field really exists. I have looked up the higgs field yet
in Wikipedia, but I just finished a book about the search for higgs called
'Massive'. The case for the higgs boson existing looks pretty strong. Both
large detectors individually at CERN got a 5 sigma peak, which is the gold
standard for a 'discovery', a (sharp?) peak in the data very close to each
other at 125 to 126 Gev. In addition Fermilab Tevatron in USA before it
shut down had found a broad bump in their data, consistent with higgs,
in the 115 to 135 Gev range. CERN and Tevatron had earlier ruled out a
large range of energies leaving the 110 to 130 Gev window as the last to
be explored.
The higgs boson was proposed about 50 years ago by Higgs and others. It is well understood mathematically and has been searched for decades. For a long time now it has been the only particle or boson (a force carrier) predicted by the standard model that has not been experimentally confirmed to exist. It is an unusual particle in that it has no spin, and it also has no charge or color charge.
Bosons theoretically have interger spins, but nearly all bosons have the same spin: -1. The only exceptions are higgs boson with spin of 0 the posulated graviton (force carrier of gravity) with a spin of 2. Fermions (particles) have half interger spins (-1/2, -3/2, etc). Bosons, like the photon, can 'bunch up' (think laser), but matter fermions all with spins -1/2 and can't bunch up. They take up 'space', they obey the Pauli exclusion principle (a natural repulsion), so atoms and stars exist and are stable.
CERN has confirmed its candidate higgs boson has no spin and the statistics matched the two primary ways a higgs has been calculated to decay (two photons, and W and Z weak force bosons). The channel for a rare third decay path (four leptrons) though showed nothing. The large hadron collider will be down for two years and will resume operation in 2015, this time at full power of 7 Tev.
Scalar field and
mass
While the headlines
are all about the higgs boson, what I find interesting is the higgs field.
Like its boson the higgs field is unique in that it is a scalar
field, meaning unlike E and H field it has no direction. It's though
to be a field that is present and constant everywhere in the universe.
(One CERN physicists says think a layer of snow on a field.) Seems to me
it is somewhat what is sometimes called an 'offset', a constant term that
can be added to many equations.
Some particles don't sense it, photons for example, these are particles that move at the speed of light. All other particles have mass and the theory says these particles are moving less than the speed of light, and appear to us to have mass, because they are plowing through the higgs field. The more they interact with the higgs field the more mass they have. Mathematically higher mass particles have a higher coupling constant to the higgs field.
Has
earth been plowing through the higgs field for 4.7 billion years?
Apparently. So the
obvious question is why is not the earth's orbit around the sun affected
if for 4.7 billion years it has plowing through the higgs field. Has it
slowed at least a little? No one ever mentions this. The answer I presume
is that this a quantum mechanical thing and macro objected, which theoretically
probably have some interaction, in practice sense a neglible interaction.
The history of astronomy seems to say any retarding effects of the higgs
field on astronomical objects must be very small if not completely negligible.
Higgs field vs luminiferous aether
So in 2013
we get data from which we conclude the universe is pervaded by a uniform
(presumably constant, maybe with some ripples) 'field' with no direction.
It impedes the motion of subatomic particles (without somehow bleeding
energy from the objects?), yet it has no measurable effect on massive objects
in motion, allowing Newton's law of motion to work. This sure reminds me
of the aether that 19th century scientists thought pervaded the universe.
It too was uniform and scalar and everywhere including in the vacuum of
space. It was posulated as the stuff that waved as light traveled though
the vacuum, yet the earth in orbit plowed right though it without any apparent
resistance.
from Wikipedia
On 14 March
2013 CERN confirmed that:
"CMS and ATLAS (two large detectors in the large hadron collider tunnel) have compared a number of options for the spin-parity of this particle, and these all prefer no spin and positive parity [two fundamental criteria of a Higgs boson consistent with the Standard Model]. This, coupled with the measured interactions of the new particle with other particles, strongly indicates that it is a Higgs boson. This also makes the particle the first elementary scalar particle to be discovered in nature."-- The mass of a fermion (particle) is proportional to the strength of its interaction with the Higgs.
-- Since the coupling of particles to the Higgs boson is proportional to their mass, this process (higgs creation) is more likely for heavy particles (colliding). In practice it is enough to consider the contributions of virtual top and bottom quarks. Top and bottom are the heaviest (3rd generation) quarks with the top quark much heavier than the bottom quark (172.9 Gev vs 4.2 Gev). (The heaviest 2nd generation quark is the charm quark at 1.3 Gev, while the up and down quarks, which make up ordinary matter, are only a few Mev.)
-- Since the higgs boson interacts with all the massive elementary particles of the SM (standard model), the Higgs boson has many different processes through which it can decay.
-- For a Higgs mass of 126 GeV/c2 the SM predicts that the most common decay path is into a bottom–antibottom quark pair (8.4 Gev), which happens 56.1% of the time.The second most common fermion decay at that mass is a tau–antitau pair (triple heavy electron), which happens about 6% of the time. (A higgs boson mass greater than ~346 GeV/c2, twice the mass of the top quark (172.9 Gev), would have been required to decay via top–antitop quark pair.)
-- Much rarer is the decay into a pair of photons mediated by a loop of W bosons or heavy quarks, which happens only twice for every thousand decays. However, this process is very relevant for experimental searches for the Higgs boson, because the energy and momentum of the photons can be measured very precisely, giving an accurate reconstruction of the mass of the decaying particle. (The book Massive was misleading here as it talked about this as one of two primary decay, however, it may have been one of the two primary decay routes the experimentalists were looking for.)
-- The most likely possibility is for the Higgs to decay into a pair of W bosons (the light blue line in the plot), which happens about 23.1% of the time for a Higgs boson with a mass of 126 GeV/c2. The W bosons can subsequently decay either into a quark and an antiquark or into a charged lepton and a neutrino. However, the decays of W bosons into quarks are difficult to distinguish from the background, and the decays into leptons cannot be fully reconstructed (due to the neutrino).
Wikipedia 'Higgs Field'
Here is how
Wikipedia introduces the higgs field.
-- Although apparent, mass is not generated by the Higgs field, as creation of matter or energy would conflict with the laws of conservation; it is, however, transferred to particles from the field, which contains the relative mass in the form of energy. Once the field has endowed a formerly massless particle it slows down because it has become heavier, therefore giving other particles the chance to latch onto it using the electromagnetic force.Well that's less than clear, but elsewhere in the article the argument is given more clearly. First, to preserve the conservation of energy it is assumed that the vacuum has energy (in the form of the higgs field, I guess). If a particle we know as massive enters it, then "energy from the vacuum is transferred into that particle (from the higgs field), giving it mass".
The 'higgs mechanism' Wikipedia article adds this:
-- More precisely, the Higgs mechanism endows (some) gauge bosons in a gauge theory with mass through absorption of Nambu–Goldstone bosons arising in spontaneous symmetry breaking. This mechanism may also leave behind elementary scalar (spin-0) particles, known as Higgs bosons. In the Standard Model, the phrase "Higgs mechanism" refers specifically to the generation of masses for the W±, and Z weak gauge bosons through electroweak symmetry breaking.So exactly how much energy is there in the higgs field? Presumably more than all the static mass/energy of the universe? But for some reason that question is never asked.-- Fermions, such as the leptons and quarks in the Standard Model, can also acquire mass as a result of their interaction with the Higgs field, but not in the same way as the gauge bosons.
-- The Higgs mechanism is a type of superconductivity which occurs in the vacuum. It occurs when all of space is filled with a sea of particles which are charged, or, in field language, when a charged field has a nonzero vacuum expectation value. Interaction with the quantum fluid filling the space prevents certain forces from propagating over long distances (as it does in a superconducting medium.
-- In a metal, the conductivity shields electric fields by rearranging charges on the surface until the total field cancels in the interior. But magnetic fields can penetrate to any distance. ... In a superconductor, however, electric charges move with no dissipation, and this allows for permanent surface currents, not just surface charges. When magnetic fields are introduced at the boundary of a superconductor, they produce surface currents which exactly neutralize them.
Link
A better source
of info that Wikipedia on higgs may be the site below by a particle phyistist
who has taken it on himself to try to more accurately explain higgs to
the general public.
http://profmattstrassler.com/2012/10/15/why-the-higgs-and-gravity-are-unrelated/
Cyclic universe
theory (12/1/10)
Two years
ago I read a very interesting new book by two big guns in cosmology proposing
a new theory of the universe, challenging the big bang.
Endless
Universe: Beyond the Big Bang -- Rewriting Cosmic History,
by Paul J. Steinhardt and Neil Turok
Their new theory takes a hint from string theory that unseen branes colliding may be the source of energy for the start of the universe. They conclude that our universe may be just one of an infinite series of universes. A series of universes extending over infinite time is (as I see it) a dual of current big bang thinking, which has universes extending over (speaking loosely) infinite space.
Below is my long Amazon review from two years ago (11/25/09) of the book summarizing its main points. (8 of 8 people found review useful).
***** Major challenge to the big bang theory
This is a very interesting and important book on a major new theory on how the world began. Two prominent players in physics and cosmology (Steinhardt of Princeton and Turok of Cambridge) lay out in a very readable popular science book a fundamentally new theory, which started as the Ekpyrotic universe (terrible name) in 2001 and has evolved into the cyclic universe, a theory that challenges the prevailing big bang theory. The big bang theory in its current form envisions a multi-universe with endless space of which our universe is only a tiny part. The cyclic model envisions repeating versions of a single universe spread out over endless time. In a loose sense the new theory is a 'dual'(engineering term) of the big bang with endless time replacing endless space.
If looked at in isolation, the new theory looks quite bizarre (& crazy) because it comes out of a specific string theory model with 'branes' (membranes) living in hidden extra dimensions. A lot of physicists love string theory because of its elegant mathematics and the hope it will merge merging quantum mechanics and gravity, but there is not a shred of experimental evidence supporting it. Roger Penrose (on the dust jacket) advises readers who are skeptical of string theory to "suspend such views" and read this book, adding, "It may well be closer to truth than you think." Also on the dust jacket are praise from Stephan Hawking, Martin Rees, and Brian Greene. Steinhardt admits this theory is a little crazy, but as Roger Penrose says, "Perhaps we need a crazy theory to address these things".
The authors do a good job showing that the prevailing big bang theory has over the last thirty years acquired its own considerable baggage and is now pretty weird too. Some textbook big bang models are in fact now known to be invalid, ruled out by high resolution data on the cosmic background radiation from the WMAP satellite. The current big bang theory implies eternal inflation and a multi-universe in which we just happen to live in a rare bit of space that is livable (anthropic theory). Big bang needs two types of unseen energy, inflation energy and dark energy, that are unrelated and both carefully tuned.
In the cyclic universe theory the horizon, flatness and monopole problems are all solved without the need of inflation, hence no inflation energy, dark energy does both jobs. One indication they might be on the right track, they argue, is that they didn't construct the theory around dark energy; its ability to solve two problems came as a sudden later revelation that is recounted in the book. Each cycle, which they estimate is about a trillion years, starts with a quasi-big bang, but it is not a singularity (temperatures are not infinite), so conditions are in principle calculable. The initial energy of the hot radiation comes from the kinetic energy of branes which moving toward each other and colliding in an unseen dimension.
The authors emphasize that all five experimental tests currently met by the big bang theory are met by their cyclic theory too, but crucially in a future sixth test (involving gravity waves) their theory and the big bang make very different predictions. Information about gravity waves from the big bang is encoded in the 'ripples' of the cosmic background radiation, and the authors suggest that a few more years of data collection by the WMAP (Wilkinson Microwave Anisotropy Probe) satellite might provide hints as to which theory of the universe is right. While the authors don't say so, confirmation of this theory would be a strong indication that string theorists are on the right track. As an aside, the authors throw out the suggestion (p 140) that dark matter at the center of galaxies might be due to gravity being felt from matter in an unseen dimension.
A major theoretical problem today is that calculation of the cosmological constant or dark energy (physically equivalent to vacuum energy) comes out too high by an astounding 107 orders of magnitude relative to experimental limits! The disagreement is so bad (& important) that it's often called the 'Vacuum catastrophe'. Steinhardt and Turok argue the very long time offered by countless earlier cycles might offer a solution to the vacuum catastrophe, because a very slow decay mechanism (via quantum jitter) for vacuum energy density is thought to exist. Essentially over time vacuum energy 'walks' down to a value just above zero and then hovers there, which is where we see it today.
Steinhardt and Turok claim to have a mechanism that after a trillion years of dark energy expansion of the universe causes the branes to be reset to the same initial conditions that began the previous cycle, so the system doesn't run down, each cycle is the same as the one before, the classic entropy problem of cyclic universes is solved, or so they say. But there is still the matter of energy to power each cycle, energy which goes into kinetic energy of the branes as they accelerate toward each other, some of which, when they collide, is converted into the total energy we see in our present universe. So where does this energy to power each cycle come from? I quote, "gravity is a bottomless (energy) pit .... It can decrease by a finite amount with each bounce and continue that way forever." (p 191-192). Forever? Does this pass the smell test?Two years after the above review I am reading the New York Times editorial page and what do I find, an editorial, not an op-ed, a real editorial by the NYT editors, on the subject of cosmology and touching on cyclic universes! According to the editorial (I have not read about this elsewhere) Roger Penrose is proposing that data (concentric rings, undoubtedly from a comic background satellite) could be evidence in the form of gravity waves from black hole collisions preceding the big bang. In other words we may have physical evidence that universes are cyclic!
Before the Boom (NYT Editorial, 11/30/10)
Astronomers and astrophysicists have given us insight into what happened in the first trillionths-of-a-second after the Big Bang, nearly 14 billion years ago. But the current cosmological hypothesis is that before the Big Bang there was nothing.
Now Roger Penrose, the eminent British mathematician, is arguing that there is physical evidence that may predate the Big Bang. In a recent paper, he and his co-author, the physicist V. G. Gurzadyan, describe a pattern of concentric circles detected against the universal backdrop of cosmic microwave radiation generated by the Big Bang. These circles, they say, may be gravitational waves generated by collisions of superbig black holes before the Big Bang.
The two scientists go even further, claiming that the evidence also suggests that our universe may “be but one aeon in a (perhaps unending) succession of such aeons.” What we think of as our “universe” may simply be one link in a chain of universes, each beginning with a big bang and ending in a way that sends detectable gravitational waves into the next universe.
The argument is highly controversial. But if the circles the two scientists have detected stand up to further examination — if they’re not the result of noise or instrumental error — it could radically change the way we think about our universe. And the notion is no more radical than that of some cosmologists who argue that our universe is only one in a multiverse — a possibly infinite number of co-existing, but undetectable, universes.
The question is: What do we do with these possibilities? Our answer is to marvel at them and be reminded, once again, that we live in a universe — however we define it — that contains more wonders than we can begin to imagine.Dipole in cosmic microwave radiation
T = T0 [sqrt{1 - (v/c)^2}/(1 - (v/c))]
since v<<c, T is approx
T = T0 [1 + (v/c)]
The measure (peak) amplitude of the dipole temperature is 0.0033K or (3.3 x 10^-3K), so the earth is moving at roughly 0.12% the speed of light.
v = 3 x 10^8 m/sec (3.3 x 10^-3K/2.74K)
= 3.61 x 10^8 x 10^-3 m/sec
= 3.61 x 10^5 m/sec (361 km/sec)
From below the earth is going around the sun at 30 km/sec, which is about 8% of the number above. Therefore I would think the dipole would show about a +/-8% variation in its amplitude annually. (I later did find a reference saying that published satellite dipole data has both earth around the sun (30 km/sec) variation removed and satellite motion (about 0.5 km/sec) removed.)
How fast
is the earth moving?
* The cosmic microwave background (CMB) contains a small almost perfectly
sinusoidal variation in velocity (doppler shift) vs direction, known as
the CMB dipole. This tells us how fast the the sun is moving through the
microwave background of space. The CMB dipole amplitude is about a part
in a thousand variation in temperature, which is equivalent to a velocity
of about 370 km/sec (368 +/-2 km/sec).
* Sun is rotating around the galaxy center about 230 km/sec.
* Earth is rotating about the sun about 30 km/sec.
The circumference of the earth is about 25,000 miles, and the earth rotates in 24 hours, so anyone on the equator is also spinning around the earth axis at about 1,000 miles an hour (about 0.5 km/sec).
Our local
group of galaxies (including Milky Way) is thought to be moving relative
to the CMB 627 +/-22 km/sec, and our galaxy is moving 40 km/sec toward
center of the Local Group.
Looking at these numbers means that the sun's rotation
around the galaxy (230 km/sec) is in the opposite direction from the local
group velocity.
Absolute earth
speed?
Does the cosmic
background radiation provide some sort of reference frame for the whole
universe allowing the earth absolute speed relative to the whole
universe to be measured. I found a 2003 paper from researchers in Australia
that seems to say yes. (While these guys are from a major university and
have published a book and several papers, they are pushing a new physics
theory (Process Physics) that subsumes Einstein and quantum physics, so
they are definitely not mainstream.) Interestingly they reexamine
old data (1927 and 1933) from "gas mode Michelson interferometer" experiments.
While the errors bands are pretty large the results agree nicely with the
cosmic radiation dipole speed.
1927
369 +/- 123 km/sec
1933
335 +/- 57 km/sec
COBE (1991)
365 +/- 18 km/sec
http://redshift.vif.com/JournalFiles/V10NO2PDF/V10N2CAH.pdf
Normally interferometer operate in a vacuum, but you can put gas in the chambers too, and for practical reasons (like temperature control) this was sometimes done long ago. These guys are arguing something like this: vacuum interferometers (classic Michaelson Morely) give a null because Lorenz contraction of the arms cancels out the absolute motion. (Goodstein of Cal Tech points out that Lorentz come up with the relativity equations in 1904 to specifically explain the null result of Michaelson Morely.) But when the light travels through gas, the gas index of refraction slightly slows down the light so the cancellation effects of Lorenz contraction are not complete.
Confirming (?) measurements of earth's absolute speed
I found an
interesting 2009 paper by three Columbians (discussing research done in
Columbia) presented at a conference in Peking. They ran an interferometer
for two years. They plot the interferometer fringe shifts over 24 hours
and show that the shape of the daily curve is different depending on the
month. They then calculated fringe shifts for various sun velocities, relative
to a 'preferred frame', and looked for best match using two criteria: best
correlation and minimum dispersion. The interferometer data using the two
criteria yielded:
Best correlation
365 km/sec
Minimum dispersion
366 km/sec
These interferometer speeds are almost identical to the Cobe CBM solar speed (365 km/sec), however the direction they get is like 90 different from Cobe! Their comment on same magnitude but different angle: "an open question". Their 'preferred frame' is defined "where light moves at constant speed, c, independently of direction and of the state of motion of the light emitter". In effect (I think) they are optimizing the axis and magnitude for the length contraction of the interferometer arms. Note sure what to make of this minor paper (but at a MIT sponsored conference), but they have a new approach to using interferometer data and they get an interesting result.
'Observation of a Non-conventional Influence of Earth’s Motion on the Velocity of Photons, and Calculation of the Velocity of Our Galaxy'Cable measurements
http://blog.hasslberger.com/docs/Cahill_Experiment.pdf
YouTube video showing a small interferometer (in air) working while rotating. Note the experimenter makes no effort to rule out or control for the obvious: flexing of the flimsy apparatus as it rotates.
http://www.youtube.com/watch?v=7T0d7o8X2-E&feature=player_embedded#
Where
did the earth get its organics?
A 2011 Nova
show (Finding Life beyond Earth) reports new data indicating that organics
may have delivered to the early earth by comets. This would have been during
a period called the 'late heavy bombardment', a 300 million year period
4.1 to 3.8 billion years ago. The speculated cause of the heavy comet bombardment
is a 2:1 orbital period ratio of Jupiter and Saturn. It is argued that
as they passed each other a 'pulse' between them pushed Saturn's orbit
outward, and this drove the orbits of the outer planets, Neptune and Uranus,
nuts pushing them out into the Kuiper belt, throwing the billions of comets
out there every which way.
Wikipedia ('Late Heavy Bombardment') says the 2:1 orbit resonance probably resulted from 'Gas giant migration', as Jupiter was drifting inward and Saturn was drifting outward. A temporary resonance formed between the orbits of Jupiter and Saturn, and this unstabilized the orbits of the outer solar system. Of course, there are a couple of competing hypotheses. One is the 'Fifth Gas Giant' (has its own Wikipedia page) which speculates there was another gas giant planet between Saturn and Uranus, and it got flung out of the solar system, flying out through the Kuiper belt.Is comet glycine the source of organic material on earth?
The principal investigator of the comet analysis says on the show that the glycine they found could be the source of organic material on earth. (It does have the key atoms.) Great headline --- All life comes from glycine!
Fifth
gas giant planet hypothesis
What I find
interesting about the 5th gas giant planet theory (see below) is if true,
it means the existence of Earth as a planet suitable for life depends on
one more unpredictable and random event in its history!
-- This hypothesis accounts for the survival of the inner terrestrial planets of our solar system -- Mercury, Venus, Earth and MarsLiquid water on satellites Enceladus and Europa(update Oct 2011)-- Jupiter lost angular momentum when it flung the fifth gas giant (between Saturn and Uranus) out of the solar system, (caused by a close encounter) leading Jupiter to recede from the sun's vicinity, insuring the stability and survival of the inner planets. (The exiting planet) caused turbulence within the Kuiper Belt and Oort Cloud en route out of the solar system. This may have led to intensive and numerous cometary and asteroid impacts the inner solar system, resulting in intensive cratering. This period is known as the Late Heavy Bombardment (ending about) 3.9 billion years ago.
Europa is one of the Galilean satellites of Jupiter. Wikipedia notes one of the largest bodies in the solar system (dia 3,100 km, between Pluto @ 2,300 km and Mercury @ 4,800 km). Its surface is covered with ice and below that is thought to an ocean of liquid water. Problem is to see if there is life down there means drilling through several km of ice. An investigator says on the new big Nova show on 'Is there life outside earth?' he doubts this will happen in his lifetime.
But a solution to the sampling problem may be at hand. Enceladus, a small satellite of Saturn, is sort of the Europa equivalent in the Saturn world, a gravitationally heated small satellite (300 mile dia) with liquid water. Cassini spacecraft, which was in orbit around Saturn, specifically visited Enceladus several times. It photographed the surface and with the sun to its back saw a huge line of ice jets shooting hundreds of miles into space (low gravity) coming from four 75 mile long cracks on the surface. In fact this ejected ice from Enceladus may be the souce of Saturn's E ring.
Erupting satellitesOne of the investigators on the show says, it's like Enceladus has a sign on it saying, 'Come sample me'. Enceladus probably has liquid water inside to power the ice jets. No need to land and drill, we can sample it the same way we did with the comet, just fly a probe through the ice jets. (No mention on Nova as to whether a mission is planned, but I image we will see one in the next decade.)
-- Enceladus is one of only three outer solar system bodies (along with Jupiter's moon Io and Neptune's moon Triton) where active eruptions have been observed. (Wikipedia, Enceladus)
http:www.astro.ucla.edu/~wright/intro.html
http:www.astro.ucla.edu/~wright/cosmology_faq.html
-----------------------------------------------------------------------------------------------------------------------------------------------------------
Andromeda (update 11/22/13)
Finally a
really great picture of our closest big neighbor galaxy, M31 Andromeda.
Adromeda is hard to photgraph. One reason is that it is huge in the sky,
3 degrees across, x6 wider than the moon. Most pictures of Andromeda in
visible light show show little of the structure. This one is taken (mostly)
in ultraviolet by a new satellite, and because it is in ultraviolet it
high lights the young blue giant stars, so the structure of the galaxy
arms are well outlined and the brightness of the core is reduced.
This 2012 JPL picture is taken in ultraviolet light (far and near ultraviolet)
mixed with some visable from a new satellite (Galaxy Evolution Explorer)
to bring out the young, bright, blue supergiant stars, which nicely show
the structure of the galaxy in beautiful detail.

JPL link to higher resolution versions of above image
http://photojournal.jpl.nasa.gov/catalog/PIA15416
=======================================================================
Raw notes
Galileo's arguments for Earth going around the sun
'How stupid do you have to be'
Use your little finger and arm to measure the size (angular
dia) of the moon
1 cm? to 1 m
1 cm to 2 pi x 100 cm = (1/628) x 360 degrees = (about 1/2 degree)
How many stars are visible to naked eye
How many ways can stars end
Dark matter
find figures with galaxy radial velocities
Dark energy
put in figure with data & explain methodology
standard candle --- type of supernova (matter falling onto a neutron star?)
Parameters of a black hole
black hole has no hair
how to extract energy from a black hole
falling into a black hole (big and small)
how black holes radiate energy
where elements come from
carbon? resonance fix to the solar physics mystery
inflation and the problems it solves