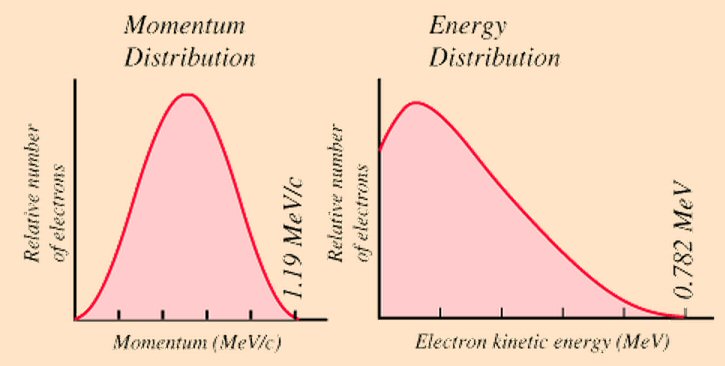
'Observed' electron energy and momentum spectrums in (free) neutron (beta) decay
source --- wonderful Hyperphysics site maintained by Rod Nave at Georgia State University
(http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html)
My related essay on 'Neutrinos' is here
Go to homepage
Atoms
How
many types
Where
do atoms come from?
Isotopes
Stability
Alpha,
beta, gamma radiation
Subatomic
particles
Size & orbitals
What
is the size of atoms?
Bohr
hydrogen radius
Helium
orbitals
Orbital
shapes
Bond
angles
Early atomic history
Thumbnail
atomic history
Fluorescence
Becquerel
'rays' from uranium
Rutherford's
alpha, beta, gamma rays
Curies
find 'extra' Becquerel rays in uranium ore
Moseley
shows how to order elements
Data
on inner electron orbits from x-rays
JJ
Thomson's tests show cathode rays are 'electrons'
How
was structure of the atom figured out?
Early
tests on atoms
alpha
particles,
seeing
an
atom decay
Spinthariscope
Alpha
emission and recoil
Beta
particle energy
Chadwick's
neutron generator
Tom Leher's song
'Elements'
First nuclear fission
Radiation in human
body
Dating
igneous rocks with radioactive potassium
Curious
facts about argon
Fun atomic calculations
History
of the atom & Introduction to Quantum Mechanics -- 2/1/11 HS talk
Somehow in my engineering training and subsequent reading I never learned much about atoms. How big are they, how was atomic structure figured out, what about isotopes? Not a clue. I know as an engineer that you can't design a machine to 'smash' atoms unless you already know a lot about atoms. So how did the early researchers probe the atom? Here is what I found out.
How many types
of atoms?
In the whole universe
there are only 92 naturally occurring elements. An element is a material
whose atoms all contain the same amount of charge. Each quanta of positive
charge resides on a heavy particle, the proton, that is part of the
nucleus in the center of the atom. Each quanta of negative charge resides
on a much lighter particle, the electron, that is part of an electron cloud
that surrounds the nucleus. Elements start at hydrogen with 1 proton, then
helium with 2, lithium with 3, and so on with no breaks up to uranium that
has 92 protons, which is the maximum number mother nature has provided.
The atomic number of an element is just the number of protons in that element's atom(s). The periodic chart is a listing of all the elements ordered by atomic number. At normal pressure and temperature some elements are solid (carbon, sulfer), some are metals (copper, gold), some are gases (oxygen, nitrogen), some are liquid (mercury, bromine).
In the nucleus of all atoms, (except hydrogen) is a second particle, the neutron. A neutron has no charge and is almost the same size and weight as a proton. The number of neutrons in an element extends over a range with the neutron count ranging from equal to, or greater than, the proton count. The different neutron count versions of the atoms of an element are called isotopes. Most elements have two or more stable isotopes found in nature.
So how many type of atoms are there? Well in terms of protons there are 92 types of atoms, but when naturally occurring stable isotopes are included the count is several times 92, or a few hundred. If all the unstable isotopes of each element that can be created are counted, then the number of different types of atoms is probably somewhere around 2,000.
Where do atoms
come from?
Atoms of elements
come (basically) from three sources: big bang, fusion in stars, supernova
explosions of stars. I am ignoring here unstable elements whose atomic
number change as they decay and a few elements made by man in particle
accelerators, nuclear reactors and nuclear bombs.
Element #1, hydrogen, is not made in stars it is consumed, so all hydrogen in the universe was created in the big bang. The big bang also created some element #2, helium, and a little of element #3, lithium.
Initially as the element # goes up the atomic mass of the element is lower than its constituent parts. This is why the nuclear reactions powering stars are fusion reactions. Reductions in mass of higher elements, relative to their constituent parts, is converted to energy via E = mc^2. For example, the rest mass of the proton, neutron, and electron are
proton
1.007276470
neutron
1.008665012
electron 0.00054858026
Hence the sum of 2 protons, 2 neutrons, and 2 electrons (minor term) is 4.0322980; but, the measured mass of helium(4) is 4.00260, which is about 0.74% less. A helium atom has to have a lower energy than its component particles, otherwise it would be unstable and would fall apart.
Our sun now 'burns' hydrogen converting it to helium. Later (in five billion years or so) it will heat up and begin to 'burn' helium (probably to element #3 lithium). In our sun elements higher than helium will not be burned because the sun does not have enough mass to get hot enough. But larger star are able to successively burn elements all the way up to element #25, manganese, yielding element #26 iron. But the element iron (? higher elements) do not 'burn' because fusing these elements requires a net input of energy. Each 'burned' element is not depleted in the burning process because much of the element being burned is too far from the hot core to burn.
Just before a large star, having burned up all the fuel in its core, has a gravity collapse and explodes as a supernova, the elements #1 to #26 are stacked up in it in rings like layers of an onion. When the star explodes, (much of) the layered elements (#1 to #26) are blown into space. However, the implosion caused by gravity and resultant rebound explosion briefly creates super high temperatures that have enough energy to cause fusion reactions to occur that need a net input of energy. This is how elements #27, cobalt, all the way up element #92, uranium, are created.
Isotopes
Many common
elements have two or three stable isotopes. Barium has seven stable isotopes
all of which occur naturally. The atomic weight (or atomic mass) of a proton
is 1.0073 and that of a neutron is 1.0087, so a neutron weighs just 0.14%
more than a proton. Different number of neutrons change the weight of an
atom, but have only a very tiny effect on the chemistry of the atom which
depends almost entirely on the electron count and structure.
Only about 0.025% of the weight of an atom is in the electrons, and neutrons weight just a hair (0.14%) more than protons, so a pretty good (within 1%) estimate of the atomic weight of an atom is just the sum of its protons and neutrons..
The link below has a listing of the atomic number and atomic weight of all elements. It shows that in every element but one (hydrogen) the atomic weight is more than twice the atomic number. This tells us that every element (except hydrogen) generally has more neutrons than protons. The official atomic weight of an element is an weighted average of the atomic weights of its stable isotopes, the average weighed by the naturally occuring frequency of each isotope.
http://www.school-for-champions.com/science/elements.htm
Stability
11 of
the 92 elements are unstable and over time (years to billions of years)
they fall apart, meaning they emit small particles from their nucleus causing
them to change into nearby elements. Up by 1 for a beta particle (electron)
emission and down by 2 for an alpha particle (helium nucleus) emission.
The top nine elements in the periodic chart, polonium (84) to uranium (92) are all unstable, meaning they have no stable isotope. Element 83 (bismuth) is right on the cusp of stability. While theoretically it decays via alpha emission to thallium (81), its recently measured life time is so huge (10^19 years) that it is for all practical purposes stable. Elements above bismuth (83) given enough time will decay to bismuth (83) or lead (82).
All the elements below bismuth have stable isotopes except technetium (43) and promethium (61). Promethium (61) is the least stable of the 92 naturally occuring elements. It's most stable isotope has a half life of only 18 years. The next least stable is technetium (43) at 4.2 mil years. The decay times of these two elements are so fast by geological time scales that (virtually) no atoms of them exist in nature.
Many naturally occuring elements exist as a mixture of isotopes, usually just two or three. In a few cases, even far down the periodic chart, one of the naturally occuring isotopes is radioactive. For example potassium-40, carbon-14, and rubinium-87 are all radioactive. Either the radioactive isotope has a very long half life so it's still around after being cooked up in stars, or it's being continuously created by some naturally occuring mechanism. Examples of the former are potassium-40 (1.26 bil years) and rubidium-87 (49 billion years). An example of the latter is carbon-14 (5,700 years), which is being continually created by cosmic rays hitting nitrogen in the atmosphere..
Uranium 92, which is well known to be radioactive, in its most stable form lasts 4.5 bil years. More specifically, uranium isotope 238 has a half life of 4.5 billion years, meaning it takes 4.5 billion years for 50% of the atoms in a sample to decay by emitting some charge, which converts it to an element lower in the periodic table. For reference, 4.5 billion years is about the lifetime of the earth and roughly 1/3 the lifetime of the universe
The intensely radioactive element radium 88 has a relatively short half life of 1,600 years, yet it can be found on Earth. In fact one ton of uranium ore contains 0.14 gram of radium, and it was first separated out and discovered to be an element in 1898 by Marie Curie. The reason an element with such a short half life exists in detectable quantities is that it continues to be made by the decay of elements above it, namely thorium 90 and uranium 92.
As Curie purified her radium samples more and more, they began to glow. When she held small quantities near her closed eyes, she saw flashes and meteors in her eyeballs. Radium puts out a lot of heat. In the early 1900's the heat output from radium samples was measured to be in the range of 134 to 140 calorie per hour/per gram.
I read somewhere --- "One quarter of the generated energy of a sample of radium comes from the decay of radium into radon gas with the remaining three quarters coming from the decay of the daughter radon (gas) atoms distributed within the sample." Is this true? Here is the radium decay chain:This means the heat from 1 gram of radium can in principle raise the temperature of 1.34 gram of water from the freezing point to the boiling point in an hour, and does so year after year, decade after decade, weaking by only 1% in about 25 years. At the time the underlying source of this heat was a total mystery. But it was experimental evidence, before Einstein came up with his famous E= m x c (squared) in 1906, that the atom must contain a lot of stored energy.radium 226 1,602 yr alpha decay @ 4.87 mev => radon 222
radon 222 3.8 days alpha decay @ 5.5 mev => polonium 218
polonium 218 3 min alpha decay @ 6.0 mev => lead 214
lead 214 27 min beta decay @ ? 1 mev => bismuth 214
bismuth 214 20 min beta decay @ ? 3 mev => polonium 214
polonium 214 180 usec alpha decay @ 7.7 mev => lead 210
lead 210 22 yrIt's pretty much true. In fact adding up the energies it looks like about 80% of the decay of a (typical) radium sample is from daughter decays. (Even though lead 210 is not stable unless the radium sample is very old (> 22 yr), most of the lead would be purified out of the sample.)
Alpha, beta,
gamma radiation
Unstable, radioactive elements (it was quickly discovered) emit three different
types of radiation: alpha, beta, and gamma. These are the first three letters
of the Greek alphabet. The naming reflects the order in which the radiation
was discovered. However, a full inventory of emitted particles also includes
the positron (anti-matter electron with a positive charge), and various
neutrinos and anti-neutrinos .
Alpha radiation
Alpha radiation is a particle made up of two protons and two neutrons,
same as a helium nucleus. Because the nucleus loses two protons, the atomic
number of the remaining atom is lower by two, while the atomic weight is
lower by four. For a given element all the alpha particles come out with
the same energy, which is high (5 Mev typ). The exit speed is typ
about 5% speed of light. The energy of the emitted particle (plus some
recoil energy of the remaining atom) can be calculated from the reduction
in total mass using E = m x c^2.
Travel in air --- Alpha particles (with a charge of 2) are highly ionizing, meaning they interact strongly with atoms (tearing out electrons), so even though they have high energy (5 Mev typ), they can travel only 2-3 cm in air (much less in solid materials). Charge is really important in how ionizing a particle is. For perspective Frisch (one of the discovers of nuclear fission) in his classic 1939 paper wrote that the two halfs of a split uranium atom, even though they have 200 Mev of energy (a huge amount), can travel on a few mm in air because their large charge of 20 or so makes them intensely ionizing.Alpha particles were widely used in early atomic research, early 'atom smashers (if you will). They were easy to build (if you had the source material) just stick a little radium or polonium in a box with a small hole. They have high energy (5 Mev typ), equivalent to an electron accelerated through five million volts. This is enough energy to penetrate and break up the nucleus of other atoms. (Rutherford fired alpha particles at nitrogen gas transmuting it to a different element.) Alpha particles also have the very useful property that (from a given source) they are all the same (same charge, mass, energy, and speed). They all exit at the same speed, because the newly created alpha is accelerated up to speed (5% the speed of light) by electrostatic repulsion between it and its birth nucleus.
Beta radiation
Beta radiation is
(historically) an emitted high speed electron. In beta decay (specifically,
beta minus decay) the usual (simplistic) picture given is that a neutron
in a nucleus converts to a proton and electron (preserving charge). The
proton stays in the nucleus, raising the remaining atomic number by one,
while the electron is emitted from the atom. Each beta (minus) decay also
emits an anti-neutrino needed to make the energy (and momentum) come out
right. Since electrons are so light, the atomic weight of the remaining
atom is (basically) unchanged.
Electrons fly outAnother type of beta decay (specifically, beta plus decay) a proton converts to a neutron, lowering the atomic number by one. A simplistic picture of this (technically not right, I think) is the creation of an electron and anti-matter electron pair from energy. The electron 'merges' with the proton to form the neutron and the anti-electron (positron) is emitted along with a neutrino. As with beta minus decay, the atomic weight is (basically) unchanged.
Clearly beta emitter materials are ejecting high speed electrons. This is how beta radiation was discovered. The electron trails can be seen in cloud chambers, but still it is a little curious. A negative beta decay adds a proton to the nucleus, so clearly for charge neutrality the atom needs to add another electron to its (outer) electron shell, yet it emits it. The obvious conclusion is that the reaction imparts to the electron much more kinetic energy than the ionization energy of the atom.
Where does the energy come from?In summary beta decay can raise or lower atomic number by one depending on whether an electron or anti-matter electron (positron) is spit out. The similarity between the two types of beta decay is clearer if this alternate (just as valid) picture of beta minus decay is used: An electron and anti-matter electron pair are created from energy. The anti-matter electron (positron) merges with a neutron (killing its 'internal electron' !), which converts it to a proton. The electron is spit out (as a beta particle).
From an energy viewpoint there something strange about a positive beta decay. A neutron has more mass than a proton and electron combined, so negative beta decay where a neutron is replaced by a proton and electron is the atom moving to a lower energy state. The loss of (rest) mass via Einstein's equation [E = m x c^2] provide a source of energy to explain where the emitted electron gets it kinetic energy. The rest mass energy of a neutron exceeds that of a [proton + electron] by 0.782 Mev (see below), which since this exceeds the rest mass of an electron (0.511 Mev), means negative beta decay has the potential to eject an electron at relativistic speeds.But in positive beta decay things are reversed. A neutron must emerge from a missing proton and electron, not to mention the kinetic energy of the emitted positron. How does this happen? Clearly an energy input is required. Where does this energy come from? What drives a positive beta reaction. As of this writing, I have no clue.
The energy released in beta decay is somewhat less than in alpha decay (typ 1-2 Mev). Unlike alpha particles the energy of beta particles from decaying elements is not uniform (for a given element), it varies continuously over a wide range. Since beta particles weigh 8,000 less than alpha particle and can have about 20% (or more) of an alpha particle energy, the fastest beta particles are traveling at relativistic speeds, in excess of 99% speed of light where their effective mass is increased by a factor of 20 or so.
Typical beta energyFor a long time the continuous variation in beta energy was not understood and quite baffling. Energy seemed to be missing, and the variation in energy seemed inconsistent with a quantized atom. It was not until the late 1930's that Fermi solved the problem with his theory of weak interactions, confirming that the missing energy was (likely) carried off by a new, as yet unseen, low mass (less mass then the electron), chargeless particle that Pauli had speculated (in 1930) might solve the problem. Fermi named the new particle the neutrino (little neutron).
Wikipedia says the typical maximum available energy in a beta decay is 1 Mev, but can range from a few kev to a few tens of Mev. The simple neutron, proton, electron rest mass calculation give only 0.782 Mev, so there must be an additional source of energy. Is this maybe an adjustment of 'kinetic energy' of the nucleons that make up the nucleus.
Continuous beta energy spectrumNeutron vs [proton + electron] energy
The energy spectrum of beta decay is described as continuous. (I heard from another source that it was Otto Hahn and Lise Meitner who had confirmed the continuous beta spectrum around 1909.) What 'continuous' here means I think is that if the energy of the emitted electrons is measured over time from a given sample of material it is found to vary smoothly (over a range).The 'explanation' given is that the (presumably well defined) maximum available energy is divided between the emitted electron/positron (kinetic energy) and neutrino/anti-neutrino energy, but for reasons I have yet to see explained (probably quantum mechanical probabilities) the energy split on an given reaction is not predictable. Since only the energy of the electron can be measured, a continuous spectrum results.
Neutron beta decayneutron 939.565 Mev/c^2
proton (-) 938.272 Mev/c^2
electron (-) 0.511 Mev/c^2
-----------------------------
0.782 Mev/c^2 neutron rest mass energy - [proton + electron] rest mass energyThe difference in rest mass energy between a neutron and proton is 1.293 Mev, the equivalent of about 2.5 electrons worth of energy (0.511 Mev), so the mass loss in a (simple) negative beta reaction provides net available energy of 0.782 Mev to share between the neutrino and kinetic energy for the emitted electron. Because the released 0.782 Mev exceeds the rest mass energy of the electron (0.511 Mev), the potential exists for the emitted electron to be accelerated to relativistic speeds. Measurements of free neutron decay, which is a simple negative beta decay, show this happens, but infrequently as usually more than half the energy is carried off by the neutrino.
In beta decay both momentum and energy are conserved in the reaction. If a stationary, free neutron was to decay ('divide') into just the two observed particles, the proton and electron, then their momentums should cancel and their kinetic energies would be expected to total to 0.782 Mev. Because the proton is so much heavier than the electron (about x2,000 times heavier), from conservation of momentum the proton 'recoils' at a very low speed. This means nearly all the released energy (0.782 Mev) should end up in kinetic energy of the emitted electron, but as the curves (above) show, when experiments are run, this is not what is found.
'Observed' electron energy and momentum spectrums in (free) neutron (beta) decay
source --- wonderful Hyperphysics site maintained by Rod Nave at Georgia State University
(http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html)
At least the measured upper energy limit of 0.782 Mev agrees with calculated energy released, but as the wonderful Hyperphysics web site (from which the above graphic comes) points out, this data is strong evidence that there must be another (unobserved) particle emitted carrying away energy and momentum, which in this case is the electron anti-neutrino. And (I presume) the neutrino here must have complementary spectrums to the electron, so the shape of the electron energy spectrum tells us that most of the more than half of the released energy ends up being carried off by the neutrino.
Why don't neutrons in nucleii of atoms decay?
Hyperphysics
give the mass of the nucleus of dueterium and tritium as follows:
dueterium
1,875.62 Mev/c^2
(vs 1,877.84 Mev/c^2 = 938.272 proton + 939.565 neutron)
tritium
2,808.92 Mev/c^2
(vs 2,817.40 Mev/c^2 = 938.272 proton + 2 x 939.565 neutron)
So why is tritium unstable?
Tritium
decays to helium 3 (stable) + electron (0.018 Mev low energy) + anti-neutrino,
but helium 3 has nucleus mass 2,809.43, which is just slightly higher
than tritium or is it 2,808.919 = 2,809.43 - .511
Curves tell us about neutrino mass
Hyperphysics points
out that we can read from the curves above that mass of the neutrino must
be zero or close to zero. This is because occasionally an electron will
be emitted carrying nearly all the available 0.782 Mev energy, so in that
case the energy of the emitted neutrino must be close to zero. Via
(E = m x c^2) this means the mass of a neutrino must be zero or close to
zero. In fact for a long time the neutrino was presumed to be a massless
particle.
Gamma radiation
Gamma radiation is (basically) high frequency, high energy light, electromagnetic
wave/photons, which travel at the speed of light. Gamma ray emissions change
neither the atomic number nor the atomic weight of the atom.
-------------------------------------------------------------------------------------------------------------------------------------------------------
Grouping of subatomic
particles
In a book
about CERN's Large Hadron Collider I came across mention of an simple way
to categorized subatomic particles. All fit within three types: leptons,
quarks, bosons.
Leptons
Point particles
with no internal structure. Only six (ignoring anti-particles). The electron
and its neutrino are closely related, both (actually electron and anti-neutrino)
occurring in beta decay. The neutrino was first postulated by Pauli (1930)
to account for missing energy, momentum and angular momentum in beta decay.
The muon and tau are unstable 2nd and 3rd generation electrons each with
their own neutrino. The muon is x207 heavier electron (2 usec lifetime),
and tau is x3,477 heavier electron (10^-13 sec lifetime).
x1
electron
(electron) neutrino
x2
muon
(muon) neutrino
x1
tau
(tau) neutrino
Lepton conservation
The neutrino is
a lepton. It has the same lepton number as the electron, which Wikipedia
says is +1. A major law in the interaction of standard model particles
is conservation of the lepton number. But how can the lepton number be
conserved if all leptons have a lepton number of +1? The answer
is anti-particles (anti-leptrons). Anti-neutrinos and the anti-electron
(positron) have a lepton number of -1.
This leads to a simple 'rule': If an electron (+1) is created, then an anti-neutrino (-1) is going to be created too. If a positron (-1) is created, then also a neutrino (+1). The rule can be extended. The neutrino only senses the weak force, so the source of the pair is likely to be the weak force carrier, a virtual boson, W+ or W-. And sure enough we find W+ decays into the positron and neutrino and W- decays into the electron and the anti-neutrino.
Quarks (hadrons)
Quarks form
composite particles grouping in three (baryons) or two (mesons). (Theoretically
particles with more than three quarks might exist, but none has ever been
experimentally found.) There are six types of quarks: (up, down), (charm,
strange), and (top, bottom). The first member of each pair ('up family')
has a change (+2/3 q) and the second member ('down family') (-1/3
q). Anti quarks have opposite charges. The very heavy top quark was not
found experimentally until 1995.
x1
up (stable)
down (decays => up)
x2
charm (decays => strange, down)
strange (decays => up)
x3
top (decays => bottom, strange, down)
bottom (decays => up, charm)
There are lots of three quark baryons of which only two are stable: proton and neutron (actually the neutron is only stable inside an atom, outside it decays in 15 min). Down quarks can decay (via W boson) into up quarks, which is how a neutron beta decays to a proton.
baryons: proton [2u (+4/3 q), 1d (-1/3 q)], neutron [1u (+2/3 q), 2d (-2/3 q)]
Since there are six quarks, they can form potentially 36 different pairs (actually they pair as a quark and anti-quark), most of which, but not all, are known to exist. All mesons are unstable. The most common are the pions (up and down quarks) and kaons (similar to pions, but with strange quark replacing down quark). As shown below the four different quark pairs that make up pions and kaons allow them to have a charge of +1, 0 or -1. They were discovered in cosmic ray experiments sixty years ago. Mesons can decay into leptons via W bosons, which can decay to a lepton. and neutrino or to an up-type quark and a down-type quark.
mesons:
pions [u (+2/3 q), anti-d (+1/3 q)]
[u (+2/3 q), anti-u (-2/3 q)] and [d (-1/3 q), anti-d (+1/3
q)]
[anti-u (-2/3 q), d (-1/3 q)]
kaons [u (+2/3 q), anti-s (+1/3 q)]
[d (-1/3 q), anti-s (+1/3 q)] and [s (-1/3 q), anti-d (+1/3
q)]
[anti-u (-2/3 q)], s (-1/3 q)]
Bosons
Bosons are
force carrying particles. Only four have been experimentally detected,
though two more are thought to exist for a total of six elementary force
carrying particles. There is one for each type of force, except the weak
force which has two, plus the Higgs boson, a major target of the Large
Hadron Collider at CERN, which is thought to give mass to particles.
The most common boson is the photon, which is absorbed and emitted by charged particles (electrons and protons) and transmits energy and momentum between them. It has zero mass, travels at speed of light and has infinite lifetime. The W and Z bosons are extremely heavy (> atom of iron) with a very short lifetime (10^-25 sec). W bosons have either negative or positive charge and are intermediates when quarks change type (changing protons to neutrons or vice versa). Z bosons have no charge, but are able to transmit changes in spin, momentum, and energy.
photon
electromagnetic
gluon
strong force
Z boson
weak force
W boson
weak force
(d quark => u quark + W boson) (W boson => e + electron anti-neutrino)
-------------
Higgs boson
(not yet detected, target of LHC at CERN)
(update) In early 2013 CERN announced the official 'discovery' of the higgs
boson, which means there is another
field in the universe, the higgs field. This is the first scalar
field, unlike, say the electric or magnetic field,
this field has no directional component.
gravitron
gravity (not yet detected)
Electron, up & down quarks
Even
though 100+ particles and anti-particle known to exist, most made in particle
accelerators and some by mother nature, nevertheless everything we see
in nature with 'our eyes' consists of only three particles: electrons,
up and down quarks.
-------------------------------------------------------------------------------------------------------------------------------------------------------
Size & orbitals
What is the
size of atoms?
Diameter
of a typical atom = 300 pm (3 x 10^-10 m or 0.3 nm)
An upper limit on the size of atoms can be estimated from very thin materials. For centuries gold has been beaten into incredibly thin layers known as gold leaf. This works because gold is malleable,in fact it is the most malleable element. The gold is layered into 'books' of parchment and beaten thinner by repeatingly hitting it with heavy hammers. Then the gold is cut into smaller squares and the process repeated over and over. Gold leaf is used to cover objects, statues, or even buildings (including dome of the MA state house). The leaf thickness is easily figured by dividing the volume of the starting gold by the area of gold leaf obtained. Gold leaf is typically 6 x 10^-7 m thick, and for a famous experiment (by Rutherford) with alpha particles fired into gold it was pounded even thinner, 6 x 10^-8 m thick or about 200 atoms thick..
An even thinner material layer is easy to made. Take 1 cubic mm of oil and drop it on a pan of water about 1 meter square. The oil will spread out to cover the whole surface. The oil thickness is (vol/area) = (10 ^-9 m3/1 m2) = 10^-9 m. This is about the thickness of one oil molecule or about 10 atoms thick. Ben Franklin was fond of doing a variation on this experiment. Franklin had the top of his cane hollowed out to hold the oil. In France he would amaze his friends by dumping the oil into local ponds where it would spread out making the pond water as flat as glass.
I tried this experiment, and clearly it only works with the right oil. Olive oil dropped into water had so much surface tension that it didn't spread at all. But one drop of 3-in-One lubricating oil spread almost instantly into a very thin layer, revealing its presence with a color interference pattern.Franklin's experiment
Franklin says, "not more than a teaspoon" of oil covered "perhaps half an acre" about 1/4 of a pond (Clapham Common Pond) on which he first ran the test. (acre = 4,047 m^2, teaspoon volume = 5 ml, 1 ml = 1 cm^3 because volume of liter = 1,000 cm^3 = cube 10 cm each side =10-3 m^3). Lord Rayleigh studying films repeated Franklin's experiment in 1890's, and we now know the oil spreads out to form a layer one molecule thick.
teaspoon oil
(cylinder 1 cm^2 x 5 cm deep) = 5 ml = 5 cm^3 = 5 x 10^-6 m^3
1/2 acre water
2,023 m^2
Oil thickness = volume /area = 5 x 10^-6 m^3/2.023 x 10^3 m^3
= 2.47 x 10^-9 m (2.5 nm)
Franklin pond reference
http://www2.avs.org/benjaminfranklin/richmond.pdf
Almost same size
Surprisingly
atoms don't vary all that much in size. A radon atom packs 86 electrons
into a sphere with only 173% the volume (120% dia) of lithium with 3 electrons.
Elements with high atomic number hold their electrons closer to the nucleus
than those with low atomic number.
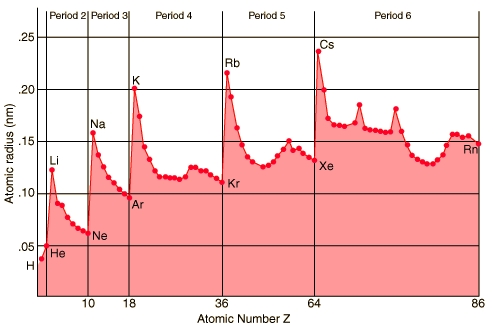
Vertical axis is radius (not diameter), so a 0.3 nm
(typ) atom diameter has 0.15 nm radius (near center of this chart)
'covalent radii' (probably) is 1/2 atomic spacing
Hydrogen is so small because in molecules its orbital
must have a lot of overlap
Bohr hydrogen radius is 53 pm (0.0.53 nm)
My atomic size sketch (update 9/10/10)
This is a
sketch I have never seen (so I drew it) showing that atoms at the bottom
and top of the periodic chart. Lithium (#3) has two electrons shells has
a radius about 2/3rds that of the highest (naturally occurring) element,
uranium #92 with seven electron shells. I drew the inner electron orbits
using the 'square rule', i.e. the radius of the inner orbit of uranium.
because it has seven shells. is 1/49th of it Wikipedia covalent atomic
radius, and lithium's is 1/4th its covalent radius.
With this assumption (approximation) the radius of the inner most electron orbit of uranium's two electrons in the 1s2 shell come out about 1/8th the radius of the inner shell of lithium (or hydrogen). As noted below the 'square rule' is somewhat of an idealization. In a calculable (fully ionized) one electron atom of uranium, the orbit of its one electron in this state would be 1/92nd that of hydrogen, because the attraction of the #92 nucleus is x92 higher than hydrogen.The marked radii in my sketch (below) are the covalent radii from Wikipedia (individual elements). The radius of quantized electron orbits in (excited) hydrogen or any ionized 'one electron' atom are known exactly because they are calculable from the Schrodinger wave equation. Hydrogen radii increase as the square of ground state radius. In other words the radii go as Ro x (1,4,9,16,25,36,49), and this is how I have sketched the orbits of uranium and lithium. I was surprised to find that the inner orbit radius of lithium (1/4th of the covalent radius) is almost exactly the orbit radius of hydrogen, which is by far the smallest size atom.
The approximation I have employed in sketch of the inner orbits of uranium and lithium is that they follow the same 'square' rule of orbits like in excited hydrogen with its single electron. Wikipedia puts this idea this way: "Orbitals of multi-electron atoms are qualitatively similar to those of hydrogen, and in the simplest models, they are taken to have the same form." (Wikipedia, 'Atomic Orbital')-- "Atomic orbitals are typically described as “hydrogen-like” (meaning one-electron) wave functions over space, categorized by n, l, and m quantum numbers, which correspond to the electrons' energy, angular momentum, and an angular momentum direction, respectively." (Wikipedia 'Atomic Orbital')
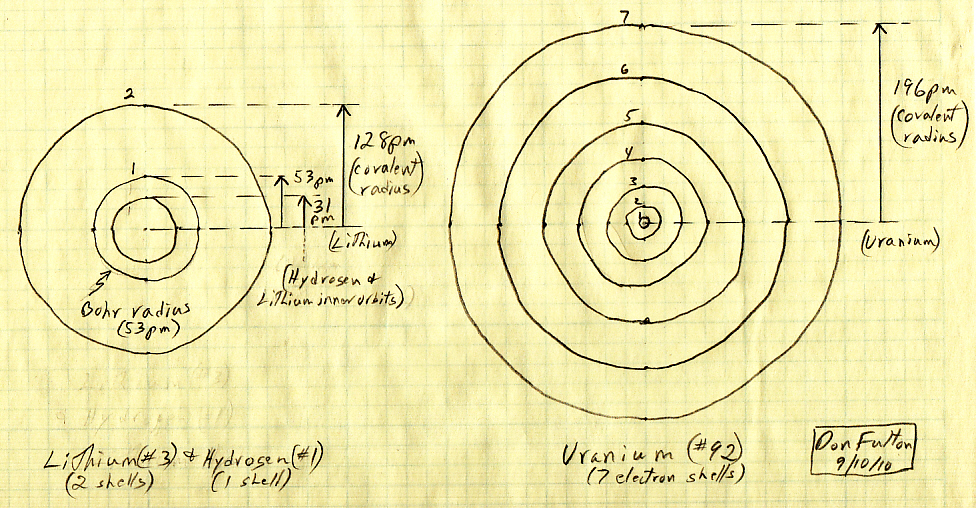
Covalent radius
Covalent radius
in obtained from measurement of bonded molecules, which means the covalent
radius of an element is often an idealized or average value. The Bohr radius
of an (isolated) hydrogen is 53 nm, yet the covalent radius for hydrogen
(Wikipedia) is given as a much smaller value 31 +/- 5 pm. It must
be that the covalent radius of bonded hydrogen, like in H2, gives a low
value because the orbitals are (substantially) overlapping, meaning 'squished'
and distorted. The Bohr hydrogen radius of 53 pm is 170% its covalent radius
of 31 pm.
In an A-A molecules, like H2, Pauling took the covalent radius to be half the center to center spacing of the nuclei. For hydrogen H-H spacing is 74 pm, so using Pauling's definition the covalent radius of hydrogen would be 37 pm (Wikipedia 'Covalent Radius'). But apparently on Wikipedia's 'Hydrogen' page an average values is used (the usual practice), because it gives the covalent radius of hydrogen as 31 pm (+/- 5), which is the value I plotted above.
Why is hydrogen so small?
An interesting question,
which I don't have the answer to, is 'Why is the hydrogen atom so small?'
Hydrogen is much smaller than all the other atoms. Specifically why does
the 2s electron in lithium (apparently) see a so much lower attractive
force than the 1s electron in hydrogen? Is some of the plotted difference
in hydrogen and lithium an artifact of how hydrogen bonds compared to lithium?
Thinking about it lithium with its low electronegativity value and the
ease in which it ionizes would (I would think) cause it to get close to
other atoms shrinking its covalent radius?? (look into this)
The orbits drawn above are really the center of electron orbital clouds which fill the space between the orbits. Wikipedia puts it this way:
"Bohr atom number 'n' for each orbital became known as an n-sphere in a three dimensional atom and was pictured as the mean energy of the probability cloud of the electron's wave packet which surrounded the atom."Wikipedia sketches of the electron orbits of lithium and uranium are below. While these sketches show the number of electrons per shell (their main purpose), clearly the inner orbit radii are not drawn to scale. The spacings between orbits are all the same.
DeBroglie wavelengths per orbit.
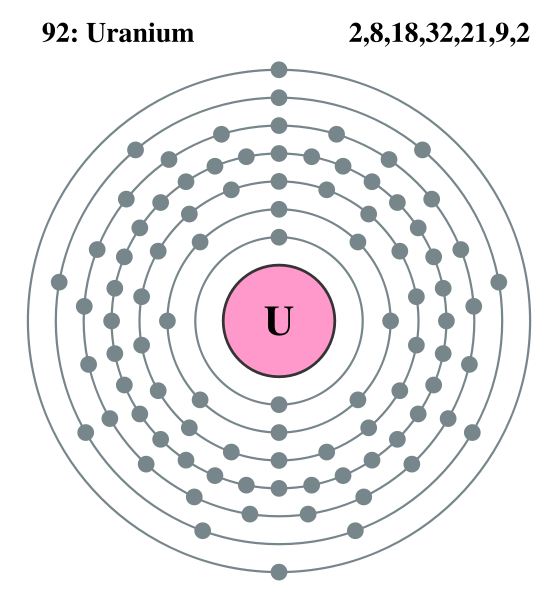
electron shells from Wikipedia Lithium ? Uranium
Quantitzation of angualar momentum
The gradual
slowing down (1/n) of electron velocity as the radius of higher orbitals
of hydrogen go up as n square (1,4,9...) also follows from (or explains)
Bohr's quantitzation of angualar momentum. When he proposed his
model, Bohr quantized angular momentum using the quantum Plank has used
earlier to model black body radiation. Angular momentum is [L = r
x P] ('r' coming in like it does in the torque eqation [Torque = r x w]).
For the circular orbits in his model Bohr said
L = r x mv = n x plank's constant (hbar)
where
n = 1,2,3.... (n is primary quantum number)
So in a ratio sense
1st orbit n=1
ro x vo = 1
2st orbit n=2
4 ro x vo/2 = 2
3st orbit n=3
9 ro x vo/3 = 3
Check -- Calculation of Bohr's radius
Quick and
dirty check can be made using the fact that v is approx 1% speed of light,
actually v = alpha x c, where alpha = (1/137) fine structure constant.
(hbar = 1.05 x 10^-34 and mass of electron = 9.1 x 10^-31)
ao x mv = 1 x hbar
(quantized angular monentum)
ao = hbar/mv
= 1.05 x 10^-34/(9.1^10^-31 x (1/137) x 3 x 10^8)
= 5.3 x 10-11 (53 pm)
Obtaining v from Bohr radius and Heisenberg uncertainty
principle
Bohr radius
(a0) is the center of the fuzzy radial width (0 to 2ao) = ao (+/- ao),
so the uncertainty in radial position can be taken as ao. Calculation is
for minimum velocity of electron so > is replaced by =. Shows speed of
electron in hydrogen is little less than 1% of the speed of light.
(delta p) x (delta x) >= hbar (1/2 appears when rms values used)
v = (hbar)/m ao
= 1.05 x 10^-34/9.1 x 10^-31 x 53 x 10^-12
= 2.19 x 10^6 m/sec = (1/137 x 3 x 10^8 m/sec)
electron velocity in hydrogen
Obtaining v from Bohr radius and De Broglie wavelength
Calculation
of 'v' from De Broglie wavelenth = (2 pi x Bohr radius = 2 pi x 52.7 pm
= 331 pm)
lamda = h/p = h/mv
(relativistically m is m x 1/sqrt{1 - (v/c)^2}
v = h/m lamda
= 6.63 x 10^-34/(9.11 x 10^-31 x 0.331 x 10^-9)
= 2.20 x 10^6 m/sec (0.0073c)
Calculation of electron kinetic energy (in eV)
E = (1/2) m v^2
= (1/2) 9.1 x 10^-31 x (2.19 x 10^6)^2/1.6 x 10^-19
= 13.6 eV (ionization energy of hydrogen)
Formula for Bohr radius
ao = (4 pi eo hbar^2)/(m e^2) = hbar/(m c alpha)
Fine structure constant
alpha = e^2/((4 pi eo) c hbar) dimensionless
Satellite check
The force
of attraction of gravity are the same as atraction of oppositely charged
particles.
Force (gravity) = G M1 M2/r^2
Force (electric) = k q1 q2/r^2 where k =1/(4 pi
eo)
Moon kinetic energy calculation
In my calculation
(another essay) for the potential energy captured as an electron slowly
is attracted to a proton to form a hydrogen atom I got 27.2 eV captured
by the electron. Half of this (13.6 eV) is radiated away (heavens are full
of 13.6 ev energy) and half (13.6 eV) kept as kinetic energy.
The same ratio should hold for the moon coming in from infinity (loosing some energy) and going into orbit about the earth. So as a check I did the calculation. Sure enough I found bringing in the moon mass (0.073 x 10^24 kg) from infinity to its present orbit (3.84 x 10^8 m) captures 7.6 x 10^28 joules, while at its mean velocity about the earth (1,023 m/sec) the moon has 3.8 x 10^28 joules of kinetic energy, exactly half of the captured potential energy. (Ref: G = 6.67 x 10^-11, Mass of earth = 6 x 10^24 kg)
E (moon in from infinity)
7.6 x 10^28 joules (captured potential energy)
E (kinetic moon orbital)
3.8 x 10^28 joules (energy converted to kinetic energy)
Electron velocity in uranium
As the charge
in the nucleus goes up the inner shells of electrons move in tighter and
go faster. How fast? In my sketch using the r goes as 'n^2' hydrogen like
orbitals, then the radial fuzz distance of the inner of seven shells would
be about 1/49 th of hydrogen, which would applying Heisenberg uncertainty,
increases the velocity x49: (This analysis is obviously approx as
it gives the same value for all elements in the 7th row of the periodic
table.)
'v' (uranium inner orbtial) = 49 x 0.0073c (hydrogen 1/137 c) (approx)
= 0.36 c (1/3rd of speed of light)
An online Q&A from a phyicist figured the inner electron velocity of uranium (element #92) this way (implying binding energy goes as Z^2):
hydrogen
v = sqrt{2 Ebinding/m} obviously this
works when Ebinding = (1/2) m v^2
= c x sqrt{ 2 x 13.6 eV/511,000 eV}
(mc^2 = 511.000 eV for electron)
= 0.0073 c
uranium
v = sqrt{2 Ebinding/m}
= c x sqrt{ 2 x 13.6 eV x 92^2/511,000 eV}
= 92 x 0.0073 c
= 0.67 c
As a ballpark figure, if uranium (element #92) has inner velocity about x100 higher than hydrogen, then its kinetic energy would be close to [13.6 ev x 10,000 = 136 kev].
X-ray data
There is hard
data that the energy levels of the inner orbits of elements way up the
periodic table and it comes from x-rays. Of interest in the x-ray spectrum
below for molybdenum (Mo, element #42) (below) are the two spikes (x-ray
'lines'). Kalpha is the n=2 to n=1 jump, and Kbeta, 16% higher in
freq, is the n=3 to n=1 jump. I calculate out the inner orbit energy and
radius here. The results
are
E inner orbital Mo
21,800 eV
Ratio to hydrogen
21,800 eV/13.6 eV = 1, 603 = 40^2
From the electron energy we can find the orbit radius using de Broglie wavelength formula.
radius = [1/2 pi] h/p = [1/2 pi] h/sqrt{2mE}
Radius inner orbital Mo
1.32 pm
Ratio to hydrogen
52.8 pm (Bohr radius)/1.32 pm = 40.0
So element #42 x-ray data tells us that elements' inner radius (goes down) and electron velocity (goes up) pretty much as Z. Why 40 and not ratio of 42? Well I eyeballed the curve to get the frequency, and Mosely's found all his data went as Z-1 rather than Z.
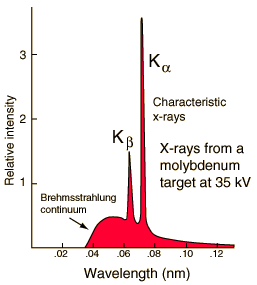
K alpha line is n=2 to n=1 jump
(source -- hyperphysics)
nth ionization data
Data on the
inner orbit energy (velocity) is also available from nth ionization data,
the ionization level for the last electron. The UK HS chemistry series
(http://www.chemguide.co.uk) says
the 17th ionization level of chlorine (element #17) is 'nearly' 400,000
kj/mol (4,145 eV). Single electron chlorine is calculable just like hydrogen,
so it will be orbiting at 1/17th Bohr radius (53 pm/17 = 3.1 pm), and should
have x17^2 higher kinetic energy (ionization energy) than hydrogen (17^2
x 13.6 eV = 3,930 eV (379,000 kj/mol), consistent with almost 400,000 statement.
Info on inside orbital energy (radius) is available from:Orbital radius goes as 1/Z
1) calculable for any single electron atom
2) measurable using x-ray narrow band radiation (n=2 to n=1 jumps)
3) measurable nth ionization data (n is element #)
E total = PE + KE
= -k e Z/r + 1/2 mv^2
where
m v r = hbar Heisenberg uncertainty
k = 1/(4 pi eo)
= -k e Z/r + (1/2) m (hbar/m r)^2
= -k e Z/r + (hbar^2/2 m) (1/r^2)
Talking the derivative of E total and setting it to zero.
0 = k e Z/r^2 - (hbar^2/m) (1/r^3)
k e Z/r^2 = (hbar^2/m) (1/r^3)
k e Z = (hbar^2/m) (1/r)
r = hbar^2/(k m e Z)
check
Wikipedia
shows the Bohr radius = (4 pi e0 hbar^2)/m e^2
Muon variation
Note, not only does
the radius shrink as Z goes up, but it also shrinks as the 'm' goes up.
An 'atom' can be made with a muon (heavy electron) orbiting a nucleus,
and since the 'm' of a muon is about 200 times higher than an electron
its ortital radius shrinks another factor of 200! I believe I read the
orbit of the muon can actually extend into the nucleus.
Alternate form of the derivatiive of energy equation
from above
0 = k e Z/r^2 - (hbar^2/m) (1/r^3)
substitute for hbar
hbar = m v r
0 = k e Z/r^2 - (m^2 v^2 r^2/m) (1/r^3)
0 = k e Z/r^2 - (m v^2)/r
Above equates attractive force [k e Z/r^2] with centripetal force [(m v^2)/r].
Ionization data
Data on energy
(velocity) of outer electrons comes from ionization data. The general principle
is that an electron in an orbital captures 2Eo when it comes in from infinity,
radiates Eo away and keeps Eo as kinetic energy. This means the ionization
energy (energy required to release an electron from an atom) is equal to
the kinetic energy of the electron. Here are some 1st ionization energies:
element #1
hydrogen
13.6 eV
element #2
helium
24.6 eV
(highest of all elements)
element #3
lithium
5.4 eV
(not lowest but quite low)
element #10
neon
21.6 eV
Helium orbitals
Hydrogen I have
calculated, but can the very high ionization energy of helium (nearly double
hydrogen) be explained? The two electrons of helium are both in the same
(spherical) orbital (spin up and spin down) as hydrogen, but is the radius
of the helium orbital also the Bohr radius? No, its further in because
for helium Z=2. A simple model, which ignores the interaction of the two
electrons, says the helium radius goes as 1/Z for Z=2 the radius of helium
should be half the Bohr radius of hydrogen.
The Bohr radius for hydrogen is 53 pm. Is the equivalent radius of helium 53/2 = 27 pm? My book The Elements (by Gray) gives only one radius for each element (without definition): hydrogen = 53 pm (Bohr radius) and helium = 31 pm.
Helium 1st ionization
If the nucleus
in helium is not shielded, then it orbital radius would be half the Bohr
radius, which would double the electron velocity, increase its kinetic
energy x4, making the helium ionization energy x4 x 13.6 eV = 54.4 eV,
but the 1st ionization energy of helium is 24.59 eV. The explanation I
think (I have not seen this explained) is that one electron must do a pretty
good job shielding the Z=2 nucleus from the 2nd electron. When the 2nd
electron is far away, it would see Z=1, and as it gets closer then shielding
of Z starts failing approaching Z=2 when in the orbital. The ionization
energy tells us the effective Z of helium as seen by the 2nd electron coming
in from infinity is {24.59 eV/13.6 eV} = 1.34 Z.
Radius from 1st and 2nd ionization data
After thinking about
this a while, it seems to me that the kinetic energy of the two electrons
in helium should be equal to the sum of the 1st and 2nd ionization
energy. After all this sum is the energy required to remove the two electrons,
and also I would think it would be equal to (1/2) the potential energy
captured by a charge of -2e coming in from infinity.
The total energy required to remove both electrons from helium is the sum of its 1st and 2nd ionization energies:
E total = 24.6 eV + 54.4 eV
= 79 eV (or 39.5 eV per electron)
This argument from the data would say that each helium electron has x2.90 = [39.5 eV/13.6 eV] more kinetic energy than the hydrogen electron. This implies a velocity higher by x 1.70 = sqrt{2.90}, which via Heisenberg Uncertainty [m v r = hbar] implies a helium radius smaller by x1.70 or [53 pm (Bohr)/1.70] = 31 pm. Yes..., this is the helium radius Gray lists in The Elements!
We can draw more conclusions. Note the 2nd ionization level of helium [54.4 eV] is exactly x4 times higher than hydrogen [13.6 eV] and is what the Schroedinger equation predicts for a one electron atom with Z=2, i.e. the radius is reduced by x2, velocity increased by x2 and kinetic energy increased by x4.
1st and 2nd orbitals of helium
So pulling
it all together the picture I find this very neat picture of the 1st and
2nd orbitals of helium: (I have derived this, not seen it in a reference!)
In helium there are two electrons (spin up and down) in the 1s orbital, but still they must be partially shielding each other from 'seeing' the full Z=2 charge of the nucleus. The result is that they orbit not at (Bohr radius)/2 = 26.5 pm with kinetic energy each of [4 x 13.6 eV] = 54.4 eV, but at the (Bohr radius)/1.7 with each electron having kinetic energy of 39.5 eV.Real radial distributionsDue to stronger shielding as one electron moves out the 1st ionization energy is not 39.5 eV, but is reduced to 24.6 eV. Note that 14.9 eV = [39.5 eV - 24.6 eV] of energy appears to be left behind, and this residual 14.9 eV must be added to 39.5 eV kinetic energy each electron originally had, so the remaining electron is left with 54.4 eV = [14.9 eV + 39.5 eV]. With the remaining electron gaining 14.9 eV in energy when the first electron kicks out, it speeds up and the radius of the one electron ionized helium tightens up a little dropping from 31 pm to 26.5 pm (exactly half the Bohr radius). And of course it now takes 54.4 eV to kick out the 2nd electron from this tighter orbit (sans shielding), consistent with the 2nd ionization level of helium.
Very neat. It really hangs together well.
hydrogen '1s' orbital radial distribution
hydrogen radial center (1) = Bohr orbit = 53 pm
 .
.
helium '1s' orbital radial distribution
helium radial center (0.59) = 0.59 x Bohr orbit =
31 pm
'Fuzzy' orbitsals also approximate
Note these radial
distributions are so broad that even saying the hydrogen orbit is 'fuzzy',
centered at 1 extending from 0 to 2, is also quite approximate, since clearly
20-30% of the hydrogen probability extends beyond 2 Bohr radii!
Ionization energy of lithium, neon
In the case
of lithium a (very) simple minded model gives us a value at least in the
ballpark. If we assume with Z=3 that the inner orbital is at 1/3rd the
Bohr radius and the second shell is x4 further out, then it would be at
4/3rd the Bohr radius. Being further out (x4/3) it's kinetic energy would
be lower than hydrogen [(3/4) ^2 x 13.6 = 7.65 eV]. Well it is in
the ballpark of 5.5 eV. (However, I recognize these lithium arguments are
mostly hand waving).
Following the same line of argument for neon at element #10 we get the inner shell now at 1/10 the Bohr radius and the 2nd shell at x4 higher or 4/10 Bohr radius, much smaller than hydrogen, and way, way off. This would produce a kinetic energy of (10/4)^2 x 13.6 eV = 85 eV. The actual value for neon is 21.6 eV.
Conclusion --- This type of simple scaling from hydrogen to other elements (even nearby one) does produce the right trend, higher in helium, lower in lithium, and higher in neon, but it's near useless at calculating the correct ionization energy!
Hydrogen orbital energy in eV
Wikipedia
('Balmer series') labels the energy jumps between hydrogen orbitals in
'nm', but I think the easy way to figure the hydrogen light energies is
to label the energy of each electron orbital in eV (see my sketch below).
The energy of the inner orbit (n =1) of hydrogen is its well known ionization
energy of 13.6 eV. The velocity of the electron falls as 1/n, so the kinetic
energy falls as 1/n^2. Since potential energy is negative and always x2
the kinetic energy, the total energy is just the negative kinetic energy.
Photons in the visible spectrum have energies between [1.65 to 3.10 eV], so only jumps with energy difference between 1.65 eV (750 nm, red) and 3.1 eV (400 nm, blue) are visible to the eye. The well known Balmer series is caused by jumps from various high orbits down to n=2, which is fairly obvious from the sketch, since the energy of the n=2 orbital is -3.4 ev. An example makes it clear how the signs work out: jump from n=3 to n=2 emits a photon with energy [-1.51 eV (higher energy) - (-3.4 eV) (lower energy)] = 1.89 eV (visible, red).
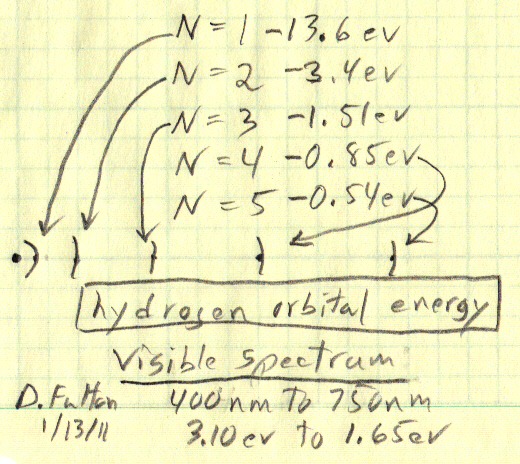
n=(1-5) hydrogen orbitals (drawn to scale, radius
increasing as n^2)
v goes down as 1/n, so kinetic energy goes down as
1/n^2

Milky Way photographed through a hydrogen-alpha filter
(source Wikipedia 'H-alpha)
Orbital filling
It's pretty
easy to figure how the orbitals fill for the first 36 elememts (#36 is
Krypton). The electrons fill so-called shells. Electrons in a shell have
(roughly) the same energy level and exist within a given radius range from
nucleus. '1' energy level goes to element #2 (helium), '2' energy level
goes to element #10 (neon), '3' energy level ('s' and 'p' orbitals) goes
to element #18 (argon), '4' energy level ('s' and 'p' orbitals) plus ten
3d orbitals goes to element #36 (krypton). There are just a few simple
rules:
* 's' orbitals
are spherical (2 electrons)
'p' orbitals have x,y,z othogonal lobes in space (6 electrons)
'd' orbitals have (more) complex shape (10 electrons)
* Electrons spread out, pairing up when no empty orbitals (at a given energy) are available, for example
B 1s2 2s2 2px1
C 1s2 2s2 2px1 2py1
N 1s2 2s2 2px1 2py1 2pz1
O 1s2 2s2 2px2 2py1 2pz1
F 1s2 2s2 2px2 2py2 2pz1
Ne 1s2 2s2 2px2 2py2 2pz2
* 'd' (block) orbitals start at shell level 3, but 4s orbitals (K and Ca) have a lower energy so fill first (as shown below)
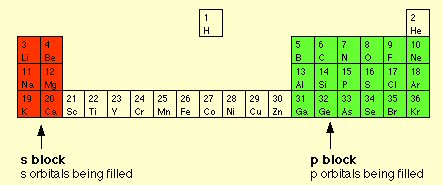
s elements (red) and (px, py, pz) elements (green)
Elements 21 to 30 have the five d orbitals filling
with pairs of electrons
(well, sort of, actually d fills 1,2,3,(no 4),5,5,6,78,
(no 9),10,10)
energy level 4 starts at element #19
source --- http://www.chemguide.co.uk/atoms/properties/elstructs.html#top
(H and He also have 's' orbitals, why they are not
red I don't know)
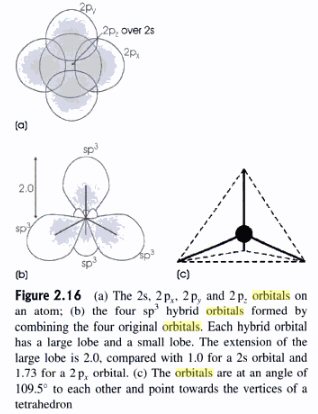
Orbital shapes (12/14/10)
Here are all
the orbital shapes. These are scans I made from a new book I bought on
the elements --- The Elements: A Visual Exploration of Every Known Atom
in the Universe", by Theodore Gray. These figures show all the orbitals
used by all elements (in ground state) even the man made ones. These
shapes come from the Schrödinger equation.
-- The Schrödinger equation, published in 1926, gave three of the four quantum numbers as a direct consequence of its solution for the hydrogen atom. This solution yields the atomic orbitals which are shown today in textbooks of chemistry. (Wikipedia 'Electron configuration')-- Although each electron in a multi-electron atom is not confined to one of the “one-or-two-electron atomic orbitals” in the idealized picture above, still the electron wave-function may be broken down into combinations which still bear the imprint of atomic orbitals; as though, in some sense, the electron cloud of a many-electron atom is still partly “composed” of atomic orbitals, each containing only one or two electrons. (Wikedia 'Atomic Orbital')
-- The electrons do not orbit the nucleus in the sense of a planet orbiting the sun, but instead exist as standing waves. The lowest possible energy an electron can take is therefore analogous to the fundamental frequency of a wave on a string. Higher energy states are then similar to harmonics of the fundamental frequency. (Wikedia 'Atomic Orbital')
-- The binding energy to contain or trap a particle in a smaller region of space, increases without bound, as the region of space grows smaller. (This conclusion comes from viewing the particle as wavepacket. As a wavepacket gets tighter, it's made up of a range of higher frequencies (lamda = h/p), so has higher velocity and energy) . (Wikedia 'Atomic Orbital')
-- Electrons jump between orbitals in a particle-like fashion. For example, if a single photon strikes the electrons, only a single electron changes states in response to the photon. (Wikedia 'Atomic Orbital')
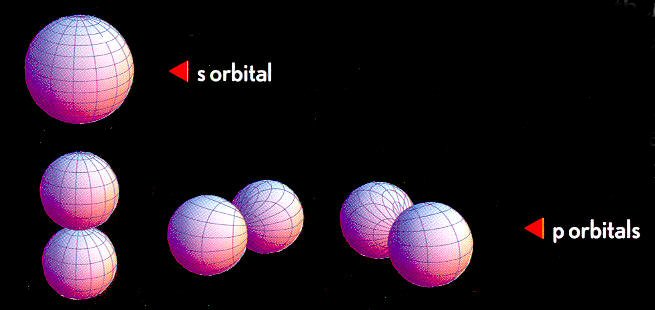
s and p orbitals
's' orbitals
are often described as 'spherical', but a radial crosssection shows complications
especially at higher energy. For example, a higher energy n = 2 's' orbit
shape of hydrogen has a double peak, a large peak at x4 radius (nom), but
it also has a much smaller peak close in.
'p' orbitals are double lobes filling space by being oriented along the x, y, z axes.
d and f orbital shapes
It's hard
to grasp the full pattern of the five d and and seven f orbitals, but some
sub-patterns are clear. In both the d and f orbitals the first looks like
a sort of rump with some of the orbits collapsed into a small collar(s)
or torus(es). The remaining four d orbits and six f orbits are drawn as
pairs. The first pair are in quadrature (like p above), but the second
pair look like they are both in the 3rd dimension and separated by 45 degrees.
Wikipedia shows that three of the four d orbitals are in fact in three planes of space like the p orbitals (xz, yz and xy planes). The 4th (quad) is in what they call an x^2 - y^2 plane and to balance this out the [double lobe + torus] orbital is aligned along the z^2 axis. Neglecting the torus the d orbits have 18 lobes [= 4 x 4 lobes + 2 lobes]. Wikipedia says these 18 lobes are arranged to fill out space as follows: 6 are on the x, y, z axis and the remaining 12 fill out the space (they give no sketch).
The best that I can visualize in my head is two flower pedals, one in the top and the other in the bottom of a cube each with with six lobes, which makes them 60 degrees apart. I suspect this is close, but not right as it is not symmetrical. (nope, see below for a better pattern) Well maybe it's not symmetrical, I have seen no statement that it is symmetrical.
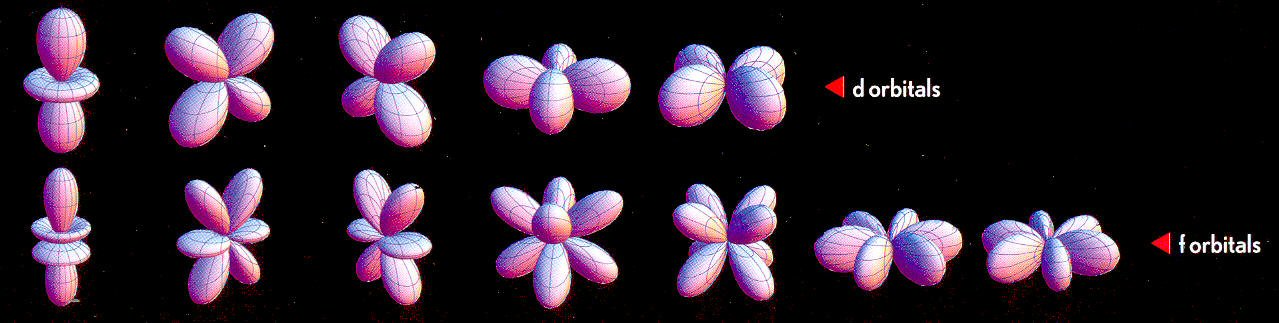
'd' (3,4 lobes) and 'f' orbitals (4,6,8 lobes)
'd' orbitals begin at n=4, element #21 (scandium)
'f' orbitals begin at n=6, first of rare earths element
#58 (cerium)
d pattern which works!
Whoooee, I see how
to map what Wikipedia says about the d orbits with the d orbits shown below.
Visualize the six lobes of the first and third sketches aligned along x,
y, z axis of a cube. The eight lobes of the 2nd and 3rd sketches then reach
out to the eight corners of the cube. So far so good, and it is still fully
symmetrical, but that leaves the 5th sketch which is aligned 45 degrees
on the x,y plane. With this included it is not symmetrical, but
if you think about it, this must be the case. There is only one
torus, so it defines a unique axis (here it's around the z axis). The 'extra'
four lobes then sqeeze into the 'not z' plane (xy plane)! This hangs together
and makes some sense.
f orbitals
The f orbits are
a more complex version of the d orbits, but seem to follow the same general
plan. The dual torus defines the z axis. There are two six lobes in the
xz and yz planes (2nd and 3rd sketches) with two six lobed groups squezed
into the 'non z' plane (6th and 7th sketch). The remaining two groups have
8 lobes (4th and 5th sketches). These then reach (sort of) for the cube
corners, but spaced apart (in quadrture?).
'n' levels and orbital shapes
I just noticed
that going up the periodic table the number of orbital shapes go up as
square of 1,2,3,4. Why?
1) 's'
4) 's' + three 'p'
9) 's' + three 'p' + five 'd'
16) 's' + three 'p' + five 'd' + seven 'f'
Each row on
the periodic table is an 'n' or energy level, and there are seven rows.
Here's how orbital shapes come in:
n = 1
s
1 orbital 2 electrons
n = 2,3
s,p
4 orbitals 8 electrons
n = 4,5
s,p,d
9 orbitals 18 electrons
n = 6,7
s,p,d,f
16 orbitals 32 electrons
What is not generally discussed and I have never seen shown is that in given shell (specific 'n', a specific energy), all the orbital shapes (as many as 16!) are (in general terms) squeezed into the same spherical volume shell of space, which must mean that they overlap to some extent (maybe to a large extent).
Adding up the electrons shows that seven shells is good up to element 118 (2 + 16 + 36 + 64 = 118).
Bond angles
Looking at
the orbitals above I though I could figure what the bond angle would be
for H2O. Oxygen is missing two electrons from its '2' energy level octet,
an octet that (when filled in neon) is two spherical electrons (2s) and
three double lobes aligned along x, y, z. (2px, 2py, 2pz). Filling
rules say 2s orbitals fill first and then an electron into 2px, 2py, 2pz,
followed by a 2nd electron into 2px, 2py, 2pz. Oxygen has six valence electrons,
so looking at the p orbitals I figured oxygen must have two empty lobes
along the y and z axis, so I guessed that when filled with hydrogen in
H2O that the bond angle would be about 90 degrees.
But when I look at water's bond angle is a slightly distorted four lobe thing with 105.9 degrees (ideally) between, so using the p orbital to predict bond angle seem to give the totally wrong answer. At this point I don't have a clue where the four lobes come from. Are the four lobes the 2px2 and 2py and 2pz lobes rearranged?
I guess a key question is --- Do the orbital diagrams (above) just have these shapes when all the orbitals in a given energy level are filled?
Whoo, now I am really confused. Reading in a chemistry book on Amazon I find this.
"In water the two hydrogen (s orbitals) form bonds with two (different) half filled p orbitals of oxygen. These oxygen p orbitals are 90 degrees to one another, so the H-O-H angle of water should be 90 degrees. " (This is what I thought in the first place!).Valence bond theory
a) Direction of the bond will be the one that gives as much overlap as
possible
b) The more the overlap of orbitals the stronger the bond
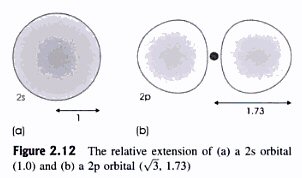
(from book 'Understanding Solids', by Richard Tilly)
The figure above (from the book) shows that each lobe of the double lobe 2px,y,z orbitals project out about 70% further (radially) than the sphrical 2s orbitals, so valence bond theory predicts that p orbitals will overlap better and will make stronger bonds than s orbitals. In water an O-H bond is the hydrogen 's' orbital overlapping one lobe of a half filled 2px oxygen orbital.
Another example in the book is the H-Cl bond in HCL. This is the 1s orbital of hydrogen overlapping with the (one) half empty 3p orbital of chlorine. "The hydrogen nucleus will lie along the x axis of the 2p (wrong!, it is the 3p) orbital since this gives the maximum orbital overlap for a give internuclear spacing." Nitrogen is between carbon and oxygen in the periodic table, so in amonia (NH3) the three 1s orbitals of hydrogen should align along the half filled px, py, and pz cartesian axes. The book adds this overlap pattern should cause the amonia molecule to look like a flattened tetrahedron.
Kicker
Now comes
the key. The books then says, "To a rough approximation these molecular
shapes are correct, but they are not precise enough" adding that the bond
angle of water is actually 104.5 degrees considerably larger than 90 degrees.
Apparently the simple orbital picture breaks down completely with carbon
(but I can't follow the argument in the book.)
Sp hybridisation orbits -- Orbitals rearrange
with further projection
Turns out
that the orbital pictures of elments (above) are pretty useless for finding
bond angles, even for simple molecules. The reason is that electrons by
gaining a little energy can move around and form completely new
orbital shapes! For example, an s and p orbital can combine (called
sp hybridisation) to form a pair of lobes as shown (below). Mathematically
this is because sums of s and p orbitals (in various ratios) are also a
solution to Schroedinger equation.
s orbitals are gone
The sp hybridisation
orbitals of the figure below (here 180 degree apart) consists of a pair
of large/small lobes. Each large/small lobe holds an electron, so the pair
of the figure (below) holds two electrons that in a non-bonded element
would be in s and p orbitals. There are several important features of sp
orbitals.
1) Large lobe projects out further than p (or s) orbitals (relative 1.93
to 2), so stronger bonds can form
2) s electrons in the valence shell shift from being in spherical orbitials
without
much projection and hence a weak ability to bond to prjecting far out and
much more likely to bond.
3) The s electrons in the valence shell are now fully equal to the p electrons
and just as likely to bond.
4) The s (spherical) orbitals are effectively gone in the case, at least
in the case where two pair of sp hybridisation lobes form (one s
electron is in each pair). (Example is carbon with four valence electrons.
Its 2px and 2py electrons hybridize with two 2s electrons to form four
identical
sp lobes making )
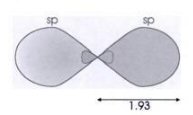
an s and p electron in reconfigured orbitals (sp hybridisation
orbitals)
(from book 'Understanding Solids', by Richard Tilly)
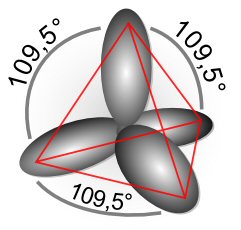
In general the number of projecting hybridisation lobes equals the number of electron orbits that combine. The book shows a pair of hybridisation orbitals, which are oriented 180 degrees, a trio which point 120 degrees, and four (carbon) which toward the vertices of a tetrahedron with an angle of 109.5 degrees. The argument is that extra energy is required to form the hybridisation orbitals, but they overlaps much more with the orbitals of atoms being joined, so on balance it is energically favorable because stronger bonds form.
The case of carbon is interesting. It has four valence electrons which in a bare atom are 2s2 and 2px and 2py. What can happen when it bonds (or so I read!) is one 2s electron moves to 2pz (then 2s and 2px,py,pz all have a single electron) and each 2p electron can combine with the same 2s electron (amazing) to form four projecting sp hybridisation lobes (since four electrons went into it). Or maybe it's just that the four valence electrons of carbon (two s and two p) 'somehow' rearrange to form four sp tetrahedral lobes! Carbon bonds to four hydrogen in methane (CH4) using these (four) tetrahedron projecting lobes.
 .
. 
carbon -- one 2s electron moves to 2p,
then three half filled 2p combine with (same, single)
2s
to form four projecting hybridisation lobes.
Example --- Carbon tetrahedron bonding in CH4 (methane)
(sources --- from book 'Understanding Solids', by
Richard Tilly
& Wiki hybridisation orbitals)
This bond picture was developed by Linus Pauling to explain molecules like methane. Methane was hard to explain given carbons electron configuration (1s2, 2s2, 2px1, 2py1). Valence bond theory would predict C would bond with two H covalently using 2px and 2py, but this molecule is very unstable. Even if one s electron upgraded to p the four bonds would not be symmetrical (s bond would be weaker due to less overlap), but this conflicts with experiments that show it takes the same amount of energy to remove any H from the carbon. The problem was how to explain carbon's four valence electrons making four identical bonds.
Pauling's sp hybridisation was the answer and is widely used for organic molecules. What is interesting is that this theory shows that in C=C (double) and carbon-carbon triple bonds not all the carbon-carbon bonds are the same. The double and tripple carbon-carbon bonds are a mixture of sp hybridisation bond overlaps and p orbital overlaps.
180, 120, 109.5 degree bond angles
Wikipedia
(hybridisational orbitals) gives the following example for double, triple
(planar) and quadruple sp hybridisational lobes.
180 degree --- BeCl2 Beryllium has two valence electrons (two s electrons) and chlorine valence shell has one half filled p orbital. The sp 'picture' here is (apparently) that the two s electrons of Be each combine with a half filled p orbital of chlorine to form two 180 lobes projecting from Be, causing BeCl2 molecule to have a linear shape. (Be has only s electrons, so either it alone form sp lobes or the s from Be and p from Cl combine to form the lobe. More hand waving?)
120 degree --- BCl3 Boron has three valence electrons (two s and one px) and chlorine valence shell has one half filled p orbital. The sp 'picture' here is (apparently) two s and one p electrons of boron reorganize into three projecting sp (single electron) lobes spaced as far apart as possible (?) (120 degrees) that each bond with a half filled p orbital of chlorine, causing BCl3 molecule to have trigonal planar (triangle) shape.
109.5 degree --- CH4 Carbon has four valence electrons (two s and px, py) and each hydrogen has a half filled s orbital. The sp 'picture' here is (apparently) both the four s and p electrons of carbon reorganize into four projecting sp (single electron) lobes spaced as far apart as possible (109.5 degrees) that each bond to an s electron of the hydrogen, causing methane (CH4) molecule to have a tetrahedral shape.
Oxygen and water
When it comes
to oxygen and it's bonding to hydrogen to make water, it seems to me valence
bond theory and sp hybridization ideas don't make a lot of sense, the picture
presented is largely hand waving. I can accept that carbon (even though
it seems unlikely) with its four valence electrons could rearrange its
s and p electrons into four identical (tetrahedral) projecting lobes. But
oxygen has got six valence electrons, not four, and yet I read (in Wiki
hybridisation of orbitals) that in water the hydrogen bond angle formed
with the oxygen derives from a basic tetrahedral shape (due to oxygen apparently)
except that the angle between the two bonded hydrogen is not the tetrahedral
109.5 degrees, but is slightly squeezed to 104.5 degrees by the four unbonded
electrons (two lone pairs). To me this picture is little more than hand
waving. How do the six electrons of oxygen from a four lobed tetrahedral
like shape? No explanation is offered, they just do!
Orbital accuracy
-- Hydrogen is the only atom for which an exact analytic solution to its Schrödinger equation is known. (Wikipedia -- Orbital hybridisation)Estimating atom size from Avogadro's number-- In heavier atoms, like carbon, nitrogen, and oxygen, the atomic orbitals used are the 2s and 2p orbitals, similar to excited state orbitals for hydrogen.
-- Hybridised orbitals are assumed to be mixtures of these atomic orbitals, superimposed on each other in various proportions.
-- Hybridisation is not required to describe molecules, but for molecules made up from carbon, nitrogen and oxygen (and to a lesser extent, sulfur and phosphorus) the hybridisation theory/model makes the description much easier.
http://invsee.asu.edu/nmodules/Carbonmod/density.html
12 grams of carbon in diamond form has a volume of (12gm/3.5gm/cm^3) = 3.43 cm^3, which is a cube 1.51 cm on a side. The dia of carbon atom can be estimated by dividing the linear dimension of the cube by the cube root of Avogado's number.
1.51
cm/{cube root (6 x 10^23)} = 1.8 x 10^-8 cm
= 1.8 x 10^-10 m (0.18 nm)
The above chart shows the radius of carbon (carbon is element 6) is about 0.08 nm, or 0.16 nm dia, so our estimate from Avogardo's number via density of carbon is pretty close with an error of only about 13%
Size of atoms from Brownian motion
In 1905 no
one knew the size of atoms. Not only that, but there was no hard evidence
that atoms even existed! What convinced everyone of the existence of atoms
and allowed their size to be calculated was a paper that Einstein wrote
in 1905 that later won him the Nobel prize. In the paper he calculated
how much a small particle would jitter (visible under a microscope) assuming
it was being continuously banged into by many tiny molecules moving with
random thermal motion.
The dancing
around of small particles, like tiny seeds, in liquid, called Brownian
Motion, had long been known but never understood. The fact that
Einstein's equation provided an accurate description of this motion was
strong proof that liquid was composed of atoms. And since the equation
he derived tied the motion of visible particles to the size of the molecules
(or atoms), it provided a way for the first time to accurately figure out
how big atoms ? molecules were.
.
Individual atoms imaged by a scanning tunneling microscope
Here is 'picture'
of silicon atoms on the surface of a crystal taken with STM, Scanning Tunneling
Microscope. It has a microprobe that generates a tiny current as the probe
passes over the electron cloud of individual atoms.
![]()
Size of nucleus
The dia of the nucleus
is 10,000 to 100,000 times smaller than the dia of the atom, on the order
of 10^-15 m. (see 'fly in cathedral' in the section 'Rutherford's alpha
recoil experiment' elsewhere in this essay).
Hydrogen ion --- Chemist talk of H+ ions in acids. For example, putting hydrogen and chlorine in water makes strong hydrochloric acid. The chlorine atoms having seven electrons in their outer shells are able to steal the electrons from hydrogen atoms, leaving Cl- and H+ ions in solution. But an H+ ion just a naked proton (isn't it?) which at 10^-15 m would be 10,000 times or so smaller than every other atom and molecule in a liquid. Also it would have an unshielded charge that would be incredible strong as one approached it (maybe this is why acids are so corrosive?). So how does this work?Riff on the 'mole'When I researched this, I found (in a textbook) the explanation that bare protons don't in fact exist in water. Water molecules are polar molecules, which means that a (partial) net charge is visible near the molecule. So what happens, the book says, is that all the 'free' protons glom onto water molecules forming H3O+ ions, sometimes called oxonium ions.
ElementsEarly atomic history
6 x 10^23 atomic weight 1 (atom of hydrogen) ?=> 1 gram
6 x 10^23 atomic weight 12 (atom of carbon) ?=> 12 gram
6 x 10^23 atomic weight 238 (atom of uranium) ?=> 238 gram
Molecules
6 x 10^23 atomic weight 18= (1 +1 + 16) (molecule of water H2O)
?=> 18 gramFrom the examples it's pretty clear what the rule is.
n grams of any pure chemical substance with an atomic weight of n (total atomic weight for all the atoms in the molecule) is called a mole and contains 6 x 10^23 (+/- 1%) molecules, which is Avogadro's number.
For technical reasons the exact definition of a mole uses carbon, so you often see the definition of a mole in terms of the 12 grams of carbon.
Thumbnail atomic
history 1897 to 1932
Thumbnail
sketch tracing how the the inside of the atom was figured out
Thomson (negative particles in cathode ray tubes), Rutherford (small positive center), Bohr (quantized electron orbits) deBroglie (electrons have wavelength which fit in Bohr's orbits) Schrodinger (develops an equation for deBroglie's wave, but doesn't know what it means), Born (suggests Schrodinger's wave equation gives probability), Heisenberg (ties it all together with his 'uncertainty' principle), Chadwick (unusually penetrating radiation from atoms). For a classroom talk a neat wrap up is would be show the class how the Heisenberg Uncertainty Principle allows the velocity of electrons in atoms to be almost trivially calculated.In the words of the the pioneers1756 Franklin -- atom size estimate
Ben Franklin shows atoms can be no bigger than 3 nm by pouring a teaspoon of oil on a pond and estimates it spreads to 1/2 acre (2,000 m^2).1900 Plank -- light emitted in quanta (by postulated 'oscillators', one quanta per cycle)
Max Plank in deriving an equation for black body radiation (spectrum of radiation vs temperature) finds he can only fit the data if he assumes light energy is emitted from oscillators, one little quantum per cycle of oscillation (E = h x freq, where 'h' is planks constant.) (1918 Nobel Prize in Physics)
--------------------------------------------------------------------------------
1897 Thomson -- cathode rays are electrons
JJ Thomson tests cathode rays finds they are negatively charged particles, always the same regardless of the trace gas he starts with, and by how much they are bent (e/m) by a voltage and thermally estimating 'm', he determines they must weigh something like 1/1000th of a hydrogen atom (1906 Nobel prize for physics)1906 Einstein -- light absorbed by electrons as quanta (with energy proportional to frequency)
Albert Einstein uses Plank's equation to explain photoelectric effect (electrons knocked off metal by light). Light appears to be absorbed by electrons only as energy quanta with the energy of the quanta proportional to the frequency (color) of the light. In this sense light looks like a lot of little particles. (1921 Nobel Prize in Physics1911 Rutherford -- positive charge is in a tiny nucleus
Ernest Rutherford (in a famous alpha recoil experiment) fires alpha particles (helium nuclei) at atoms and measures how they are deflected. Finding that most just pass through, but a tiny fraction are deflected, and a few of these actually bounce back, he concludes that all the positive charge and most of the mass of the atom must be concentrated in a tiny region in the center. Thus most of the volume of the atom is the negative electrons which must be moving rapidly so they don't fall into the postive center (to which they are attracted). (1908 Nobel Prize in Chemistry)1913 Bohr -- electron 'orbits' are quantized
Neils Bohr makes an 'ad hoc' assumption that the 'orbits' of electrons are quantized, meaning orbits are allowed only at specific radial distances. He uses the constant ('h') from Plank's light equation to quantize angular momentum [m v r = n h, where n = 1.2.3...] allowing him to calculate the orbit radii and electron energy. He finds this model of the atom is able to explain all the known line emissions of hydrogen (Balmer series of lines) as being due to energy lost or gained as electrons 'jumps' between orbits. The model also predicts new hyrogen lines and they are found. (1922 Nobel prize for physics)

(low pressure) gas emission lines
source --- PBS Brian Green's quantum physics world
(element not identified, but could be helium,
see http://jersey.uoregon.edu/vlab/elements/Elements.html)1924 de Broglie-- matter has 'waves'
Louis de Broglie in his Phd thesis suggests that electrons may have an associated 'wave'. Einstein asked to review de Broglie's thesis said, “he has lifted a corner of the great veil.” (His Phd reviewer, Max von Laue, Nobel Laureate 1914, probably jokingly supposedly says, "If this (electrons have waves) turns out to be true, I'll quit physics." He has a formula for only for its wavelength [h/mv]. It is found that de Broglie's electron wavelengths fit perfectly into the Bohr hydrogen atom forming standing waves: one wavelength in the first orbit, two in the next higher energy orbit, etc. (1929 Nobel Prize in Physics)In 1927 de Broglie's ideas were vindicated, when the Americans Clinton Davisson and Lester Germer and the Scotsman G. P. Thomson experimentally proved the wave nature of electrons: "they directed a beam of electrons on to a crystal of metal , and found that instead of bouncing off, as particles would, the electron was diffracted; just as the X-rays had been in the experiments of von Laue and the Braggs.

electrons passed through salt crystals show a classic interference pattern
(source -- http://www.launc.tased.edu.au/online/sciences/physics/debroglie.html)I know all of de Broglie's thesis is online, because I read it, but I have been unable to locate the URL again, However, I did find (below) a short 1923 de Broglie paper that appears to be an excerpt from his thesis. In it (in a very low key way) he points out that his associated electron wave for electrons in closed (constant speed) orbits will form a standing wave when the orbits have angular momentum quantized as Bohr had suggested.
So de Broglie in 1923 has recognized that his wave fits nicely with Bohr's atomic model, but surprisingly he makes no claim that this 'explains' or justified Bohr's quantization of orbit angular momentum.
http://www.davis-inc.com/physics/broglie/broglie.shtml
1925 Heisenberg -- 1st theory of quantum mechanics
Werner Heisenberg comes up with an abstract mathematical fomulation of quamtum mechanics called matrix mechanics. It does provide numbers that match experiments, but most people hate it provides no 'picture' or model to explain how electrons and light interact. (1932 Nobel prize for physics)1926 Schrödinger -- Schrödinger wave equation & 2nd theory of quantum mechanics
Erwin Schrödinger mathematically comes up with a wave equation for electrons in the atom. When solved for hydrogen, it gives all the orbital shapes ('s', three 'p', five 'd' and seven 'f') you find in see in textbooks. People like this 2nd formulation of quantum mechanics better, because physicists understand waves. Problem is: It is not clear what is 'waving' (1933 Nobel Prize in Physics)1926 Born -- de Broglie wave indicates probability
Max Born suggests that Schrodinger's and de Broglie's wave (when squared) gives the probability of finding an electron in a specific region of space. It is still not clear if the 'wave' has any physical reality. (1954 Nobel prize for physics)1927 Heisenberg -- Heisenberg 'uncertainty' principle'
-- Werner Heisenberg comes up with a simple formula that becomes a cornerstone of quantum physics. It tells what we can know, and not know, about a particle in the quantum world. Besides providing physical insight, it allows some problems, like how fast an electron moving in a specific orbit, to be simply solved. Uncertainty principle says flat out that it is impossible to know at any one time accurately both the location and motion (velocity) of an electron. [(delta x) (delta v) m > h (Planck's constant], where [(delta v) m] is then uncertainity in momentum.For example, the smaller we make an orbital (delta x getting smaller), then the faster the electron in that orbital must move (delta v getting larger) to keep the product larger than the Plank's constant. The inner electron orbital in uranium (element #92) is almost 100 times smaller (in radius) than the electron orbital in hydrogen, so according to the Uncertainty principal the inner electrons in uranium must be moving almost 100 times faster than in hydrogen, and they are, about 0.007c (0.7% speed of light) in hydrogen and 0.7c (70% of the speed of light) in uranium.
1927 -- Uncertainty principal shows electron orbits are 'fuzzy' (orbitals)
The Heisenberg uncertainty principal applied to the electron 'orbits' shows we need to consider the orbits as spread out ('fuzzed out'). The old Bohr electron orbits are just the most likely regions to find the electron, basically the center of the 'fuzz' zone.1932 Chadwick discovers neutron in nucleus
James Chadwick finds a a previously unknown particle coming out of the nucleus of the atom. Tests show is uncharged and heavy with a mass in the range of the proton.Chadwick bombards a thick layer of beryllium (element #4) with high energy, high speed (5% speed of light) alpha particles from a tiny bit of intensely radioactive polonium (138 day half life). He finds the beryllium is emitting a stream of high energy, high speed (some at 10% speed of light) particles that are uncharged. Unlike electrons these particles can travel several inches through air, are not deflected by electric or magnetic fields, and they have high mass because they are able to knock free protons (detected as a pulse of positive current) from the nuclei of many different elements. (1935 Nobel prize for physics)--------------------------------------------------------------------------------------------------------
1948 path integrals -- Richard Feynman does the 3rd formulation of quantum mechanics (path integral formulation). (1965 Nobel Prize in Physics)
http://www.spaceandmotion.com/Physics-Max-Planck.htm
Great collection of quotes about quantum mechanics
http://en.wikiquote.org/wiki/Quantum_mechanics
Fluorescence
When I was
a kid, I was fascinated by watches and alarm clocks whose hands would glow
in the dark for hours after being exposed to light. This is a property
called fluorescence that a few (non-radioactive) materials have. These
materials (somehow) absorb energy from sunlight, and then slowly (over
minutes to hours) release it as a weak glow of light.
There were a bunch of old watches in our house, and I think one or two of these may have had hands that would glow without being exposed to light. These hands have fluorescence material combined with a trace of a radioactive element to activate it. This type of watch was common in the 19th and first half of the 20th century, but are no longer made due to the fact that their hands are radioactive and to the danger in their manufacture. Curiously, there are collectors who specialize in old watches with radioactive hands even though the hands on these old watches (still radioactive) no longer glow due to the deterioration of the fluorescent material.Rontgen x-rays
x-ray of hand
taken by Wilhelm R?ntgen 1896
Becquerel 'rays'
from uranium
Becquerel
had long studied fluorescent materials (as had his father before him),
so when he heard about Rontgen's x-ray photographs and glowing tube, he
wondered if the same mechanism might be producing both the x-rays and the
fluorescence. He set about testing his fluorescent materials (he had draws
full) for x-rays using photographic plates. He would expose them to sunlight,
and then put them in the dark on photographic plates, which he later developed.
The story goes that it was cloudy in Paris for a few days and for some
reason (maybe a control run) he put his materials on photographic plates
without exposing them to light first. Most of the plates came out dark,
but one had been exposed, the one under a uranium salt fluorescent material.
Becquerel had discovered that uranium salts were continuously putting out some sort of (penetrating) ray which were different from x-rays and fluorescence. Incredibly these rays had no apparent energy source. Uranium salts appeared to be a violating the first law of thermodynamics (energy conservation)! Upon hearing of 'Becquerel rays' the Curies (in Paris) and Rutherford (at Cavendish laboratory in England) set out to investigate them.
Rutherford uses electrical conductivity of gas as a
probe
JJ Thomson,
the head of the Cavendish laboratory, had been studying the electrical
conductivity of gases when he heard about Rontgen's x-rays. Thomson confirmed
that when gas was exposed to x-rays it became much more electrically conductive.
He assigned the young Rutherford in his lab to investigate this phenomena,
and Rutherford spent two years running experiments. When Rutherford heard
about the mysterious radiation from uranium, or 'uranic rays' as Becquerel
called them, Rutherford decided to see if uranium had any effect on his
gases. It did.
Gas electrical conductivityRutherford tried attenuating the uranium radiation using very thin layers of metal. The pattern he found was that conductivity dropped as the layer were added and then it flatten out and with still with more layers started dropping again. Rutherford's conclusion was that uranium must be putting out two types of radiation (with different penetrating power), which he named alpha (most easily attenuated) and beta radiation.
An experimental setup measuring the electrical conductivity of gases turned out to to be a very useful probe for testing all the unknown rays and emanations that were discovered just prior to 1900. Rutherford as a young researcher in the best equipped physics lab in the world, Cavendish Laboratory at Cambridge, was in the right place at the right time.R?ntgen x-rays (1896), Becquerel uranium salts radiation (1896) and Schmidt's thorium radiation (1898) all lowered the conductivity of gases because (it is now known) that x-rays and the energy radiation from decaying nuclei [beta rays (electrons), alpha rays (helium nuclei), and gamma rays] all strip electrons from atoms providing free charge carriers.
Becquerel detected radiation using photographic film, but probing (unknown) radiations using gas conductivity provided huge advantages over using photographic film. For one thing gas conductivity is easily and quickly measured, and perhaps more importantly it provides a quantitative measure of of how much the radiation is affecting the gas, because it is a direct measurement of how many electrons are being stripped off the gas molecules.
Originally only uranium was known to be radioactive, but in 1898 Schmidt found that thorium was radioactive too. Rutherford tested thorium on his gasses and found out its radiation was much more penetrating than the two types of radiation from uranium. Rutherford named this (apparent) 3rd radiation type gamma rays.
Rutherford's
alpha, beta, gamma rays
Rutherford
studied the 'emanations' from uranium and other radioactive materials soon
found two components, one penetrating and one non-penetrating. The
non-penetrating component, which he named alpha rays, was stopped by thin
metal foils. The penetrating component, which sailed through the foils,
he named beta rays. He (and his team) later found a third even more penetrating
component which was related to x-rays, which he named gamma rays. So the
most common emission products of all radioactive materials were identified
and named {alpha, beta, and gamma -- first three letters of the greek alphabet}
by one man, Earnest Rutherford.
Moving charged particles in air (or vacuum) form a weak current. Magnetic fields push and pull on currents (this is how electric motors work), so applying a strong magnetic field to the rays coming out of radioactive materials can tell you a lot. If a moving particle has a positive charge, it bends one way in a magnetic field, a negative charge it bends the other way, and no charge it doesn't bend at all. How much it bends tells you something about the particles total charge, mass and velocity. (The force on the particle is proportinal to charge x velocity) Using this method Rutherford found his alpha rays (helium nuclei) had positive charge and were heavy, beta rays (electrons) had a negative charge and were light, and gamma rays had no charge (? were in fact high frequency electromagnetic rays).
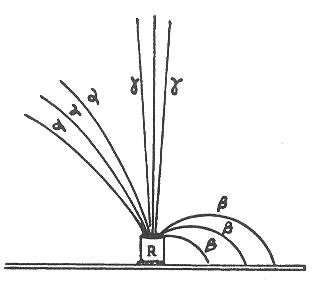
Rutherford's 1904 sketch showing trajectories
of alpha, beta, and gamma particle/rays curving in a magnetic field (to
scale?). Force vector is q(vel cross B), so B field in this sketch is pointed
into the paper. (scan from book Great Physicists by Cropper)
I'm pretty sure there is not enough information in this experiment (bending alone) to sort out particle charge, mass, and velocity. The equations are these:
accel = force/mass
magnetic force = charge x vel x B (magnetic field)
sideways distance = 1/2 accel x time^2
The time available to move sideways would be inversely proportional to the particle velocity
sideways distance = 1/2 accel x time^2
= 1/2 (force/mass) x time^2
= {1/2 x (charge x vel x B)/mass} x k/vel^2
= 1/2 x k x charge x B/(mass x vel)
So sideways motion is (roughly) proportion to the particle charge and inversely proportional to its mass and speed (momentum). The beta particle compared to the alpha particle has 1/2 charge, x20 speed (99% speed of light compared to 5% speed of light), and x20 (relativistic mass increase)/8000 mass. Multiplying this out
beta distance ratio (to alpha) = 1/2 x 1/20 x 400
= 10
Our simple calculation (assuming constant force) tells us that electrons are more easily deflected, but surprisingly less than I first guessed based on the large mass ratio of 8,000 to 1. There are two reason for this. One, (high energy) beta particles are moving about 20 times faster than alpha particles, and two, their relativistic speeds increase their mass by a factor of 20 or so. I had at first assumed Rutherford's sketch could not be to scale, but maybe it is.
Note, the term 'beta particle' in its modern usage refers both to positrons and electrons. A positron is an anti-matter electron, or (if you will) a positive electron . It has exactly the same mass an an electron but the opposite charge.Radon is found by Rutherford
This gas turned out to be the new element radon. Radon is a chemically inert gas belonging to the helium argon family. The isotope of radon that thorium creates (though a decay chain) is Rn 220, which has a half life of about 1 minute, consequently it was hard to study. Radium decay created a longer lasting (hence easier to study) isotope of radon (Rn 222) with a half life of (about) four days. Radon decays into heavy radioactive metals (solid residue on the glass) ending with stable lead.
Historically what was important about the discovery of radon was that it was the first element known to be created by 'transmutation' from another element. A new element came into being that was far more radioactive than its parent. Soddy later wrote, 'Rutherford, this is transmutation!' Rutherford's reply was, 'For heavens sake, Soddy, don't call it transmutation. They'll have our heads off as alchemists.'
Curies
find 'extra' Becquerel rays in uranium ore
The Curies
(Pierre and Marie) in Paris started to work on Becquerel rays about the
same time as Rutherford in England. While Rutherford was studying the nature
of the emanations coming out of uranium ? thorium, the Curies were
digging deep in uranium ore looking for compounds even more radioactive
than uranium or thorium.
They started
down this path when they noticed that a specimen of pitch-blende (one of
the ores of uranium oxide) was four times more active than oxide of uranium
itself. It was immediately clear to them that there must be small quantities
of a much more radioactive material in the ore. However, it took several
years of chemical separation starting with seeral tons of material to separate
it out. In the end they found not one, but three new radioactive elements:
radium (# ), polonium (#) and atinium (#
-- Marie goes systematially throuth the periodic chart looking for becquerel rays and soon finds that thorium is radioactive too. So of all the known elements only unanium and thoriun were found to be radioactive.
-- Marie finds that the level of radiation depends not on the chemical compound being tested, but only on the amount of uranium (or thorium) it contains. This was important. If radioactivity didn't depend on the arrangement of the atoms in a molecule, it must therefore be linked to the interior of the atom itself. She had found that radioactivity was an atomic property not a chemical property.
-- They found that the strong activity came with the fractions containing bismuth or barium
-- At the end of June 1898, they had a substance that was about 300 times more strongly active than uranium. In the work they published in July 1898, they write, "We thus believe that the substance that we have extracted from pitchblende contains a metal never known before, akin to bismuth in its analytic properties. If the existence of this new metal is confirmed, we suggest that it should be called polonium
-- After another few months of work, the Curies informed the l'Acad?mie des Sciences, on December 26, 1898, that they had demonstrated strong grounds for having come upon an additional very active substance that behaved chemically almost like pure barium. They suggested the name of radium for the new element.
-- Pierre, who liked to say that radium had a million times stronger radioactivity than uranium, often carried a sample in his waistcoat pocket to show his friends. Marie liked to have a little radium salt by her bed that shone in the darkness. When it turned out that one of his colleagues who had worked with radioactive substances for several months was able to discharge an electroscope by exhaling, Rutherford expressed his delight.
-- In 1903, Marie and Pierre Curie were awarded half the Nobel Prize in Physics. Henri Becquerel was awarded the other half for his discovery of spontaneous radioactivity. In 1911 she was awarded the Nobel Prize in Chemistry
-- An associate of Marie Curie, Debierne has since separated a. third radioactive substance belonging to the group of the rare earths, actinium. Actinium was discovered (1899) by Andr?-Louis Debierne in pitchblende residues left after Pierre and Marie Curie had extracted radium. Actinium was discovered (1899) by Andr?-Louis Debierne in pitchblende residues left after Pierre and Marie Curie had extracted radium The chemical behavior of actinium is similar to that of the rare earth lanthanum.
How was radioactivity measured?
The study
of radioactivity required that there be a way to measure (at least in a
relative sense) the activity (strength or level of emanations) of radioactive
materials. This is how decay times of materials were determined, which
was one of the few means of identifying radioactive materials. It was also
central to the Curies searching through components of uranium ore
for new, highly active, radioactive materials. In the early days (around
1900) there was no geiger counter or similar ionization meter. You could
see (alpha) ionization flashes in a few materials, but this was not suitable
to measure radioactivity levels. So how was it done?
It was done with the electrometer. The electrometer is a very old instrument. It was used by Ben Franklin 150 years earlier. An electrometer measures charge, and when connected to a capacitor it measures the voltage on the capacitor. A classic electrometer is two gold leafs that are electrically connected at the top and (when uncharged) hang down side by side. When it is connected to a voltage, charge flows in (into both leafs) and the leafs to fly up and away from each other due to the electrostatic repulsion of similar charges. In effect the angle of the leafs measures (approx) the amount of charge, and if connected to a capacitor the voltage on the capacitor (Q = C V).
The procedure --- The Curies placed the radioactive material (to be tested) on the inside surface one of the two plates of a capacitor. A textbook capacitor is two parallel plates, which when charged has a voltage and electric field between the two plates. The capacitor was connected to a sensitive electrometer designed by Pierre Curie and charged (by briefly connecting it voltage), and then isolated (disconnected it from the voltage). A well made capacitor can hold a voltage and charge for a long time. However, putting radioactive material inside a capacitor makes it 'leaky allowing it to self-discharge.
The key to measuring the level of radioactivity was to measure the rate at which the voltage on the capacitor decreased. The equation of a capacitor is i = C dv/dt, so the rate of change of voltage is proportional to the (ionization induced) discharge current, proportional to the level of radioactivity. The radioactive material, by briefly ionizing (make conducting) little paths of air between the two plates, allowed a weak current to flow between the plates. The more intense the radiation the higher the discharge current and the faster the capacitor voltage fell. In other words with an intensely radioactive material the electrometer leafs fell quickly, and with a weakly radioactive material the leafs fell slowly.Note in the early days there was no calibration of these instruments, but it didn't really matter. As long as the instrument was stable, i.e. it worked the same way every time, it could be used for relative measurements. If the Curies noted that batch A discharged the capacitor four times faster than batch B, they would say batch A was four times more radioactive than batch B. Similarly Rutherford to find a radioactive half life just had to periodically sample his material and plot the relative capacitor discharge times. The time it took for the capacitor discharge time to double, meaning the radioactivity level had decreased 50%, was the material half life.
-- I likewise examined certain minerals. I found, as I expected, that the minerals of uranium and thorium are radioactive; but to my great astonishment I discovered that some are much more active than the oxides of uranium and of thorium which they contain. Thus a
-- We readily
proved that pitch-blende contains very radioactive substances, and that
there were at least three. That which accompanies the bismuth extracted
from pitch-blende we named Polonium; that which accompanies barium from
the same source we named Radium; finally, M. Debierne gave the name of
Actinium to a substance which is found in the rare earths obtained from
the same ore.
-------------------------
Moseley shows
how to order elements
Moseley in
1913 found the x-ray frequency of elements rose as the square of the his
(proposed) ordering, based on atomic number. Below Moseley plots the square
root of element x-ray frequency vs an integer number, which he argues is
very likely the number of electrons/protons in the element. When plotted
this way, all his data fell nicely on a series of straight lines.
Moseley's 1913 procedure --- Elements were put inside a cathode ray tube and hit with cathode rays (high speed electrons). This causes most elements to radiate in the x-ray region. The x-rays take the form of a wide spectrum plus a few bright peaks; it was the frequency of the bright peaks that interested Moseley. The x-rays were passed through a slit and directed at a high quality crystal, whose atoms were known to be arranged in a cube, and the reflected x-rays then exposed a photographic plate. Bragg, an x-ray specialist, had recently shown that the interference pattern of x-rays reflected from a crystal face allowed the frequency of the x-rays to be accurately measured. By photographing the x-rays reflected off the crystal over a range of angles the interference pattern was revealed, and from this the frequency of the x-rays could be accurately calculated (his data has frequency to four decimal places). (I extracted this summary of Moseley's procedure from a few comments by Cropper and Moseley's 1913 paper, see link below.)His clean, well ordered data provided strong evidence that his ordering of the elements was correct and that the nature of an element is determined by its atomic number, i.e. the number of protons/electrons, not by its atomic weight. Significantly he found some gaps in his sequence, suggesting missing elements (later found). Notice there is no element shown on the vertical axis at: 43 (technetium), 61 (promethium), ? 75 (rhenium). These are three elements I never heard of!
Whoops, about a year ago I learned about technetium (#43) and promethium (#61) when I wrote the section on element stability for this essay. The reason Moseley didn't test these two elements is that they don't exist in nature. They are the only two elements down deep in the periodic chart, elements below bismuth (# 83), that are unstable. The original quantity of them inherited by the earth is long gone, and since they are not part of the decay chains of the high end unstable elements, no more has been made in nature.Moseley found the line from elements 20 to 30 could be described by the following equation:
Freq = k x (1/1 -1/2^2) x (Z -1)^2
where
k = Rydberg's constant (13.6 eV)
Z = atomic #
This equation was very suggestive, because not only was it similar to Balmer's formula, which described the visible spectrum lines of hydrogen and had recently been explained by Bohr's model of hydrogen, but also the constant in Moseley equation (k = (Rydberg's constant) came out to be exactly the same as the constant in Balmer's formula. [Why the scaling came out to be (Z-1)^2 rather than Z^2 initially puzzled both Moseley and Bohr.]
Rydberg's constant turns out to be 13.6 eV, the ionization energy of hydrogen, and also equal to the kinetic energy of its electron. The term [(1/1 -1/2^2) = 3/4] describes a jump from n=2 to n=1 orbit. Inner orbit (n=1) total energy is -13.6 Ev and n=2 orbital energy is - 3.4 eV (1/4th of 13.6 eV), so the photon energy is [- 3.4 eV - (-13.6 eV) = 10.2 eV] (or 3/4th of the n=1 kinetic energy).Moseley also showed that placement of a few elements in the periodic table of the time, which was based on atomic weights, were probably incorrect, for example, nickel (element 28) and cobalt (element 27) were reversed. Up to this time only atomic weight had been available to order elements. (Atomic weights were determined by the chemists from chemical reactions. For example, 16g oxygen (one mole) reacts with 40g calcium, 88g strontium, or 137g barium. So if oxygen used as the reference, then Ca/Sr/Ba are assigned atomic weights of 40, 88, and 137 respectively.) Since Moseley's time all periodic charts have been based on atomic number.
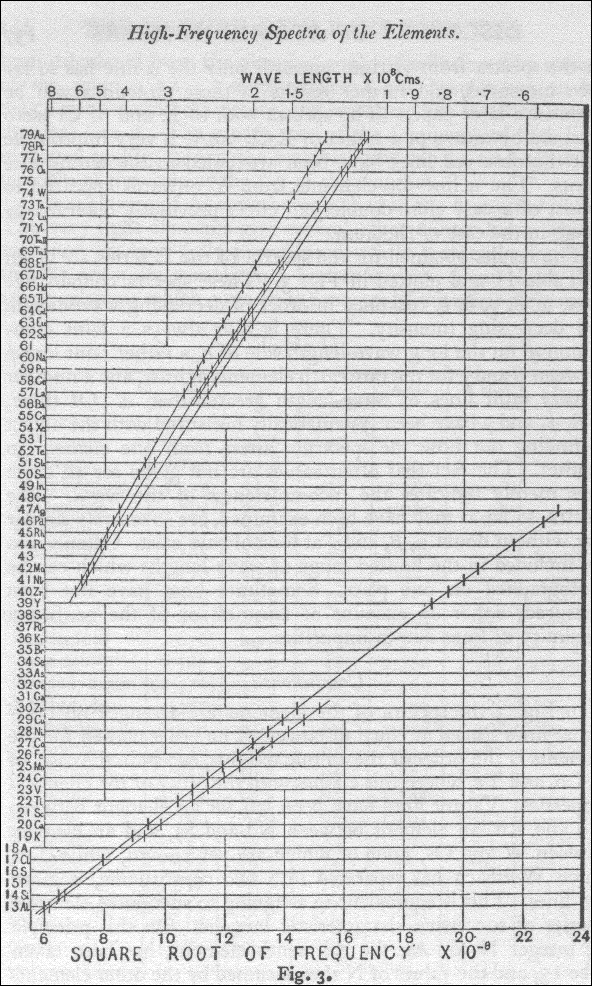
Moseley's plot of sqrt{x-ray peak frequency} vs (proposed)
atomic number for elements (13 to 79)
(data from Henry Moseley's 1913 paper "High Frequency
Spectra of the Elements")
(Moseley's hor axis scaling is confusing. The x-ray
frequency at his element 41 is 400 x 10^16 hz.
Sqrt{400 x 10^16} x 10^-8 = '20' his hor axis label
at element 41)
Here's a link to Moseley's 1913 paper (from which I got the plot above):
http://chimie.scola.ac-paris.fr/sitedechimie/hist_chi/text_origin/moseley/Moseley-article.htm
From section below we see the emitted frequency of jumps from the n = 2 orbit to inner (n = 1) orbit are expected to be proportional (3/4 th) to the inner orbit energy. Bohr one electron atom analysis predicts that inner orbit energy should vary as Z^2, so based on this K alpha x-ray frequency should rise as Z^2, or (put another way) the sqrt{K alpha x-ray frequency} should rise as Z.
So what Moseley did was to plot, for every element he could get his hands on, Z vs sqrt{K alpha x-ray frequency}. Do the data fall on a straight line? They do, very nicely. The slope of the line then indicates the power relationship between freq and Z. Is it two? As I read Moseley's data, I get element 21 at sqrt{freq} =10 and element 41 at sqrt{freq} = 20. This is a ratio of 41/21 =1.952, which is pretty close to two (2.4% off).
Why (Z-1)?Data on inner electron orbits from x-rays
Moseley says his x-ray energy (h x freq) data fit an empirical formula that scales (3/4 x 13.6 ev) of hydrogen by (Z -1)^2. Hyperphysics says the implication for the -1 is that one electron in an inner orbit appears to be shielding the nucleus, reducing the positive charge by -1 as seen by the 2nd electron jumping into the inner orbit. Clearly the formula doesn't work right for hydrogen, predicting the ridiculous value of zero. Wikipedia says the shielding effect of the inner electron, requiring the (Z - 1)^2 scaling, becomes apparent for elements higher than aluminum (element 13). Moseley plotted data is for element 14 and higher.Astronomers routinely use [h x freq = (3/4) 13.6 ev (Z-1)^2], now known as Moseley's law, to connect measured x-ray frequencies to the radiating element.
X-ray data (like Moseley collected) provides experimental evidence of the properties of inner orbits of elements. Below shows the x-ray spectrum emitted by element 42 (molybdenum) when hit by high energy electrons (figure from Hyperphysics site). The broad spectrum is braking or 'bremsstrahlung' radiation emitted by the electrons as they slow down. The peaks are called 'characteristic x-rays' and are due to electrons changing orbits. The K alpha peak is though to be radiation from electrons jumping from n = 2 orbits down to the inner n = 1 orbits into holes created by the incoming high energy electrons knocking out inner electrons.

K alpha is a jump n = 2 to n = 1 (inner) orbit of
molybdenum
(Hyperphysics site)
Footnote #1 --- K alpha x-ray emissions are seen in astronomy. Iron radiates its K alpha line when it spirals into a black hole.In any orbit the kinetic energy of the electron is equal to the lost potential energy (coming in from infinity). Whoops, not really! It's a little subtle. A calulation shows the potential energy decrease (from zero at infinity) is twice the kinetic energy of the orbiting electron. In all orbits KE=Eo and PE=-2Eo, so total E is -Eo. This makes the total electron energy the negative of its kinetic energy, which is important to explain why higher orbits have higher energy even as the electron moves slower. The formation of hydrogen captures 27.2 eV of potential energy with 13.6 eV retained as kinetic energy and 13.6 eV radiated away. We can check this using hydrogenFootnote #2 --- Medical and scientific x-rays are (mostly) K alpha x-rays, and they are generated by the same method that Moseley used in 1913, accelerate electrons and slam them into metals.
hydrogen velocity
alpha c = c/137
E potential
- 2 x 13.6 ev
E (kinetic hydrogen) = (1/2) m v^2
= (1/2) 9.11 x 10^-31 x (3 x 10^8/137)^2
= 2.18 x 10^-3 x 10^-15
= 2.18 x 10^-18 joule x [1ev/1.6 x 10^-19 coulomb]
= 13.6 ev
check
In a Bohr single electron atom say the electron in the inner orbit (n=1) has Etotal = -Eo = [KE = Eo + PE = -2Eo]. In the 2nd orbit (n=2) the electron moves at half speed, so Etotal = -Eo/4 = [KE = Eo/4 + PE = -2 Eo/4]. So the energy radiated when an electron jumps from n=2 to n=1 is due to the potential energy going more negative and comes out to be equal to 3/4th of the kinetic energy of the inner orbit [-Eo/4 (n=2) - (-Eo) (n=1) = 3/4 x Eo].
Analyzing the x-ray data
Let's works some
numbers. Reading from the figure the K alpha line of element 42 (molybdenum)
is at 0.076 nm. (Note confirmation that K alpha is a jump from n = 2 to
n =1 comes from K beta at 0.064 nm or 84% of K alpha. K beta is consistent
with being a jump from n = 3 to n = 1, since (3/4)/(8/9) = 84 %.)
Figuring the inner orbit energy of molybdenum
E inner orbit = (4/3) h freq = (4/3) h (c/wavelength)
= (4/3) 6.63 x 10^-34 x 3 x 10^8/7.6 x 10^-11
= 3.49 x -15 joule x [1 ev/1.6 x 10^-19 coulomb]
= 2.18 x 10^4 ev
Electrons accelerated by 35 kv have, of course, 3.5 x 10^4 ev of energy, so that's consistent with being able to eject an inner electron from molybdenum. Knowing the inner orbit energy we can find the electron de Broglie wavelength, which divided by (2 pi) is the orbit radius.
molybdenum inner orbit radius = [1/2 pi] de Broglie
wavelength
= [1/2 pi] h/p
= [1/2 pi] h/sqrt{2mE}
= [1/2 pi] 6.63 x 10^-34/sqrt{2 x 9.11 x 10^-31 kg 3.49 x 10^-15 j}
= [1/2 pi] 6.63 x 10^-34/sqrt{63.5 x10^-46}
= [1/2 pi] 6.63 x 10^-34/7.97 x 10^-23
= 0.132 x 10^-11 m
A Bohr orbit calculation for a one electron 'atom' of atomic number Z finds that the inner orbit radius goes down as 1/Z and energy goes up as Z^2. Since molybdenum is element 42, if it had one electron we would expect its electron orbit to be 42 times smaller than hydrogen. The Bohr radius of hydrogen is 5.29 x 10^-11 m, thus the Bohr hydrogen orbit radius ratioed to the inner radius of molybdenum, as figured from its K alpha x-ray data above, is
hydrogen Bohr radius/calculated molybdenum (element 42) inner radius
5.29 x 10^-11 m/0.132 x 10^-11 m = 40.0
The inner orbits in real high Z atoms are not going to come out exactly as a one electron Bohr calculation since (for one thing) the electrons interact. The fact that the inner orbit size calculated from the x-ray data is within 5% of the Bohr high Z one electron calculation is pretty interesting and good confirmation (I would say) that the interpreting K alpha radiation as a jump from the 2nd orbit (n = 2) to the inner orbit (n =1) is probably right.
From Heisenberg uncertainty an electron trapped in an orbit 40.0 times smaller than hydrogen should have momentum (and velocity) x40.0 higher. Since electron velocity in hydrogen is a little less than 1% c (c/137), the electron speed in molybdenum comes out at 29% c, which says there is a small error in using de Broglie non-relativistic formula. Since the inner hydrogen orbit has 13.6 ev of kinetic energy, we can do a check on our calculated inner molybdenum energy and radius. The molybdenum inner orbit electron (kinetic) energy should be higher than in hydrogen by the square of radius ratio. Is it?
(40.0)^2 x 13.6 ev (hydrogen) = 1,600 x 13.6 ev
= 2.18 x 10^4 ev vs 2.18 x 10^4 ev (molybdenum)
checks
Crossed wires?
After writing
above, I found that the K alpha wavelength of the (Hyperphysics) figure
above, which I used in the analysis, may be slightly off. Hyperphysics
in text says the K alpha line of element 42 (molybdenum) has wavelength
of 0.0722 nm (Wikipedia has similar values), but in the figure above the
K alpha line is clearly not at 0.0722 nm. I read it as 0.076 nm,
which is 5% longer. (Looks like somebody has their wires crossed.)
JJ
Thomson's tests show cathode rays are 'electrons'
In the mid
1890's JJ Thomson of the Cavendish lab investigated the nature of the cathode
rays by building several specialized Crookes tubes. The Crookes tube had
first been built by William Crookes in 1870 and over the intervening years
had slowly improved. A Crookes tube is basically a long evacuated glass
tube that has two electrodes (anode and cathode) that make a beam of cathode
rays. When high voltage is applied to the electrodes, the residual gas
in the tube between the electrodes glows. If a hole is put in the anode,
a narrow beam of 'something', called cathode rays, appears to exit through
the hole and flows in a straight line down the tube. The end of the glass
tube is coated with a fluorescent paint that glows where the beam hits
it.
JJ Thomson crookes tube with voltage deflection plates
(yellow region)
left end: high voltage causes residual hydrogen gas
in tube between anode and cathode to glow.
hole in anode passes a beam of 'cathode rays' down
the tube.
right end: spot on fluorescent paint glows when hit
by cathode ray beam
(source -- Wikipedia JJ Thomson)
In the mid 1890's the nature of the cathode rays was not understood. It was not known whether it was a type of light or particle. Wikipedia says that prior to Thomson it was known that the beam was affected by a magnet (magnetic field), but no electrostatic (E field) deflection had been seen. Thomson built the tube above and pulled a better vacuum that previous investigators. Before pulling the vacuum he filled the tube with hydrogen gas, so the small amount of gas remaining, which the voltage on the electrodes excited, should be hydrogen.
Wikipedia explains that at this time Crookes tubes were 'cold cathode'. Meaning that there was no hot cathode to boil off electrons as in all modern tubes, so the voltage needed on the electrodes (left) to get the gas ionized (glowing) was high, which means the light electrons were accelerated to high speed.When Thomson applied a voltage to the plates (right), it caused the beam to deflect toward the plate that was positive, and the amount of deflection was proportional to the voltage. The beam acted like it carried a negative charge. Thomson built another tube with an electrometer in it, and this showed charge and the beam went together, because the electrometer only showed a (charge) response when the beam hit it. Maxwell's equations had been around for 35 years, so it was known and could be calculated how a voltage and magnetic field would affect a moving beam of charged particles of mass 'm' and charge 'q'.
Force = q(E + vel cross B)
Thomson also did deflection tests with magnetic fields. From his deflection tests he could see that the beam particles had some mass, so the beam was not a form of light. He found the mass was small, something like 2,000 times less than the mass of a hydrogen atom. In an introductory (online) MIT chemistry lecture describing Thomson's experiments the professor said that with very high deflection voltages Thomson could also see a second spot that deflected just slightly in the opposite direction of the electrons. Her implication was this was probably due to positive hydrogen ion, but I am dubious since if electrons are accelerated rightward, then positive ions should be accelerated leftward.
At the time atoms were thought to be the most fundamental unit of matter, but JJ Thomson by 1897 had good evidence for a particle that appeared to originate from a hydrogen atoms and had a mass that was a tiny fraction of the mass of the hydrogen atom, so for this he gets credit for discovering the electron. The Wikipedia quotes Thomson on his conclusions:
"As the cathode rays carry a charge of negative electricity, are deflected by an electrostatic force as if they were negatively electrified, and are acted on by a magnetic force in just the way in which this force would act on a negatively electrified body moving along the path of these rays, I can see no escape from the conclusion that they are charges of negative electricity carried by particles of matter." (J. J. Thomson)As to the source of these particles, Thomson believed they emerged from the molecules of gas in the vicinity of the cathode.
"If, in the very intense electric field in the neighborhood of the cathode, the molecules of the gas (hydrogen) are dissociated and are split up, not into the ordinary chemical atoms, but into these primordial atoms, which we shall for brevity call corpuscles (later called electrons); and if these corpuscles are charged with electricity and projected from the cathode by the electric field, they would behave exactly like the cathode rays." (J. J. Thomson)Below is a link to a paper by Thomson about these experiments. In it he discusses how he got obtained values for the velocity of the beam (approx 3 x 10^7 m/sec or 10% of speed of light) and the ratio of m/e (10^-7). What he did was measure the radius of curvature of the beam and the temperature rise of a thermometer the beam hit, which provides an estimate of the kinetic energy of the beam.
http://web.lemoyne.edu/~GIUNTA/thomson1897.htmlWikipedia and MIT talk about him estimating the mass of the electron at about 1/2000 of the hydrogen atom, but I don't see this in his paper. He knew the particle was light, which is what was important, but there was uncertainty on how much charge it carried (ratio of m/e). He could not separate low 'm' from high 'e', and he says there are reaons why 'e' might be high. My guess is that the data gave the approx 2,000 to 1 ratio if e was assumed to be the minium charge. Let's check his measured m/e = 10^-7 with the known charge of an electron (don't know if was known in 1897, but it probably was).
m = 10^-7 x e = 10^-7 x 1.6 x 10^-19 coulomb = 1.6 x 10^-26 (units ??)
Modern value for electron mass is 9.1 x 10^-31 kg (approx 10^-27 grams) and proton mass is 1.6 x 10^-27 kg. Units are always tricky with old papers, but if the mass above is in grams, then it is in the ballpark, within a factor of six of the correct value.
How was structure of the atom figured out?
Atomic history 1900 to 1920's (medium to long, a series
of talks)
Thumbnail sketch tracing how the the inside of the atom was figured out
– JJ Thomson figures out that cathode rays are electrons, ideas of Rutherford
(small positive center), Bohr (quantized electron orbits) deBroglie
(electrons have wavelength which fit in Bohr's orbits) Schroedinger
(develops an equation for deBroglie's wave but doesn't know what it means),
Born (suggests Schroedinger's wave equation gives probability), Heisenberg
(ties it all together with his 'uncertainty' principle) A neat wrap
up would be show the class how the Heisenberg Uncertainty Principle allows
the velocity of electrons in atoms to be almost trivially calculated.
Very early in the 20th century the structure of the atom was figured out. There were two key experiments. (what's the other?)
Rutherford's alpha recoil experiment
A few milligrams
of radium (to be precise, its decay product radon 222) was put in a lead
box with a small hole in its side. Radium decays by emitting alpha particles,
which are two protons and two neutrons (same as the nucleus of helium).
This is a heavy particle with a positive charge, and it flys out very fast,
about 1/20th the speed of light (1.5 x 10^7 m/sec). Radium is intensely
radioactive. In a one gram sample of radium-226 37 billion atoms
decay every second. This number is accurate because the number of disintegrations/sec
of 1 gram of radium-226. is used as the definition of 1 curie (1 curie
= 37 billion becquerel = 37Gbq). Most of the emitted alpha particles are
absorbed by the radium sample itself, the kinetic energy of the absorbed
particles heating the radium. Those alpha particles that are not
absorbed internally come flying off the sample in all directions. Most
hit the lead box and are absorbed, but a small fraction will exit through
the hole in the box.
The SI unit of radioactivity is the becquerel (Bq), equal to one disintegration per second. The curie is a non-SI unit defined as that amount of radioactivity which has the same disintegration rate as 1 gram of Ra-226 (3.7 x 10 ^10 disintegrations per second, or 37 GBq).
This weak stream of tiny, heavy, charged, fast moving particles coming out of the lead box was used to probe atoms of various materials. Alpha particles have very little ability to penetrate material; it is often said that alpha particles can be stopped by a sheet of paper. But if what you place in the path of the alpha particles (as a target) is thin enough most of the alpha particles will pass through. Gold foil is a good choice of target. Gold (atomic number 79) is an element that does not react chemically, so gold samples can be very pure (nearly all atoms the same), and most importantly the techniques for pounding gold into extremely thin gold foils had been known for centuries. Some targets used in the experiments were gold foils as thin as 6 x 10^-8 m, which is only about 200 atoms thick since the radium of a gold atom is 0.15 nm (dia of 3.0 x 10^-10 m. (one ref, Crooks, says the foil was platium)
Alpha particle detectors were placed all around the foil target to measure the angle of the alpha particles that exited. Alpha particles hitting a zinc sulfide screen were known to make the screen scintilate, meaning it put out a brief, dim flash of light every time a single alpha particle hit was absorbed. The alpha detectors used in the experiment were the experimentors who stared for hours in a darkened room using low power microscopes at the surounding zinc sulfide screens and counted how many light flashes occurred in each screen. The maximum number of flashes per minute that could be counted this way was about 90.
Think about it, this is pretty remarkable. A visible flash of light results from the kinetic energy stored in a tiny piece of the nucleus of a single atom being absorbed by a zinc sulfide crystal. In fact luminous watch dials for many years were made by mixing a tiny amount of radium with zinc sulfide. The radium concentration for watch dials was set to produce about 200,000 flashes per second. When looked at under a glass in the dark the glow could be seen to be composed of a huge number of tiny light flashes.
London, 1903 --- (as the story goes) Sir William Crookes was entertaining himself by observing the fluorescence that alpha rays from radium produce on a zinc sulfide screen, when he spilled some of the radium. Radium at the time was rare and expensive, so to locate and recover it all he checked the screen under a microscope. And what he saw astonished him! Rather than the expected uniform glow, he observed discrete flashes of light - each flash produced by an individual alpha particle!What was found was that most of the alpha particles went through the target with little or no deflection in angle. However, a few (1 in 8,000) were deflected at high angles (> 90 degrees) with some even bouncing back toward the emitting box. One inescapable conclusion was that most of an atom must be relatively empty (no mass or charge concentration) allowing most of the alpha particles to sail right through. A further conclusion was that the most likely cause of a few alpha particles recoiling back or being deflected at high angles.must be that they hit (or came very close to) a very dense concentration of positively charged mass, now known as the nucleus. By measuring the ratio of the particles that sailed though with little to no reflection to those particles that were deflected greatly, and correcting for how many atoms thick the target was, it was possible to estimate that the ratio of the nucleus dia to the atom dia.Note for this story to be true the amount of radium he was looking at must have been really, really, tiny. The spec of thorium in my Spinthariscope has a 14 billion year lifetime, yet even under a magnifier there are so many flashes per second that the flashes blend together into a shimering glow, no individual flashes are visible.
That ratio of nucleus dia to atom dia came out to be about 1 part in 10,000 for gold, which has a big nucleus, and is about 1 part in 100,000 for elements down low on the periodic chart. A good visual image for hydrogen is this: Imagine proton as a tiny dot 1 mm in dia. Where is the electron? On average it's about 50 meters away (ratio of 100,000)! The nucleus occupies an incredibly tiny portion of the volume of an atom. (One scientist's famous image for the nucleus was a 'fly in a cathedral'.)
I found this little gem in a UCLA freshman chemistry tutorial on atom size --- "The nucleus is really, really small. How small? - We don't really care (they're chemists!). Go and ask a physicist if you really care."This experiment was done in 1909 by Geiger and Marsden who worked in Rutherford's lab. Rutherford and Geiger had run tests with the detecting screen behind the target. There were weak hints that a few alpha particles were getting lost, so they planned a test with screens at large angles. However, they were just being thorough and thought it very unlikely there were any large angular deflections so they assigned the test to undergraduate (Marsden).The Wikipedia link is here
Spinthariscope
I was surprised
to find you can buy a device that lets you see alpha particles flashes
in the same way it was done 100 years ago. It's called a spinthariscope.
I bought online a Spinthariscope from UnitedNuclear.com
($30 + shipping). Thousands of flashes per second (claims manuf) in 'activated'
zinc sulfide from thorium alpha particles. Thorium 232 has a 14 billion
yr
half life (about the age of the universe).
What do you see? I think you see flashes, but they are kind of lost in a swimming sea of dim light. If there was less thorium it might be better because individual flashes might be more easily seen. Rutherford's boys counted individual flashes. They had confirmed with the recently invented geiger counter, which responds to individual alpha particles, that each scintillation flash came from a single alpha particle. They estimated they probably counted as many as a million flashes in their experiments!
Let's estimate how many thorium atoms in the Spinthariscope
explode per second
Guess: 0.1 gram of thorium/232 gram
per mole= 4.3 x10^-4 mole
tau=1.44 x 14 billion = 20 x10^9 yr
sec/yr = 8.6 x 10^4 sec/day x 0.365
x10^3 day/yr = 3.1 x10^7 sec/yr
# of atoms = 4.3 x 10^-4 mole x 6
x10^23 atoms/mole = 26 x10^19 atoms = 2.6 x10^20 atoms
probability of an atom decaying in
one sec=1/tau in sec = 1/(20 x 10^9 yr x 3.1 x 10^7 sec/yr)
= 1/(62 x 10^16 sec) = .016 x 10^-16 = 1.6 x 10^-18
# of disintegrations/sec = 1.6 x 10^-18
probability x 2.6 x10^20 atoms
= 420 disintegrations/sec (0.1 gram)
This is order of magnitude agreement with what it looks like and with the manuf's claimed flash rate.


Alpha particle ( Wikipekia)
Alpha particles
are emitted by radioactive nuclei such as uranium or radium in a process
known as alpha decay. This sometimes leaves the nucleus in an excited state,
with the emission of a gamma ray removing the excess energy. In contrast
to beta decay, alpha decay is mediated by the strong nuclear force. Classically,
alpha particles do not have enough energy to escape the potential of the
nucleus. However, the quantum tunnelling effect allows them to escape.
When an alpha particle is emitted, the atomic mass of an element goes down by roughly 4 amu, due to the loss of 4 nucleons. The atomic number of the atom goes down by 2, as the atom loses 2 protons, becoming a new element. An example of this is when radium becomes radon gas due to alpha decay.
The energy of alpha particles emitted by radium during nuclear decay have energies of about 5 MeV, more precisely 4.871 MeV energy released per disintegration. This is a lot of energy. For reference the first proton particle accelerator, which was build in Rutherford's lab, accelerated protons through only a few hundred thousand volts. Another reference point is that 5 MeV is energy released when two deuterium nuclei fuse to form a helium nucleus. I suspect the energy of alpha particles from radium is so high because the alpha particle, once it tunnels out of the nucleus, finds itself in a very strong electric field (pointing outward) created by the remaining 86 protons in the nucleus.
Alphas particles travel only a few centimeters in air producing about 5,000 ion pairs per mm. When they stop moving, they grab two electrons and become an atom of helium. Because of their charge and large mass, alpha particles are easily absorbed by materials, and they can be absorbed by tissue paper or the outer layers of human skin (about 40 micrometres, equivalent to a few cells deep) and so are not generally dangerous to life unless the source is ingested or inhaled.
Alpha emission and
recoil
The
decay of radium 226 with emission of an alpha particle releases 4.871 Mev
of energy. Most, but not all, of this energy goes into the alpha particle.
We can use conservation of momentum to figure how the energy divides between
the emitted alpha particle and the recoiling nucleus:
m x v (radon nucleus) = m x v (alpha particle)
The radon nucleus is roughly 50 times heavier than the alpha particle (to be exact 55.5 = radon 222/alpha 4). So the emission of the alpha particle causes the nucleus to 'recoil' with about 2% of the velocity of the alpha particle. In terms of energy (1/2 x m x v squared) the nucleus compared to the alpha has 1/50th of the velocity and x50 mass so it has about 2% of the energy of the alpha particle.
The recoil of the nucleus is an energetic event. Since the alpha particle comes out at about 1/20 the speed of light, the nucleus takes off at 1/1000 the speed of light, which is 3 x 10^5 m/sec with an energy of about 100 kev (=2% x 5 Mev). It can move quite a ways. Here is an animation of the disruption in a crystal due to a much lower energy recoil of 1 kev.
http://www.esc.cam.ac.uk/movies/zir600.html
The link below is a lecuture by a chemistry prof at UCLA. He discusses how boron-10 easily captures a thermal neutron to form an 'excited' boron-11, and its decay has the potential to be useful as a killer of cancer cells. Surprisingly (to me) even though boron-11 exists naturally and is stable, the newly created 'excited' boron 11 is unstable and decays thowing off an alpha particle. Energy output is 2.4 Mev. He describes the alpha particle and recoiling lithium nucleus as ions and says they travel about one human body cell diameter (25 microns) and "the ions produced from the fission reaction are energetic and heavy on an atomic scale and they plow through the cell (creating an ionization trail) and virtually tear the cell to pieces." However, he says, to be sure and kill a cancer cell you want about 100 boron atoms attached to it.
http://web.chem.ucla.edu/~mfh/
Beta particle energy
It took a long time to understand the mechanism of beta decay. In the early
years energy of charged particles was measured by running the particle
through a magnetic field (causing them to bend) and onto photographic film.
Above I calculated that bending varies inversely with particle mass x velocity
(momentum), so low energy particles bend the most.
sideways travel = 1/2 x k x charge x B/(mass x vel)
Do the relativistic speeds of beta particles complicate the bending response? Maybe. Special relativity shows that as the speed of light (c) is approached and velocity begins to flatten out, then mass (effectively) begins to increase. So the denominator of my (approx) bending equation increases with particle energy at low speeds due to increases in vel and near c due to increases in relativistic mass. However, vel goes up as the square root of energy (E = 1/2 m c^2), whereas the general formula for relativistic mass is mass = energy/c^2 (Wikipedia). Hence there may be a complication as sideways travel transitions being (approx) inversely proportional to the square root of energy to being inversely proportional to energy up near c. (I read that the concept of relativistic mass is tricky to use. For example, F=Ma is not correct with relativistic mass, so my bending equation, which was derived from F=ma, may very well not apply at relativistic speeds.)A bending energy test done with alpha particles yielded (I presume) a nice sharp line, showing that all the alpha particles (for a particular element/isotope) have the same energy. When done with beta particles though, the result was messy. Some elements showed a continuous background with a few bright lines. Others had only weak lines, and some had no lines at all just a continuous energy range. All other energies of the atom seemed to be quantized and E=m x c^2 considerations predicted a fixed energy output, so where was the missing energy? It was all very puzzling. The answer (for some decays) was found to be that the decay was producing both beta particles and gamma rays, but most beta decays continued to puzzle.
The tendency at the time was to focus on the energy peaks (bright lines) in the beta energy data and ignore the background. This seemed reasonable, because in cases where the spectrum was a mixture of continuous and peaks, like the sun's spectrum and Moseley's 1913 element x-ray spectrum, it was the frequency of the peaks that provided useful atomic data.
It (much) later came to be understood that the beta energy peaks were a secondary phenomena. Gamma rays (with fixed energy) coming from the nucleus decay were sometimes absorbed by outer electrons of the atom and ejected. These were the beta particles that formed the peaks, their energy reflecting the energy of the gamma rays. The beta particles (electrons) directly ejected from the nucleus have a true continuous spectrum.It took better instrumentation to properly measure the continuous nature of the beta spectrum. In 1914 Chadwick (the first to observe the neutron) made much better measurements of beta energy using ionization equipment designed by Hans Geiger, thus confirming that beta energy spectrum was indeed truly continuous.
After years of no progress in understanding beta energy, Wolfgang Pauli in 1930 suggested weakly (in a letter, he said he dare not publish this crazy idea) that maybe another, unseen, particle was coming out (carrying the missing energy), and he took a stab at estimating its properties. Enrico Fermi started calling the mystery particle the 'little neutral one' or neutrino. Later in the 1930's Fermi, based on his experimental and theoretical work, produced a complete theory of beta decay. The neutrino was not found experimentally until 1956.
Thus the solution to the 'missing mass' problem in beta decay was found to be that the atom was emitting an unseen particle, called the neutrino (or anti-neutrino), which carried off the missing energy. Neutrino's are often called 'ghostly' particles. They interact with normal matter so weakly that most will pass through the earth without being stopped, and billions of them pass through your body every day without being noticed or doing any harm.
Positron Emission Tomography (PET scans)
Proof that
anti-matter exists is that positrons (anti-electrons) are routinely used
in Positron Emission Tomography to make brain scans. This is done by injecting
into the patient biologically active molecules (like a sugar) tagged with
positron emitting atoms.
The atoms commonly used are isotopes of atomic numbers 6 to 9 that are a little too light to be stable, i.e. they are one neutron short of a stable state: carbon-11 (20 min), nitrogen-13 (10 min), oxygen-15 (2 min), or fluorine-18 (110 min). Typically they are made by firing protons (in a cyclotron) at elements in this atomic range. (Only fluorine with it roughly two hour decay time lasts long enough to be shipped to remote scanning sites.) A captured proton will raise the atomic number by one, but now the element is unstable because it does not enough neutrons at the higher atomic number, so it decays by firing out an anti-electron (positron) plus a neutrino that removes a positive charge and lowers the atomic number by one. Position emission can only occur when the decay energy (due to mass loss) exceeds 1.022 mev, which is twice the rest mass energy of an electron. The positron travels a few mm (so says Wikipedia!!) in the body before annihilating with an electron.
The key that make Positron Emission Tomography work is that the positon/electron annihilation produces a pair of gamma rays each with energy 0.511 mev (rest mass energy of electron) that travel in 180 degree opposite directions. Why 0.511 mev? This is a 'low energy' annihilation, meaning the kinetic energy of the particles is low compared to the rest mass energy. The reason for a gamma ray pair at 180 degree (nominal) is conservation of momentum. The PET scanner only registers (via scintillation) gamma ray pairs that arrive nominally simultaneously. This forms a line from which the photons could have been omitted, and newer PET scanner can localize along the line by using picosec detectors and measuring time of flight. Obviously to make a scan of the brain a significant number of the 0.511 mev gamma rays must be able to penetrate a significant distance in brain tissue and escape to the detectors in the machine.
Geiger counter
Alpha and beta particles
(as well as high speed protons and some gamma rays) when they pass through
matter cause direct ionization, meaning that they transfer some of their
energy to the electrons of the atoms they zip through, ripping the electrons
free of the atoms and leaving them free to move about. Air that is 'ionized'
is briefly changed from an insulator to a conductor (along the particle
path).
The geiger counter was invented in 1908 by Hans Geiger (one of Rutherford's boys) to count alpha particles. A geiger counter has a gas tube with voltage across the gas. When an ionizing particle zips through the gas it leaves in its wake a transient conducting path. The voltage between the electrodes in the tube causes the (transiently) free electrons in the gas to flow, forming a current pulse that is detected and counted. In this way a geiger counter can count individual ionizing particles.
However, even after the invention of the geiger counter, Rutherford in many experiments, like the famous alpha recoil experiments, detected alpha particles visually (in the dark) from scintillations (light flashes) they cause in some materials. The geiger counter was used to confirm that
one scintillation flash ?==> one alpha particle
Individual alpha particles could (in effect) be seen.
Detecting neutrons
Moseley's
had shown in 1913 (using element x-ray emissions) that elements should
be ordered by atomic number not atomic weight. It was known at the time
that almost all the mass of the atom was in the nucleus. Atomic weights,
especially in lower elements on the periodic chart, tended to be (nearly)
simple integers, so it was pretty clear from 1913 on that there must be
a neutral particle in the nucleus to supply the missing mass, and
it must weight about the same as a proton.
hydrogen atomic
number 1 atomic weight
1.01
helium
atomic number 2 atomic weight
4.00
lithium
atomic number 3 atomic weight
6.94
beryllium
atomic number 4 atomic weight
9.01
boron
atomic number 5 atomic weight
10.81
carbon
atomic number 6 atomic weight
12.01
A complicating factor, though (there's always a complication!), was that measured atomic weights (obtained by chemists from weight ratios in chemical reaction) reflected a weighted average of naturally occurring isotopes, which at the time were (largely) unknown. The deviation from simple integer values is seen above most clearly above in lithium and boron.So even though people were pretty sure neutrons were probably 'in there', it was almost 20 years (1913 to 1932) before neutrons were detected.
The man problem in looking for neutrons was that ionization detectors (geiger counters) couldn't be used. A neutron, having no charge, does not interact strongly with electrons as it zips thorough atoms, so it doesn't leave a trail of free electrons behind it. It was later found that ionization detectors, while they couldn't detect neutrons directly, could be used to detect them indirectly. It was found that if a thin layer of hydrogen containing material was placed in a (supposed) neutron beam, ionization detectors would be detect particles behind the material. The interpretation was that neutrons, which have about the same mass as protons, were occasionally hitting them and knocking them out. The maximum energy of the knocked out protons provided information on the energy of the incoming neutrons.
Chadwick's neutron
generator
Chadwick won
the 1935 Nobel phsics prize for the discovery of the neutron. Chadwick
apparatus for generating a stream of neutrons was remarkably simple. Inside
a vacuum chamber he placed vertically a 1 cm disk painted with a polonium
(atomic number 84), which was known to be a strong alpha emitter, 5,000
times higher than radium, and right next to it he placed a slightly larger
(2 cm) disk of pure beryllium (atomic number 4). The presumed neutrons
coming off the beryllium then exited through a window in the vacuum chamber,
passed through a few inches of air where varius materials were placed during
experiments, and then into an ionization chamber whose current pulses were
measured and photographed with an early oscilloscope.
When there was no material in the gap the ionization chamber output was low. Neutrons having no charge do not ionize the gas in the chamber. When a material rich in hydrogen, like parafin, was put in the gap the ionization chamber gave a strong output. The interpretation was that neutrons were hitting the hydrogen nucleus (protons) in the parafin and kicking them out. It was the charged protons going through the ionization chamber that were being detected. From the shape of the current pulse they knew they were detecting protons. The energy of the protons was figured by inserting various thicknesses of blocking material in front of the chamber. The protons were found to be coming in as fast as 10% of the speed of light, so that told them that the neutrons had to be coming out of the beryllim at 10% of the speed of light.
The transfer of energy from the neutrons to the protons in the targets in the gap was physical, like two billiard balls hitting. But the reaction in the beryllium was different, this was a nuclear reaction. When an alpha particle from the polonium was absorbed into the beryllium (atomic number 4) nucleus, it created unstable carbon, and as it decayed it converted some of its mass to energy which was shared by the exiting neutron and newly created recoiling carbon ion. The references give the equation below.5 Mev alpha particles travel at about 5% the speed of light. If most of that energy is transferred to a neutron (or proton) with 1/4th the mass, it will travel near 10% the speed of light..
Be9 + alpha => C12 + n (5.7 Mev neutron)
I've noticed something peculiar about this reaction. Presumably when the alpha particle merges with Be9 (element 4), it briefly forms an (excited) C13 (element 6), which then decays to C12. But C13 is a stable isotope of carbon! The only thing I can figure is that C13 throws out a 5 Mev neutron because it's born in a highly excited and needs to shed energy.Tom Leher's song 'Elements'
Polinium-210
Polonium-210's
short 138 day half life makes it incredibly radioactive, about 5,000 more
radioactive than radium. According to Widipedia 1 mg of polonium puts out
as many alpha particles (5.4 Mev) as 5 grams of radium. The ratio of alpha
output should be (about) the ratio of half lives, let's check. Radium 226
half life is 1,602 years or 585,131 days. So ratio is 5.85 x 10^5/1.38
x 10^2 = 4.24 x 10^3 (4,240), close enough. 1 gram of polonium puts out
140 watts of heat! Air near polonium is so ionized that it glows blue.
Riff on ingestion of Polonium 210 --- In Nov 2006 a former Russian spy in England was poisoned with polonium 210 and over several weeks died from the internal alpha radiation damage. A curie is the amount of radiation given off by 1 gram or radium in one second. The lethal does of alpha radiation if ingested is estimated to be 3 to 10 millecuries. A guest editorial in the Wall Street Journal claimed 10 millecuries of polonium was 0.2 micrograms, about the size of a few grains of salt. I saw a TV reporter claim the spy was buried in a lead lined casket because his body was so radioactive (idiots)!Here is a link to a 1932 Chadwick paper where he describes his apparatus and the various experiments that allowed many of the properties of the neutron to be deduced.Doing the math --- (density of polonium and radium are within a factor of 2, so here I just assume them to be the same) 10 millecuries would be 10^-2 gram of radium. Since polonium is 5,000 times as strong an emitter it would weight (about) 5,000 less, which is 0.2 x 10-5 gram or 2 microgram, not 0.2 microgram as it says in the editorial. I checked out salt grains and they are really, really tiny. Squarish grains of salt from my salt shaker measure about 0.33 mm on a side, so that's 27 grains per cubic mm. Density of polonium is 9.1 x 10^-3 gram per cubic mm (9,100 micrograms). So a salt grain size particle of polonium 210 would weigh 1/27 x 9,100 micrograms = 337 micrograms. Thus a 2 microgram lethal dose is less than 1% the volume of one grain of salt!! Yikes. A dose the size of a few salt grains would weight about 1,000 micrograms and would output 5 curies of alpha radiation! This is x500 times the estimated 10 millecurie lethal dose.
Polonium is a fairly common industrial isotope used to ionize air to eliminate static electricity from fast moving rolls of textiles, film, or paper. There is little regulatory control of polonium alpha sources below the two curie level. Almost all (97%) commercial polonium is made at one reactor in Russia by irradiating bismouth 209. In one year they make about 3 ounces (85 grams).
Fermi uses neutron generator to activate elements
A year or
so later Fermi built a beryllium neutron generator similar to Chadwicks
except the alpha particles used to irradiate the beryllium came not from
polonium but from radon gas harvested regularly (radon's half life is only
about four days) from a sample of radium. Fermi used the neutrons to systematically
neutron irradiated nearly every element to activate it. What he
did was put various elements in the path of the neutrons, and if they became
radioactive use the ionization chamber to measure the decay profile. He
could sometimes identify several different decay rates in the data, and
this was evidence of the existence of different isotopes of this element.
Initially he found most elements did not become radioactive when irradiated with the neutrons from his source. The neutrons hitting his targets from the beryllium were mostly moving very fast, as fast as 10% of the speed of light. It turns out that that neurons moving this fast are not readily absorbed by the nucleus of most elements. One day Fermi tried putting some paraffin (made of hydrogen and carbon) between the source and the target, and he was amazed to see he got much more response from his ionization tube. He had made one of his most important discoveries of his life. He had found a material now called a moderator. This is a material that allows the neutrons to bounce around inside without absorbing them, slowing them way down to what are called thermal neutrons. Slow thermal neutrons are much more easily absorbed by the nucleus of materials. Fermi repeated his experiments irradiating every element he could get his hands on with slow neutrons.
It is now known that virtually every element can exist, at least briefly, with different numbers of neutrons, that is, it has (many) different isotopes. Even the simplest atom hydrogen has an isotope with one neutron, deuterium, and a radioactive isotope with two neutrons, tritium. Some elements have dozens of isotopes, nearly all of them radioactive.
A moderator turned out to be an essential component in the design of nuclear reactors. A moderator material is need to slow down the fast neutrons from the uranium-235 fission to allow them to be absorbed by more uranium-235 to keep the reaction going. During world war II it was Fermi who designed and built the world's first nuclear reactor. Here is a lecture on Fermi's early experiments with neutrons.
http://www.osti.gov/accomplishments/marburger.html
First nuclear fission
TV version
--- In a recent PBS 2 hour show (E=m x c^2) Meitner
and Frisch on a snow hike in Sweden are discussing the puzzling results
of Hahn and Strassmann's experiments at Meitner's old lab in Berlin. Hahn
and Strassmann were building on Ferimi's and Joliot-Curie's work shooting
neutrons at uranium trying to create new, higher atomic number elements
via beta decay. Strassmann thinks he is seeing two isotopes of the relatively
light element barium (from decay rates and other analytical measurements)
in the samples which he and Hahn can't explain because they are expecting
elements heavier than uranium.
In the show Firsch says to Meitner that if uranium did split in half the repulsion of the two charged halves of the split nucleus would require 200 Mev of energy. {This is a high energy, an order of magnitude larger than any nuclear reaction seen. Alpha particle energy from radium is about 5 Mev} Meitner, who long worked with Hahn, then checks the 'packing factor's (for barium ? uranium?) saying that mass (supposedly of two low end barium isotopes vs uranium) is lower by 1/5 of a proton. Using E=m x c^2 she finds the missing 1/5 proton mass provides just the needed 200 Mev energy. In the show there is then a dramatic pause, then Frisch, who is Meitner nephew, says she has just discovered nuclear fission.
Check -- 1/5 x rest mass of protonShe showed that presence of barium could be explained quantitatively if the uranium nucleus was spitting. Since Haln and Strassmann were finding barium in their irradiated uranium samples, most likely the firing of neutrons into the uranium was causing its nucleus to split. The dynamic model at the nucleus widely used at that time was that a large nucleus was like a large, unstable, water drop which can if disturbed split in two.
= 1/5 x 1,000 Mev (approx) = 200 Mev (approx)What Meitner and Frish did was to make sense of someone else's data (Hahn and Strassman)! Well, that's (more) than a little unfair, because Hahn, a chemist who was her long time collaborator, had written to Meitner asking her if she could make sense of his recent results. And, furthermore, the only reason she was not with Hahn in Berlin is that she was a jew and had been recently forced out by the Nazis.
Cropper's version --- A more nuanced, and probably more accurate, version of the first fission is given in the book Great Physicists by William Cropper. Strassman was sure he was seeing barium, so he was prepared to claim uranium was fissioning, although he couldn't explain how. Hahn was more cautious and wrote to Meitner asking if she could interpret the data. She wrote back saying she didn't see how uranium could be fissioning.
A little later her nephew Frisch, who is a physist working with Bohr in Copenhagen, comes to visit her in Sweden. On a snow walk they discuss the matter, then sit on a log and both start calculating on scraps of paper. Bohr had a theory the nucleus was like a drop of liquid with surface tension, and it could wobble. The calculation was this: if the nucleus 'wobble' caused an elongation and thinning of the center, was the charge repulsion of the two ends high enough to overcome the 'surface tension'. Their calculation out on the snow finds that the repulsion is just about large enough to overcome the surface tension. As in the TV version Meitner remembers the masses and finds the mass loss is just enough to supply the 200 Mev kinetic energy the halfs acquire as their positive charges push them apart.
Frisch goes back to Copenhagen and tells Bohr about it. Bohr accepts the theory immediately, slapping his forehead and saying "Oh, what fools we have all been" and within hours sails for US. Frisch spends two days doing a confirming test (detecting the energetic fission fragments). Frisch and Meitner write up their theory, and Frisch writes up his test, and the two papers are sent to the journal Nature.
On the ship Bohr discussed the theory and data with Rosenfeld. They are both convinced fission is happening, and are sure it is an important result. Bohr (supposedly) forgets to tell Rosenfeld to keep quiet about it until Frisch and Meitner can publish. Rosenfeld on landing in US goes to Princeton and tells a physics seminar audience "all about nuclear fission", and Cropper adds, "The news created a sensation." Everyone rushed to the lab to confirm Frisch's test, and it was soon confirmed by Columbia and by Joliot in Paris.
Frisch's fission confirming experiment
I have found
two references that say Frisch did a cloud chamber test. But I don't see
anything about a cloud chamber in his paper???
In just two days with only a little lab equipment Frisch confirmed (in a test suggested by Placzek) that neutrons could split uranium atoms. How did he do it? Well, there were three steps: He built a neutron source, he got the neutrons to bombard uranium, and, most importantly, he confirmed that (a few) uranium atoms were split. But how? He couldn't do a chemical separation, because there was not enough material. The key was to exploit the huge 'recoil' energy (200 Mev) the fission fragments would have.
To make a neutron source he did what Chadwick did a few years earlier. (See my section in this essay on Chadwick's neutron generator.) He mixed radium (300 mg) with beryllium. The alphas from the radium eject neutrons from the beryllium. He calculated that the uranium fragments, which have a large charge of 20 or so, would be incredibly ionizing, and could travel only a few mm in air before they lost all their energy tearing electrons out of air molecules. The radium/beryllium mixture was made into a thin layer and placed close to a layer of uranium. He had (or built) an electronic device to pick up the air ionization (essentially a geiger counter), and he could display the current picked up by his ionization detector on an early oscilloscope.
When he adjusted the threshold of his ionization detector high and counted, he picked up trips (few a minute) only when the radium/beryllium was put near the uranium. When he set the threshold low and displayed its output on the oscilloscope, the occasional large ionization pulse (from a uranium split) could be seen mixed in with many much smaller ionization pulses (from the radium alphas).
Early published fission references
Here's a link
to Frisch's and Meitner's brief letter on uranium fission, which appeared
in Nature on Feb 11, 1939. Two weeks later Nature published Frisch's brief
letter on his confirming experiment and a letter from Bohr appeared, saying
he wanted comment, "Due to the extreme importance of this discovery".
http://dbhs.wvusd.k12.ca.us/webdocs/Chem-History/Meitner-Fission-1939.html
http://dbhs.wvusd.k12.ca.us/webdocs/Chem-History/Frisch-Fission-1939.html
http://dbhs.wvusd.k12.ca.us/webdocs/Chem-History/Bohr-Fission-1939.html
Reading Frisch's and Meitner's famous fission letter I am amazed at how little it says. First they point out that Hahn has already published that he is quite sure barium is being created when uranium is irradiated, so the experimental evidence is already in that neutrons split uranium. (Hahn wins the 1944 Nobel prize for chemistry for this. Note this is a German being awarded the prize during the 2nd world war!) The only 'explanation' in the letter as to how it splits is they say, 'well it's like Bohr's classical liquid drop/surface tension sort of thing (not tunneling), and (hey guys) you've got to remember that the (effective) surface tension is of this drop lowered because this this drop is charged. Basically that's it.A few months later (Sept 1939) Bohr and Wheeler (from Princeton) together publish a paper showing that the only uranium isotope with a high likelihood of fissioning was uranium 235 (only 0.7% of natural uranium) when hit with slow neutrons. Leo Szilard objected to this paper being published (on security grounds), and soon thereafter all work on uranium fission was classified.While Meitner and Frisch don't say this, the message (I think) is that if you think of a wobbly large drop that is charged, you will see that if happens to neck down a little in the center the opposing charges of the two sides will push apart against the surface tension (effectively lower the tension), hence it can split into two drops easier than if it was not charged. No wonder Bohr, who was the developer of the liquid drop nuclear theory, slapped his head and yelled, of course, when Frisch first mentioned the idea it to him.
Bohr in his follow up comment letter two week later says, (Yup, fission can indeed be explained as) "stressed by Meitner and Frisch, mutual repulsion between the the electric charges in a nucleus will for highly charged nuclei counteract to a large extent the effect of the short-range forces between the nuclear particles in opposing a deformation of the nucleus."
---------------------------------------------------
Fast or slow neutrons?
Uranium 235
fissions readily with slow neutrons. U235 even in natural uranium can support
a sustained chain reaction as long as a moderator (like graphite) is used
to slow the neutrons from the uranium fission. In fact this is how Fermi
first atomic pile worked. Uranium 238 (99.3%) can fission too, but only
if hit by fast (> 1 Mev) neutrons. Bombs are sometime jacketed with u238
to increase the fission yield. U238 will not, however, support a chain
reaction.
The neutron source of the 1930's used by investigators was beryllium irradiated by high energy (5 Mev) alpha particles from radium (or radon), so this type of neutron source put out fast (high energy) neutrons. Fermi had discovered as early as 1934 that slowing neutrons, by passing the neutron beam through a light material like paraffin or water, greatly increased (factor of 100) the effect of the neutrons had on many elements including uranium. The explanation was the slow neutrons did not zip by the nucleus so fast and were much more readily absorbed than fast neutrons. (The quantum mechanical explanation is that the slower neutrons had longer wavelength that 'fit' better with the size of the nucleus.)
I wondered if Frisch and Hahn ? Strassmann used moderators in their neutron irradiation of uranium. I have been unable to find any references about this. My guess is that Hahn ? Strassmann were moderating to get slow neutrons, because they needed a lot of reaction product to do chemical separations. This would mean that their reaction products came almost entirely from u235 disintegrations, but of course, they didn't now this because the large cross section of U235 to slow neutrons was not figured out (by Bohr) until a little after their experiments.
Frisch's brief
description of his confirming experiment does not mention a moderator.
At first this bothered me, but I now think his experiment would work with
out a moderator. Neutrons direct from his beryllium source probably had
enough energy (> 1 Mev) to cause u238 to ionize. He didn't need a lot of
reaction product because he was detecting individual ionization events
with his electronics. If he didn't use a moderator and Hahn ? Strassmann
did, then his test was not quite as confirming as he thought, but in the
long run it didn't matter.
----------------------------------------------------
Fermi's systematically irradiated many different elements starting first
with fast neutrons (neutrons direct from is radon/beryllim source). One
day in 1934 he tried putting paraffin between his neutron source and target
and was amazed to find that his targets could become x100 times more radioactivity.
The paraffin was acting as a moderator, slowing down neutrons as they bounced
off hydrogen nuclei, which have about the same mass as neutrons.
---------------------------------------------------
In biographical material on Placzek he is quoted as asking Bohr in early 1939, 'Why it is that slow neutrons spit uranium and not fast neutrons.' Bohr doesn't know, but (so the stories goes) Bohr runs off to his office and in 10 minutes he has the answer. The neutron (capture) cross section of uranium is higher for slow neutrons than fast, because the slow neutrons are being captured by u235.-- Fermi took radon from the disintegration of a radium source and mixed it with beryllium powder and sealed it in a glass tube.
-- The results
were astonishing—parffin increased the silver's radioactivity increased
a hundredfold.
---------------------------------------------------
'Race to build bomb' lecture
Here's a link
to a 46 page lecture on people and experiments from discovery of radioactivity
to the fission bomb. I've only scanned it, but it looks like it has two
real strengths: tons of good pictures and excellent color science sketches.
http://web.umr.edu/~rogersda/american?military_history/AtomBombLectureNotes.pdf
Barium
Barium is element 56. Wikipedia list 39 isotopes of barium, seven of which are stable. All the stable isotopes of barium are found in nature at quantities above 0.1%! A barrium isotope exists for every atomic weight from 114 (58 neutrons) to 153 (97 neutrons). Isotopes 130 and 132 are stable and isotopes 134 through 138 are all stable. Because 72% of barium is isotope 138, the atomic weight of the element barium is listed as 137.327, just a little less than the weight of the dominant isotope.Half the weight of the dominant isotope of uranium 238 is 119, and half of the minor, less stable uranium isotope 235 is 117-118. So an (almost) exact split of uranium could indeed produce (two) radioactive isotopes of barium, because the weight range for barium extends down to 114. A check barium half lifes show most of the light isotopes have half lifes from a sec or so to a few minutes that would make them measurable with the technology in the 30's.
Hahn and Strassman's paper
Otto Hahn
and Fritz Strassman in a follow up Feb 1939 paper report detecting three
isotopes of barrium. They describe their neutron source as a "radium-beryllium"
generator. They irradiated 15 grams of uranium for 12 hours, and say "2
g of barium in the form of its chloride were precipitated from the solution
containing the irradiated uranium".
What! 2 grams of barium from 15 grams of uranium in 12 hours? How is this possible from the weak neutron stream from a radium-beryllium generator, unless a weak chain reaction occured! Maybe a translatation problem (paper was in german)?
Hahn ? Strassman
closest modern lifetimes
-----------------------
-----------------------------
14 +/- 2 min beta decay
barrium 124 11.0 min
barrium-127 12.7 min
86 +/- 6 min beta decay
barrium-126 100 min
250-300 hour beta decay
barrium-131 11.5 days
http://dbhs.wvusd.k12.ca.us/webdocs/Chem-History/Hahn-fission-1939b/Hahn-fission-1939b.html
(from) Excellent reference on fission
http://www.world-nuclear.org/education/phys.htm
Slow, or thermal) neutrons are able to cause fission only in those isotopes of uranium and plutonium whose nuclei contain odd numbers of neutrons (e.g. U-233, U-235, and Pu-239). Uranium has 92 protons.
The fission and other cross sections increase greatly as the neutron velocity reduces. Hence in nuclei with an odd-number of neutrons, such as U-235, the fission cross-section becomes very large at thermal energies.
About 85% of the energy released is initially the kinetic energy of the fission fragments. However, in solid fuel they can only travel a microscopic distance, so their energy becomes converted into heat.
The longest delayed neutron group has a half-life of about 56 seconds. The delayed neutron release is the crucial factor enabling a chain reacting system (or reactor) to be controllable and to be able to be held precisely critical.
. The fission
reaction in U-235 produces fission products such as Ba, Kr, Sr, Cs, I and
Xe with atomic masses distributed around 95 and 135. Examples
U-235 + n
===> Ba-144 + Kr-90 + 2n + energy
U-235 + n
===> Ba-141 + Kr-92 + 3n + 170 MeV
U-235 + n
===> Zr-94 + Te-139 + 3n + 197 MeV
The total energy released in fission varies with the precise break up, but averages about 200 MeV* for U-235 or 3.2 x 10-11 joule. That from Pu-239 is about 210 MeV* per fission. (This contrasts with 4 eV or 6.5 x 10-19 J per molecule of carbon dioxide released in the combustion of carbon in fossil fuels.)
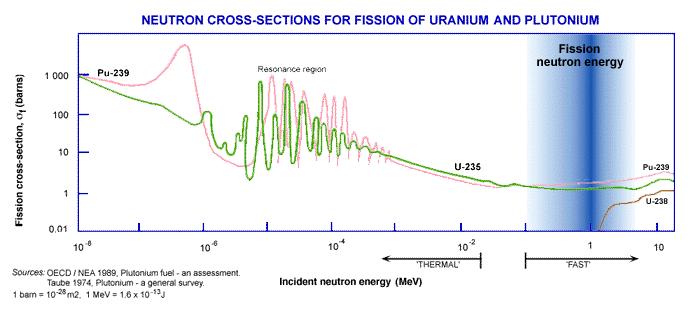
'Seeing' alpha
particles
There
are some remarkably simple, low tech ways to see (sort of) individual alpha
particles. Of course, what is really seen is the effect on other atoms
of a high speed, heavy, charged alpha particle zipping through their electrons
clouds. As the alpha particle slows down it leaves a long string of excited,
slighlty warmed, atoms in its wake.
The first method found to see alpha particles was to use zinc sulfide. Zinc sulfide emits a feint light flash that is visible to the naked eye in a very dark room when hit by a single alpha particle. Zinc sulfide emits light due to phosphorescence. Materials that exhibit phosphorescence absorb and for a while (typ msec) trap energy into their electrons spins, and then over time release it by emitting photons of a particular wavelength as they drop back to the ground state. It's a complicated quantum mechanical effect. Here is a Wikipedia link on phosphorescence
http://en.wikipedia.org/wiki/Phosphorescence
Zinc sulfide mixed with a few ppm of silver is used as the blue phosphor in TV tubes. It this application it is activated by electrons fired from the neck of the tube.
Later the Wilson cloud chamber allowed the path of the alpha particle to be seen. A cloud chamber is small box filled with super saturated water vapor, or super saturated alcohol. Passage of an alpha particle, or other charged particles, through the gas leaves a visible trail of condensation. A souped up version of the cloud chamber, the liquid hydrogen bubble chamber, was used extensively with early atom smasher machines to detect the many particles that flew out.
If a cloud
or bubble chamber is placed between the poles of a strong magnet, a lot
of information about a particle can be obtained from its path through the
chamber. The force from the magnet on a moving charged particle is perpendicular
to the instantaneous velocity of the particle because the force is a vector
cross product of velocity and B field {F =q(v x B)}. Where there is lots
of room and energy, like in outer space, charged particles will spiral
around the lines of magnetism.
When the particle passes through the liquid, it is warmed to boiling point along the track it leaves. In the wake are a trail of bubbles that can be photographed whilst still very small. The photographs are able, in this way, to reproduce accurately the path of the particle.Since the curve of the path in a chamber is a function of the particle's charge, mass, and speed, it provides information about all of these parameters. Positive particles curve one way, negative particles the other. The higher the charge and the less the mass the more the path curves. A break in a path can, if the speed is known, be used to figure the lifetime of particle.The new particles are normally produced with the help of the great, new accelerators which cause the particles to move at very great speed. This has the advantage that, although the life-span of the particle might be as little as a ten-thousandth part of a millionth of a second, the track acquires a length of several centimetres. (Luis Alvarez, 1968 Nobel Prize in Physics speech, for liquid hydrogen bubble chamber)
Radon health hazard
The large
recoil motion of the radon nucleus allows quite a few radon atoms created
by decay of tiny amounts of radium in the soil to escape the soil
into the air. Radon gas, even with its short 3.8 day half life, is in some
areas a health hazard because it is able to leak into the air in houses
and from there get into peoples' lungs. The cancer risk to lung tissue
come from the resulting three alpha decays of each radon atom in
or near the lung tissue: radon 222 down to polonium 218, then polonium
218 down to lead 214, then after bopping up through bismuth to polonium
214 via two beta decays, polonium 214 down to lead 210.
Radiation in the
human body
Every second about 7,000 naturally occurring radioactive atoms in your
body explode.
| Radioactive
Isotope |
Half Life
(years) |
Decay | Mev | Isotope Mass
in the Body (grams) |
ratio |
Element Mass
in the Body (grams) |
Activity within
the Body (Disintegrations/sec) |
| Potassium-40 #19 | 1.25
billion |
beta (89%) | 1.3 | 1.7
x 10-2 |
x 10-4 |
140 | 4,470 |
|
#6 |
|
|
|
x 10^-8 |
|
|
|
|
#37 |
|
|
0.28 |
|
|
|
|
Potassium is an essential body element and 0.012% (about 1 in 8,000 atoms) of potassium is radioactive. One of the key ionic pumps in cell walls is the Na+/K+ pump, which pumps the sodium level in the cell down and the potassium level in the cell up. There are three naturally occuring isotopes of potassium, 93.26 % is potassium-39, 6.73 % is potassium-41, and a tiny percentage (0.012 %.) is potassium-40. Potassium-40 is radioactive with a long lifetime of 1.25 billion years. The long half-life is why potassium created in stars is still around. Potassium is an essential element in chemistry of the living cell and common in the soil too. The average adult consumes about 2.5 grams of potassium a day.
About 4,470 atoms of potassium 'explode' in your body every second. Potassium-40 decays to calcium-40 (atomic number 20) mostly (89% of time) by beta decay and less often (11% of time) to argon-40 (atomic number 18) by electron capture and gamma ray (positron) emission.
About one in every 10^12th atoms of the element carbon (atomic number 6) is radioactive. There are two naturally occuring isotopes of carbon., both stable, 99% is carbon-12 and 1% is carbon-13. Carbon-14, however, is radioactive. Although it has a relatively short half life of 5,700 years, it is around because it is continually being made by cosmic rays hitting nitrogen atoms in the upper atmosphere and transmuting them to carbon-14. Crudely speaking carbon-14 is created when a thermal neutron hits nitrogen-14 replacing a proton that is knocked out.
Although only 1 in every trillion carbon atoms is radioactive, the relatively short half life of carbon-14 combined with the fact that there is a lot of carbon in the body means that about 2,600 carbon atoms 'explode' in your body every second. Carbon-14 decays to nitrogen (atomic number 7) through beta decay.
When anything living dies it stops taking in carbon, so the ratio of carbon-14 to stable carbon begins to drift down as carbon-14 atoms decays. This forms the basis for the carbon 14 dating system, which is very useful for dating organic objects back to about 50,000 years, roughly 9 half-lifes of carbon-14.
Rubidium is a group I alkali metal directly below potassium in the periodic chart and is taken up by the body as a substitute for potassium.
Twenty or so decays/sec in the body come from lead 210, a trace radioactive isotope of lead. Lead 210 is near the end of the long decay chain from uranium 238 and is intensely radioactive with a 22 year half life. It has two rapidly decaying daughter products (Bi-210 @ 5 days and Po-210 @ 138 days), which triples the decay rate. Polonium 210 decay to stable lead-206 is via alpha dec (@ 20 decay/sec). On top of its higher energy the beta particle does not travel very far, so the energy is doposited more locally. An atom decaying via alpha decay does enough damage that it is likely to kill the cell that it is in.
Here is the Uranium 238 decay chain
http://en.wikipedia.org/wiki/Radioactive_decay#Decay_chains_and_multiple_modes
Original idea for above table from "Radioactivity of
the normal human body" at this link, however, I researched the quantities
and calculated the above values.
http://rerowland.com/BodyActivity.htm
How to figure atoms/sec exploding
The decay
curve of radioactive elements is exponential. If at [time = 0] the number
of atoms in a sample is No, then at a later time [t], then remaining number
of atoms in the sample that remain, i.e. are unexploded, is described by
this equation
N = No e ^- (t/tau)
Electrical engineers use this curve all the time as currents and voltages often decay exponentially. At [t = tau], in circuits tau is known as the 'time constant'
N/No = e^-1 = 0.368 (36.8% remain)
Rather than use the natural decay parameter (tau) of the exponential decay circuit when talking about cecay rates of elements a more natural, or so think the phyicists is adopted. This is the 'half life' or the time it takes [N/No = 0.50].But for figuring atom decay/sec rate, tau has an advantage because of a very useful property of the decay curve, which is that the area under the decay curve, equals tau. This allows a simple rectangle to replace the exponential curve when initial rates are of interest, i.e. and it shows that if the the initial decay rate (decay rate at t = 0) were to be maintained. then the time it would take for 100% of atoms in a sample to explode would be tau seconds. Let's use this approach to calculate the number of atom decays (explosions) in one gram of check this for radium 226, which we can confirm from a Wikipedia article ('Radioactive Decay Law), which also does this calcuation.N/No = e^-(0.693 tau/tau) = 0.500 (50.0% remain)
half life = 0.693 tau
Radium 226
1,620 years (half life)
2,336 years (tau) =1,620 years x (1/.693)
sec/yr
3.6 x 10^3 sec/hr x 24 hr/day x 365.25 day/yr =
31.56 x 10^6 sec/yr
So at the initial (t = 0) decay rate a sample of radium 226 would 100% decay in this number of seconds:
[100% decay time at initial rate] = 2,336 years x 31.56 x 10^6 sec/yr
= 73.7 x 10^9 sec
So to figure the number of atoms/sec that explode in one gram of radium 226 we need to just divide the number of atoms in 1 gr of radium 226, which (1/226) mol, where # of atoms in a mol is Avagardo's number (6.02 x 10^23) by the 100% decay time in seconds.
# of atoms in 1 gr radium 226 = (1/226) x 6.02 x 10^23 atom/mol
= 2.66 x 10^21 atoms in 1 gr (radium 226)
[atoms explode/sec] = (2.66 x 10^21 atoms/gm)/(73.7 x 10^9 sec 100%
time)
= 3.61 x 10^10 decays/sec-gm (radium 226)
check (Wikipedia gets 3.6 x 10^10 decays/sec)
Elements in the human body
Wikipedia
(Chemical elements of the body) says the average 70 kg adult contains approximately
6.7 x 10^27 atoms and is composed of 60 chemical elements. Since the human
body has about 10^13 cells (scaling from 1,000 cells, 1 mm long C elegan
worm), this means the average human cell is made up of 6.7 x 10^14 atoms.
Wow, 670 trillion atoms/cell!
CheckHow many atomic disintegrations/sec in your body does it take to kill you?
81% of the mass of the body is oxygen (65%) and carbon (18%), with an average molecular weight of about 15. Hydrogen is 10%. For a 70 kg 'standard' man we figure the moles and mulitply by 6 x 10^23 (Avegardo's number). Values below agree nicely with Wikedia value. Interesting that even though hydrogen is only 10% the mass of the body (mostly in water), 63% of the body's atoms are hydrogen.O & C (0.81 x70,000 grams/15 gram/mol) mol x 6 x 10^23 = 2.3 x 10^27
H (0.1 x 70,000 grams/1 gram/mol) mol x 6 x 10^23 = 4.2 x 10^27
The lethal dose of 100 million disintegrations/sec is about 10,000 times the normal explosion rate of 7,000 atms/sec. But there is another factor in the comparison. Polonium 210 is an alpha emitter whereas most of the natural atoms in your body decay by beta emission. Alpha decays are much more dangerous than beta decays because each alpha decay releases x10-20 more energy than a beta decay, and because alpha particles are less penetrating, the energy is deposited in a smaller region. One estimate is that an alpha decay is 100 times more likely to damage DNA than a beta decay. Another factor is that exploding carbon and potassium atoms are spread throughout the body, whereas an ingested radioactive alpha emitting material is going to be somewhat concentrated, for example, the lining of the gut is going to be strongly affected.
Dating
igneous rocks with radioactive potassium
Potassium
40 decay, with its long half life 1.26 billion years, can be used as the
basis to date old and very old rocks. This method, known as potassium-argon
dating, works with volcanic rocks ages 100k years up to nearly the age
of the earth or several billion years. Radioactive decay is an exponential
process. An exponential decay is approximately linear with time for times
less than the half life (or lifetime) (see below). This means a rock that
was last molten 0.001 tau = 0.001 x 1.44 x 1.26 billion years ago = 1.8
million years ago has converted 0.001 or 1 part in a thousand, of its potassium
40 to argon 40.
When rocks are molten, it's thought that any argon gas they contain will escape, so all the argon found in a rock is assumed to have come from the decay of potassium 40. The ratio of potassium 40 to argon 40 in a rock therefore provides a means to date when the rock was last molten. The procedure melts the rock sample and measures the freed argon with a mass spectrometer. The potassium concentration is measured differently in a second step.
Curious facts
about argon
Almost 1%
of the earth's atmosphere is argon. What? Where did all this argon come
from? It's nearly all argon 40 (99.6%), and according to Wikipedia nearly
all of comes from down conversion (positron emission) of radioactive potassium
40. Potassium 40 has a 1.2 billion half live and mostly it up converts
(beta decay) to calcium 40, but 11% of the time it down converts to argon
40, which being a noble gas just accumulates in the atmosphere.
What is curious is that most (85%) of the argon in the sun is a different isotope (argon 36), so presumably on the sun it arises from a nuclear process.
Argon-argon dating method
Recently the
dating process with potassium has been improved. The new method is called
the argon-argon dating and is usually more accurate than potassium-argon
dating and it works with a smaller sample. First the sample is irradiated
in a nuclear reactor. This converts (by irradiating with a flux of beta
rays?) a known fraction of common isotope potassium 39 in the sample to
argon 39. Then one instrument (mass spectrometer) can determine the age
by measuring the ratio of argon 40 (from decay of radioactive potassium
40) to argon 39 (created by the reactor flux from potassium 39).
Dating early hominid fossils
The potassium-40
based dating methods are the preferred means to date early hominid fossil
bones (from Africa), which are in the range of 1 to 6 million years old.
The dating is not done on the bones themselves, but on the rock and dirt
in layers above and below where the fossils are found. For these methods
to work the rock and dirt samples must contain some fallout from volcanos.
Fossils are only preserved in sedimentary rock (rock built up by the gradual
accumulation of small particles), so the quantity of volcanic material
is generally small. Paleontologists sometimes choose fossil beds near volcanos
to improve the dating. If the rock and dirt does not contain (enough) volcanic
fallout, then hominid fossil dating must be done by comparison with associated
ancient animal fossils which may have radioactive dates from other sites.
The comparison method is not as accurate as the potassium dating methods.
Exponential decay (tau vs half life)
Many decay processes in nature follow an exponential curve (e^-t/tau),
for example, radioactive decay and the decay of the voltage on a capacitor
bleed by a resistor. This formula pops up whenever decay rate depends (linearly)
on the quantity that is decaying. For example, take the case of a charged
capacitor with a resistor across the capacitor (in parallel). The current
in the resistor, by ohm's law, depends linearly on the voltage (i=V/R).
This means the current 'bleeding' down the charge in the capacitor falls
as the voltage on the capacitor falls. The result is that the voltage falls
exponentially with time, initially quickly but then tapering off to a slow
tail. The capacitor discharge voltage is v = (initial voltage) x e^-t/tau,
where tau = RC.
For unknown reasons (probably historical) engineers and physicists characterize the same exponential curve differently. Engineers use time tau, known as the lifetime. This is the point on the curve when the decaying parameter has decayed to about 37% (or e^-1) of its initial value. Physicists use half life, which is the point on the curve when the decaying parameter has decayed to 50% of its initial value. The physicist's value may seem simpler, but the engineer's value makes calculation and estimation easier.
engineers e^ -t/tau
= e^-1 = 0.3679 (t = tau)
physicts 0.5 = e^-t/tau (where t=half life)
ln (0.5) = ln (e^-t/tau)
ln (0.5) = -t/tau x ln (e)
-0.6931 = -t/tau x 1
half life = 0.6931 tau
relationship tau = 1.4427 half life
One of the reasons engineer like and use tau is that it
provides a simple approximation to the exponential without scaling constants.
For example
slope of e^ -t/tau (@ t=0) = -1/tau
This means the initial decay is just a simple fraction of the lifetime (tau), for example, for time of 1% of tau decay is (about)1%, and for time of 10% of tau decay is (about)10%, etc.
Integral of e^ -t/tau (0 to infinity) = tau
Calculating
Alpha Particle Parameters
Alpha particles
are quantum mechanical, but surprisingly (to me) simple classical physics
equations applied to alpha particles seems to give reasonable answers.
We can figure the number of atom in 1 gram of radium-226 from the reference disintegration rate of 1 curie (37 billion disintegrations). The decay rate of any isotope when plotted vs time follows an exponential decay. Since the slope of e^-t/tau = -1/tau @ t=0 that means that if the disintegration rate remained constant at the initial rate all the atoms of a sample will have decayed at t=tau. So to figure the number of atoms in a sample we only need multiply the ininitial disintegration rate by the tau. For radium-226
tau = 1.4427 x half life
= 1.4227 x 1,620 yr
= 1.4227 x 1,627 yr x 3.156 x 10^7 sec/yr
= 7.31 x 10^10 sec
# of atom in gram of radium-226
= 37 billion x tau
= 3.7 x 10^10 disintegrations/sec x 7.31 x 10^10 sec
= 2.70 x 10^21
Avogadro's number is the number of atoms in a 'mole', this is the weight in grams equal to the atomic weight. For example, a mole of carbon-12 atoms is 12 grams, a mole of hydrogen atoms is 1 gram. So we need to multiply the atoms/gram x 226.
# of atom in mole of radium-226
= 2.70 x 10^21 x 226
= 6.10 x 10^23
How did we do? The official value for Avogadro's Number
is 6.022 x 10^23, so we came within 1%!
-------------------------
Rather than look up the joule equivalent of Mev used by physicists I will figure it from energy and power equations used by electrical engineers. Power is flow of energy per second. (P = dE/dt) In electrical systems power is current times voltage (P = I x V). Current is flow of charge per second (I = dQ/dt). Units are energy in joules, power in watts, current in amps, voltage in volts, charge in coulombs. Putting it all together we can write
dE = P x dt
= I x V x dt
= dQ/dt x V x dt
dE (in joules) = dQ (in coulombs) x V (in volts)
The charge of an electron is 1.6 x 10 to -19th coulomb. An alpha particle has two protons so it has the same charge as two electons (with opposite sign) or 3.2 x 10 to -19th coulomb. We'll take the 5 MeV as the energy. The electric field radiating from protons (and electrons) has units of volts per meter. Physicists use electron volts as a measure of energy. It has a well defined physical meaning: 'an electron volt (ev) is one electron accelerated through a potential difference of one volt'
From the equation the energy in joules of 1 ev is therefore the charge of the electron in coulombs times 1 volt.
energy in joules = coulomb x volt
= 1.6 x 10^-19 coulomb x 1 volt
Check (from online references)
1ev
= 1.6 x 10^-19 joule
so for a 4.8 Mev alpha particle the energy is
energy in joules = 3.2 x 10^-19 coulomb x 4.8 x 10^ 6 volt
= 15 x 10^-13 joule
= 1.5 x 10^-12 joule
E field has units of volts/meter. I will assume the E
(av) field decreases linearly with radius.
E = 1/2 x 4.8 Mev/ radius of radium (m)
= 1/2 x 4.8 x 10^6 volt/0.215 x 10^-9 meter
= 11.1 x 10^15 v/m
= 1.11 x 10^16 v/m
Force on particle in newtons is
F = q x E
= 3.2 x 10 ^-19th coulomb x 1.2 x 10^16 volt/meter
= 3.8 x 10^ -3 newton
Force = mass x accel = mass x dv/dt. Hence
dv = force x dt/mass
= 3.8 x 10^-3 newton x 2 x 10 ^-18th sec/6.7 x 10^(-27) kg
= 1.1 x 10^6 meter/sec
Is this 20% of the speed of light?
alpha
speed = 0.2 x 3 10^8 meter/sec
= 6 x 10^7 or 60 x 10^6
Not too good, our calculated velocity is too low by a factor of about 50.
Using the 37 billion decays per sec for one gram of radium we can now find out how many watts the radium (only) self-heats (assuming that almost all the 5 Mev alpha particles are absorbed by the sample)
power in watts = energy in joules per second
= 37 x 10^ 9 decays/sec x 1.6 x 10^-12 joules/decay
= 59 x 10 to -3rd
= 59 mw (radium decay only)
The above is the energy from the radium decay only. It ignores the energy from the decay of daughter products. The next five decays occur fast. The first and slowest is the decay of radon in 3.8 days. The next four are all minutes or less. Even though radon is a gas if the sample is solid these distributed atoms are probably trapped in the sample. So unless the radium sample has just been freshly prepared, for each radium decay there is about five more decays further down the chain to the interim isotope lead 210, which has a 22 year half life. The five decays from radon down to lead 210 emit five times the energy of the radium decay itself, raising the total energy output of the sample to 6 times the value calculated above
power in watts = 6 x 59 mw
= 354 mw (radium + five daughter decays)
A calorie is defined as the amount of energy required to raise the temperature of 1 gram of water 1 ?C. The conversion between calories and joules is 1 calorie = 4.19 joules. Let's find out how long it will take for 1 gm sample of radium to output 1 calorie of heat. Power = dE /dt, so time is energy divided by power
time = 1 calorie/354 mw
= 4.19 joule/0.354 watt
= 11.8 seconds
This is a heat output rate of (3,600 sec per hr/11.8 sec) = 305 cal/hr
How does this agree with the measured value? Not too bad. In the early 1900's the energy output of 1 gram radium samples were measured to be in the range of 134 to 140 cal/hr. So starting with the 37 billion radium decays/sec reference and including all the five fast daughter's energy we calculate sample energy about 2.2 higher than the measured value.
Radium daughter's energy
Radium atoms
are created by the decay of uranium 238 (U 238), the most common isotope
of uranium, at essentially a constant rate, since the lifetime of U 238
is about five billion years. It takes five decays from U 238 to create
radium 222 (Ra 222), the most common isotope of radium with a half life
about 1,600 years. It takes nine more decays from Ra 222 to reach the stable
isotope of lead (Pb 206). Here is a list of the elements from uranium to
lead in order by atomic number.
| U | uranium | 92 |
| Pa | protactinium | 91 |
| Th | thorium | 90 |
| Ac | actinium | 89 |
| Ra | radium | 88 |
| Fr | francium | 87 |
| Rn | radon | 86 |
| At | astatine | 85 |
| Po | polonium | 84 |
| Bi | bismouth | 83 |
| Pb | lead | 82 |
An alpha decay thows off two protons lowering the atomic number by two and the atomic weight by four since two neutrons are also thown off. A beta decay thows off a negatively charged electron, which increases the atomic number by one and leaves the atomic weight (pretty much) unchanged..
The dominant decay chain from radium to stable lead 206 is below. Notice the pattern. It's like three big jumps with two little bounces. Radium (atomic number 88) drops to lead (atomic number 82) in three jumps via three alpha decays, but this is lead 214, which not stable. Lead then converts up two to polonium via two beta emissions. Polonim 214 drops down to lead 210 with an alpha emission. Lead (210) again converts up two to polonium (210) with two beta emissions. Polonium 210 via an alpha emission drops down to lead 206, which is stable. Here is the pattern with the half lives and energy.
Nuclide Decay Mode Half life MeV Product of decay
Ra 226 alpha
1,602 yr 4.871
Rn 222
Rn 222 alpha
3.8235 day 5.590
Po 218
Po 218 alpha
3.10 min 6.615
Pb 214
Pb 214 beta
26.8 min 1.024
Bi 214
Bi 214 beta
19.9 min 3.272
Po 214
Po 214 alpha
0.1643 ms 7.883
Pb 210
-------------
29.255 Mev
Pb 210 beta
22.3 yr 0.064
Bi 210
Bi 210 beta
5.013 day 1.426
Po 210
Po 210 alpha
138.4 day 5.407
Pb 206
Pb 206 -----
stable
Notice that the first five decays after radium are fast, one 3.8 days and the others minutes or less. This means that in a few weeks after a radium atom has decayed it will likely see five more decays talking it down to lead 210 where things will slow way down as lead 210 has a 22 year lifetime. These daughter decays put out about five times more energy than the original radium decay, so if the decayed atoms remain in the sample, which is likely if the sample is a solid, then the energy outupt of the sample is really about six times higher than the energy output from the radium decay (29.255 Mev vs 4.871 Mev).
The Wikipidea link to the 'radium series' decay chain, which includes the decay sequence above, is here
http://en.wikipedia.org/wiki/Decay_chain#Radium_series
We can calculate the speed of the alpha particle from
it kinetic energy and its mass.
mass of proton
: 1.67 x 10^-27 kg
mass of alpha
particle = 4 x 1.67 x 10^-27 kg
= 6.7 x 10^-27 kg
kinetic energy
of alpha (4.8 Mev) = 1.5 x 10^-12 joule
kinetic energy
(in joules) = 1/2 x mass (in kg) x (speed in m/sec) squared
speed (in
m/sec) = rt{2 x kinetic energy (in joules)/mass (in kg)}
= rt{2 x 1.5 x 10^-12 joule/6.7 x 10^-27 kg}
= rt{0.48 x 10^15}
= rt{4.8 x 10^14}
= 2.19 x 10^7 m/sec
alpha speed/light speed = 2.19 x 10^7 m/sec/3 x 10^8 m/sec
= 7.3% of speed of light
The references usually say the speed of an alpha particle is approximately 5% (1/20th) of the speed of light, which is 1.5 x 10^7 m/sec. A reference on Rutherfords' scattering experiment gives alpha particle speed at 1.9 x 10^7 m/sec. Another reference on alpha particles gives 2.06 x 10^7 m/sec. Our calculation from 4.7 Mev yields 7.3% speed of light. Don't know why we don't get better agreement.
We can crosscheck the energy value with the speed since all the energy we are concerned with is carried by the kinetic energy of the particle. The formula for kinetic energy of a mass is 1/2 x mass x speed squared. It's easy to find the mass of a proton in a web search. An alpha particle with two protons and two neutrons has about (within 1%) the mass of four protons. The speed of an alpha particle is quoted as (about) 1/20 speed of light.
mass of proton
: 1.67 x 10^(-27) kg
mass of alpha
particle = 4 x 1.67 x 10^(-27) kg
= 6.7 x 10^(-27) kg
kinetic energy
= 1/2 x mass in kg x (speed in m/sec) squared
= 0.5 x 6.7 x 10^(-27) kg x (0.05 x 3 x 10^(8)m/sec)^2
= 0.5 x 6.7 x 10^(-27) kg x (1.5 x 10^(7)m/sec)^2
= 7.5 x 10^(-13) joules
This agrees pretty well (factor of 2) with the 5 Mev energy
value of 16 x 10^(-13) joules
volt = energy/coulomb
= 7 x 10 to 6th/(2 x 1.6 x 10 to -19th)
= 2 x 10 to 25th volt
Tunning refers to the fact that a particle, which in classical terms does not have enough energy to cross a barrier or in the case of an alpha particle does not have enough energy to escape the strong nuclear force holding it in the nucleus, can be calculated using quantum mechanics to a non-zero and usually tiny probability of crossing the barrier.
A speculative, but I think reasonable assumption, is that when the alpha particle first exits (by tunneling) the nucleus is has almost no speed or kinetic energy. Once the alpha paricle is just outside the grip of the short range strong force it will be accelerated away as both it and the nucleus have positive charge and like charges repel, and since the nucleus is large with 86 (remaining) protons the accelerating E field is high. of As the alpha particle accelerates across the atom radii the force on it will go down as it will 'see' more and more of the negative charge of the atom. We can further assume that when it reaches the edge of the atom, it stops accelerating, because the atom negative charge in the electron cloud now balances (or almost balances) the positive charge in the nucleus. Because this is just an order of magnitude calculation we'll make a simplifying assumption that the force on the alpha particle within the atom is constant at the average value. With our assued constant force and zero intial speed the velocity profile acorss the atom radius is a linear with the final value 1/20 speed of light. The average speed is half the final speed. We have the radius of a large atom in the graph above.
time (to transit atom radius) = radius/{0.5 x 1/20 (3 x 10 to 10th cm/sec}
= 2 x 20 x 0.15 x 10 to -8th cm/3 x 10 to 10th cm/sec
= 2 x 10 to -18th sec
10 to -18 sec os pretty dam faast. We can now the calculate
our one particle current.
(????)
amps = alpha coulomb/ time to transient radius in sec
= 3.2 x 10 to -19th/2 x 10 to -18th
= 0.32/2 x 10 to -1
= 0.016 amp (16 ma)
Lets find the energy in the alpha particle in joules which is watt x sec
Joules (alpha particle) = watt x time = amp x volt x time
= (16 x 10 to -3rd) x (2 x 10 to 25th) x (2 x 10 to -18th)
= 64 x 10 to 4th
Wikipedia on alpha particle
http://en.wikipedia.org/wiki/Alpha_particle
---------------------------------------
Wikipedia in detailed radium specs list radii of radium
as 215pm which is .215 nm
2nd experiment is Bohr's orbit jump equation and the spectrical emission frequencies of hydrogren
My outline for atomic development was culled from the excellent book Great Physicists: The Life and Times of Leading Physicists from Galileo to Hawking by William H. Cropper.
Nuclear ? Particle Physics Timeline
http://www.physics.northwestern.edu/Phyx103/web/nuc-timeline.html
Introductions to atoms with history
http://www.scienceclarified.com/everyday/Real-Life-Chemistry-Vol-1/Periodic-Table-of-Elements.html
Radium heat output
www.spacecatalog.biz/about3112-675.html
Reference
mass
atomic weight
rest mass energy
Proton
1.6726 x 10^-27 kg
1.0073
938 Mev
Neutron
1.6749 x 10^-27 kg
1.0087
939 Mev
Electron
0.0009 x 10^-27 kg
0.0005
0.51 Mev
q (charge of electron ? proton) 1.60 x 10-19 coulomb
1 Mev 10^6 x 1.6 x 10-19 joule = 1.60 x 10-13 joule
Rest mass energy
of a proton (E=m x c^2)
E = 1.67 x 10^-27 kg x (3 x 10^8 m/sec)^2
= 1.50 x 10^-10 joule
= 1.50 x 10^-10 joule x 1 Mev/1.60 x 10-13 joule
=938 Mev (approx 1,000 Mev)
Coulomb's law
--- electrostatic repulsion between like charges
F = k x q1 x q2 /r^2
where
k = 1/(4 x pi x e0) = 9 x 10^9 N m^2 c^-2 (also F m^-1)
(e0 = 8.8 x 10^-12 )
f
is newtons, q is coulombs, r is meters
Lorentz law
--- force on a charge (q) due to electric (E) and magnetic (B) fields
F = q (E + vel cross B)
where
f
is newtons, q is coulombs, E is volts/meter, B is tesla
or webers/m^2
Dimensionless
constants
ratio of proton mass/electron mass = 1836 (1,836.152701)
fine structure constant (xxxx) = 137 (137.0359895)
atomic weight of oxygen-16
Protons
8 x 1.0073 = 8.0584 +
Neutrons
8 x 1.0087 = 8.0696 +
Electrons 8
x 0.0005 = 0.0040
------------------
Oxygen atom atomic weight 16.132
----------------------------------------------------------------------------
Mass puzzle of protons and neutrons
Neutrons and
protons are both are made up of up and down quarks, which means up and
down quarks (with leptons like electrons) make up virtually the entire
universe.
neutron
udd (one up, two down)
proton
duu (one down, two up)
The neutron is 0.1% heavier than the proton, but I read in Scientific American that 'd' (down quarks) are twice as heavy as 'u' (up quarks). Is that right? (Yes, Wikipedia agrees) Then how (the hell) can the neutron only be 0.1% heavier than the proton? If we simplistically say u =m and d = 2m, then we find the neutron = m + 4m = 5m and the proton = 2m + 2m = 4m. This would mean the neutron 'should be' 25% heavier than the proton, but it's not. Something is weird.
The mystery deepens (in two ways) when we look at the quark masses in Wikipedia: 'd' = 3.5–6.0 MeV, 'u' = 1.5–3.3 MeV. One, they both have almost a factor of two uncertainty, and two, the quark masses (total for the three) are only 1 to 2% of the proton and neutron's mass! So where's the missing mass/energy, in the kinetic energy of the quarks? No apparently (see below) it is in the 'strong' field between them! Wikipedia (Down Quark) says this about the mass 'mystery':
"When found in mesons (particles made of one quark and one antiquark) or baryons (particles made of three quarks), the effective mass (or 'dressed' mass) of quarks becomes greater because of the binding energy caused by the gluon field between each quarks. For example, the effective mass of down quarks (up quark too) in a proton is around 330 MeV. Because the bare mass of down quarks is so light, it cannot be straightforwardly calculated because relativistic effects have to be taken into account" (The physicist authors of the Scientific American article made an off hand comment that calculating the mass of the proton and neutron quantum mechanically is very difficult.)330 Mev 'effective' mass looks strange too. Now the masses are too high by 5.5%! (No clue why)
proton
duu
938 Mev ?=?=> 990 Mev = [330 + 330
+ 330]
-----------------------------------------------------------------------------
Periodic table with a twist --- light spectrum of every
element (Neat applet)
http://jersey.uoregon.edu/vlab/elements/Elements.html
=========================================================
Outline for a HS talk
Brief history of atom and intro to quantum mechanics
Thumbnail atomic history 1897 to 1932
Thumbnail sketch tracing how the the inside of the atom was figured out
Thomson (negative particles in cathode ray tubes), Rutherford (small positive center), Bohr (quantized electron orbits) deBroglie (electrons have wavelength which fit in Bohr's orbits) Schrodinger (develops an equation for deBroglie's wave, but doesn't know what it means), Born (suggests Schrodinger's wave equation gives probability), Heisenberg (ties it all together with his 'uncertainty' principle), Chadwick (unusually penetrating radiation from atoms). For a classroom talk a neat wrap up is would be show the class how the Heisenberg Uncertainty Principle allows the velocity of electrons in atoms to be almost trivially calculated.1756 Franklin -- experiment with oil
1900 Plank -- explains 'hot poker' or black-body radiation
assumes light energy reflection and absorpton (by electrons) is quantized
(whole cycles)
E = h x freq
h = 6.6 x 10^-34 joule-sec (Planck's constant)
delta E = h x 1 cycle/sec = 6.6 x 10^-34 joule
1905 Einstein -- explains photoelectric effect
light is physically quantized (into photons) according to Plank's formula
1911 Rutherford -- experiments with alpha particle deflection
positive charge concentrated in a tiny center ('fly in a cathederal')
1913 Bohr -- explains frequency of hydrogen light emissions
(Balmer series)
assumes angular momentum of electrons can only be multiples of plank's
constant
[m v r = n h] where n = 1,2,3...
implies
a) (circular) orbits of hydrogen electrons are quantized
b) hydrogen light emissions are 'explained' as photons emitted by electrons
'jumping' to lower orbits
c) hydrogen 'expands' with radius increasing as n^2
velocity goes as 1/n, (KE = 1/2 m v^2) goes as 1/n^2
electron velocity in lowest (n=1) orbit = 0.7% c
kinetic energy (KE) in n=1 orbit = 13.6 eV
potential energy (PE) = - 2 KE
(PE =0 is at infinity)
total energy = (KE + PE) = KE - 2 KE = - KE
jump from n=2 to n=1 orbit emit a photon with energy
E (n=2) - E (n=1) = photon energy
-(1/4) 13.6 eV - (-13.6 eV) = (3/4) 13.6 eV = 10.2 eV
1924 de Broglie-- guesses electrons (all matter) have
an associated 'wave'
wavelength depends on the speed of the particle [wavelength = h/mv]
1925 Heisenberg -- 1st version of quantum mechanics (theory
of how light and electrons interact?)
very abstract (based on matrix mathematics)
1926 Schrödinger -- 2nd version of quantum mechanics
(based on waves)
invents a formula that when solved for de Broglie waves in hydrogen
shows the shapes of all the hydrogen orbits (s, p, d, f orbitals)
1926 Born -- suggests that Schrödinger wave is best
understood as a probability
it gives the statistics that will result when an quantum (or atomic) experiment
is repeated many times
1927 Heisenberg -- Heisenberg 'uncertainty' principle'
principle
-----------------------------------------------------------------------------
---------------------------------------------------------------------------------------------
* Quantum mechanics is developed to solve two problems:
a) Theory of electrons in atoms
b) Theory of how light interact with electrons
* Planck -- Quantizes the exchange of energy between light
and matter
To model light being
absorbed and emitted inside a hot furnace (black body radiation) he assumes
the walls contain oscillators (now known to be electrons) that exchange
energy with the light in little energy packets (quanta) and that:
a)
Each cycle exchanges a fixed amount of energy (6.6 x 10^-34 joule)
b) Partial cycles don't count (no energy is exchanged)
Equations
a) Energy quanta/cycle = h x 1 cycl/sec = 6.6 x 10^-34 joule
where
'h' is now known as Plank's constant
b) Energy quanta (in an exchanged with light) = h x frequency (of light)
* Einstein -- explains photoelectric effect assuming light
is quantized using Plank's formula
Explains the
photoelectric experiment by extending Plank's idea to light photons [E
(photon) = h x frequency]. The (instantaneous) transfer of light photon
energy to electrons (in metal in this experiment) causes light to act like
a stream of particles.
* Einstein -- special relativity
Shows that
since nothing can go faster than speed of light [3 x 10^8 m/sec] it implies
that time mass gets heavier, dimensions contract and time dilates.
* de Broglie -- electron (matter) waves
de Broglie
playing around with the equations of special relativity (and mixing in
plank's equation) finds that if there was a was wave associated with electrons
(or any matter) that it would be consistent with special relativity, so
it suggests in his Phd these maybe such matter waves might exist. And he
pulls out a formula for the wave frequency. His advisors are baffled and
ask Einstein for his opinion. Einstein replies with a famous quote, de
Broglie has "lifted the corner of a great veil". Not long after electrons
are found to exhibit wave like interferance when refracted off cyrstals
with the wave frequency that de Broglie equation predicts.
Equation
wavelength = h/p
where
h = plank's constant
p = momentum (m x v)
de Broglie's waves fit beautifully into Bohr's hydrogen orbits, and (to a large extent) explain why the orbits are quantized in just the manner that Bohr had assumed.
* Heisenberg -- 1st quantum mechanics theory
Heisenberg
comes up with the 1st formulation of quantum mechanics (electrons and light
interaction). It's a pure math theory (uses matrixes) with no underlying
physical model or picture. It gives the right answeres but pretty much
everyone hates it because it give no insight as to how electrons and light
interact.
* Heisenberg -- Uncertainty Theory
A couple of
years later Heisenberg finds hiding in his equations a very simple formula
that greatly simplifies many calculations and has huge philosophical implications
for what can be known in the quantum world.
Equation
(delta p) x (delta x) > hbar
where: p = mass x velocity, hbar = h/(2 pi)
Heisenberg uncertainty applied to electron in hydrogen
v = hbar/m r
= (1.05 x 10^-34/9.1 x 10^-31)/radius
m = 9.1 x 10^-31 kg (electron mass)
= 1.15 x 10^-4/radius
= 1.15 x 10^-4/53 x 10^-12
set radius = 53 pm (Bohr radius)
= 0.0217 x 10^8 m/sec
c = 3 x 10^8 m/sec (speed of light)
= 0.7% c (speed of light)
-----------------------------------------
Playing with the three key equations (factor of 2 mising)
delta p delta (2 pi r) = h
L = m r v = hbar
wavelength = h/mv
E = h freq = h v/wavelength = h v /(h/mv) = m v^2 = 2E ?
These equations imply that momentum and energy are quantized
(for a confined particle with standing waves and light too) .
Looks like de Broglie wavelength is equivalent to quantify
kinetic energy
wavelength = h/mv
v/freq = h/mv
mv^2 = h freq
E = p^2/2m
p = sqrt{2mE}
wavelength = h/sqrt{2mE}
wavelength^2 = h^2/2mE
2mE = h^2/wavelength^2
2mE = (h/wavelength)^2
wavelength = 2 pi r
-- Erwin Schrodinger discovered that when frequency f and de Broglie wavelength y were substituted into general wave equations it becomes possible to express energy E and momentum mv as wave functions - thus a confined particle (e.g. an electron in an atom/molecule) with known energy and momentum functions could be described with a certain wave function.=============================================================-- From this it was further found that only certain frequency wave functions, like frequencies on musical strings, were allowed to exist. These allowed functions and their frequencies depended on the confining structure (atom or molecule) that the electron was bound to (analogous to how strings are bound to a violin, and only then can they resonate at certain frequencies).
-- Significantly, these allowed frequencies corresponded to the observed discrete frequencies of light emitted and absorbed by electrons bound in atoms/molecules. This further confirmed the standing wave properties of matter, and that only certain standing wave frequencies could exist which corresponded to certain energy states.
Intro
Ben Franklin experiment in 1700's provides an estimate
of size of atoms
Hard to tell
from the history books, but Ben Franklin was one of the world's great scientist
of the 1700's, totally self taught. When he goes to Paris around the time
of the revolutionary war, he is a celebrity there. Sailing across the Atlantic
to Paris in a convoy of 96 ships, he notices that the ships behind are
sailing smoother than the ships in front. The captain says, oh yes, the
cooks must have thrown out the greasy cook water. What, you mean a few
tubs of greasy water are able to calm the waves of the North Atlantic?
Yup.
Well this gets Ben's attention, and he begins experimenting with oil and water in his rocking cabin, and when he gets to Paris he has the top of his cane hollowed out to hold a teaspoon of oil. And everywhere he goes in Paris he dumps the oil from his cane on ponds and always the calming effect is remarkable. Where the oil covers the water, the water becomes as flat as a sheet of glass.
While Ben was interested in the calming effect a thin coating of oil had on waves in water, his experiment provides an early estimate of the size of atoms. We can calculate the thickness of the oil layer using Ben's own numbers (see notes). The oil thickness comes out to be 2.5 nm, which gives us an upper limit for the size of atoms. It is in fact about x10 dia of a typical atom. We now know the oil spreads out to a thickness of one molecule, and oil is a mixture of short hydrocarbon chains with a typical oil molecule having something like ten atoms.

scan of handwritten page 1 of handout
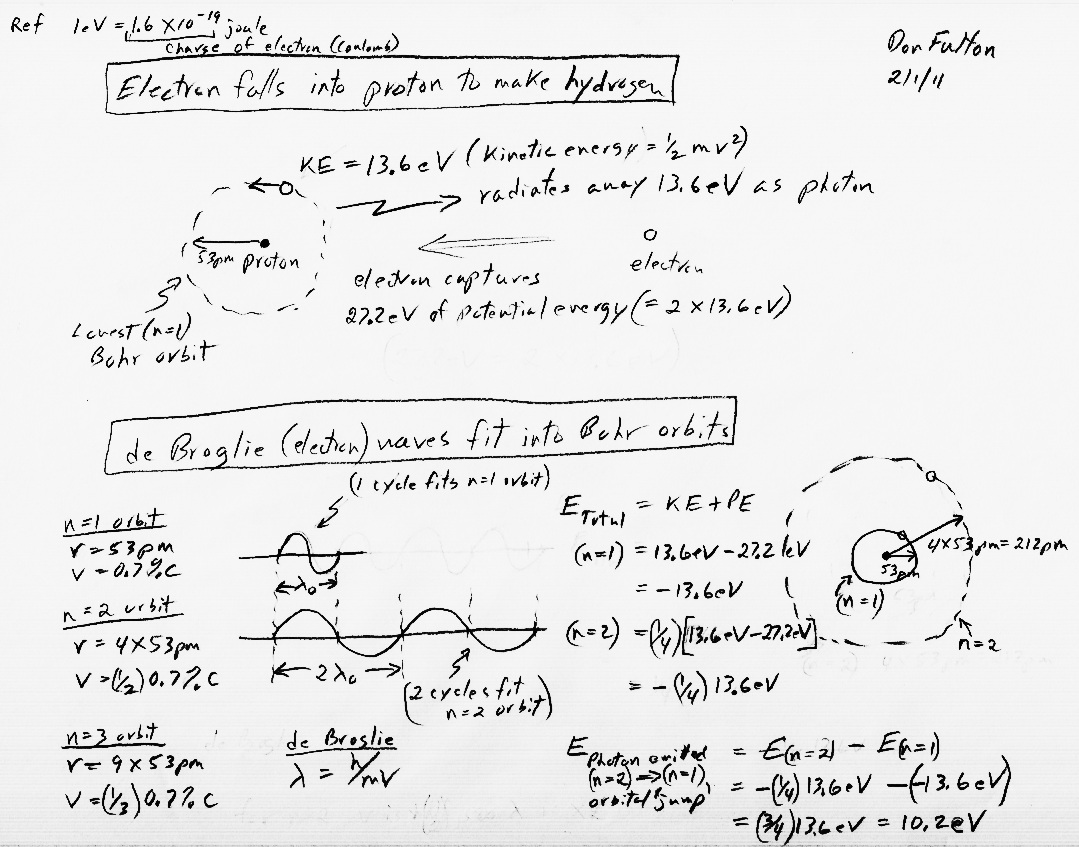
scan of handwritten page 2 of handout
1756 Franklin -- atom size estimate
Ben Franklin
shows atoms can be no bigger than about 2.5 nm by pouring a teaspoon
(5 ml) of oil on a pond and estimates it spreads to cover 1/2 acre (acre
= 4,000 m^2).
teaspoon oil vol
cylinder (1 cm^2 area x 5 cm deep) = 5 x 10^-6 m^3
1/2 acre (area)
2,023 m^2
oil thickness
vol/area = 5 x 10^-6 m^3/2,023 m^2 = 2.5 x 10^-9 m = 2.5 nm
1897 Thomson -- cathode rays are electrons
JJ Thomson
tests cathode rays and finds they are negatively charged particles (indicated
by direction in which they are bent by a voltage) and it doesn't matter
what trace gas he starts with. From degree of bending he can estimate (e/m)
and by measuring the heat carried by the electrons he can estimate 'm'
(since KE = (1/2) m v^2). He estimates electrons are roughly 1,000 times
less massive than hydrogen atoms. (1906 Nobel prize for physics)
1900 Plank -- light emitted in quanta (by unknown 'oscillators',
one quanta per cycle)
Max Plank
in deriving an equation for black body radiation (spectrum of radiation
vs temperature)finds he can only fit the data if he puts two restrictions
on the how light is emitted from 'oscillators' (later understood to be
electrons). (1918 Nobel Prize in Physics)
a) Light energy is linear with frequency (slope is 'h' Plank's constant)
b) No fractional cycles (frequency is quantized in cycles/sec or hertz)
Key equation
E = h x freq
where 'h' is planks constant (6.6 x 10^-34 joule-sec)
(freq in integer cycles)
E quanta =
h x 1 hz (or cyle/sec) = 6.6 x 10^-34 joule
1906 Einstein -- light absorbed by electrons as quanta
(with energy proportional to frequency)
Albert Einstein
uses Plank's equation to explain photoelectric effect (electrons knocked
off metal by light). Light appears to be absorbed by electrons only as
energy quanta with the energy of the quanta proportional to the frequency
(color) of the light. In this sense light looks like a lot of little particles.
(1921 Nobel Prize in Physics)
1911 Rutherford -- positive charge concentrated in tiny
nucleus
Ernest Rutherford
in a famous alpha recoil experiment fires alpha particles (helium nuclei)
at atoms (in gold foil) and measures how they are deflected. Finding that
most just pass through, but a tiny fraction are deflected, and a few of
these actually bounce back, he concludes that most of the mass of the atom
(and all the positive charge) must be concentrated in a tiny region in
the center (dia less than 1/10,000 dia of the atom). Thus most of the volume
of the atom is the negative electrons which must be moving around, in some
sense orbiting the nucleus, so they don't fall into the postive center
(to which they are attracted). (1908 Nobel Prize in Chemistry)
1913 Bohr -- electron 'orbits' quantized
Neils Bohr
comes up with a model where electrons are moving in circular orbits, but
he adds an (ad hoc) restriction using the constant ('h') from Plank's light
equation that only certain orbital radii are allowed. (Technically he quantizes
angular momentum [m v r = n h, where n = 1.2.3...], but v can be calculated
from r,so he can calculate the allowed orbital radii and electron energies.
He finds this model of the atom is able to explain all the known line emissions
of hydrogen (Balmer series of lines) as being due to energy lost or gained
as electrons 'jump' between orbits. The model also predicts new hyrogen
lines and they are found. (1922 Nobel prize for physics)
1924 de Broglie-- matter waves
Louis de Broglie
in his Phd thesis suggests that electrons may have an associated 'wave'.
He has a formula for its wavelength [wavelength = h/mv]. It is found that
de Broglie's electron wavelengths fit perfectly into the Bohr's hydrogen
atom orbits forming standing waves: one wavelength in the first orbit,
two in the next higher energy orbit, etc. (1929 Nobel Prize in Physics)
1925 Heisenberg -- 1st version of quantum mechanics
Werner Heisenberg
comes up with an abstract mathematical fomulation of quamtum mechanics
called matrix mechanics. It does provide numbers that match experiments,
but most people hate it provides no 'picture' or model to explain how electrons
and light interact. (1932 Nobel prize for physics)
1926 Schrödinger -- Schrödinger wave equation
& 2nd version of quantum mechanics
Erwin Schrödinger
mathematically comes up with a wave equation for electrons in the atom.
When solved for hydrogen, it gives all the orbital shapes ('s', 'p', 'd'
and 'f' orbitals) you find in textbooks. People like this 2nd versioin
of quantum mechanics, because physicists understand waves. Problem is:
It is not clear what is 'waving' (1933 Nobel Prize in Physics)
1926 Born -- Schrodinger/de Broglie wave indicates probability
Max Born suggests
that Schrodinger's and de Broglie's wave (when squared) just gives the
probability of finding an electron in a specific region of space. It is
not really a 'physical' wave. Schrodinger disagrees, he thinks his equation
shows shows how an electron is spread out. (1954 Nobel prize for physics)
1927 Heisenberg -- Heisenberg 'uncertainty' principle'
-- Werner
Heisenberg comes up with a simple formula that becomes a cornerstone of
quantum physics. It tells what we can know, and not know, about a particle
in the quantum world. Besides providing physical insight, it allows some
problems, like how fast an electron moving in a specific orbit, to be simply
solved. Uncertainty principle says flat out that it is impossible
to know (to measure) at any one time accurately both the location and motion
(velocity) of an electron. [One form is (delta x) (delta mv) > h/2 pi,
but there are other forms (delta E) (delta time) > h]
For example, the smaller we make an orbital radius (delta x getting smaller), then the faster the electron in that orbital must move (delta v getting larger) to keep the product larger than the Plank's constant. The inner electron orbital in uranium (element #92) is almost 100 times smaller (in radius) than the electron orbital in hydrogen, so according to the Uncertainty principal the inner electrons in uranium must be moving almost 100 times faster than in hydrogen, and they are. (Hydrogen (#1) electron moves at 0.7% speed of light and inner electron speed in uranium (#92) is 70% of the speed of light).
1927 -- Uncertainty principal shows electron orbits are
'fuzzy' (orbitals)
The Heisenberg
uncertainty principal applied to the electron 'orbits' shows we need to
consider the orbits as spread out ('fuzzed out'). The Bohr electron orbits
are in some sense the center of the orbits, just the most likely
regions to find the electron, basically the center of the radial 'fuzz'
zone. First orbit (n=1) center at ao (Bohr radius) extends from 0 (approx)
to 2ao, 2nd orbit (n=2) center at 4ao extends from 2ao to 6ao, 3rd orbit
(n=3) center at 9ao extends from 6a0 to 12ao, etc.
1932 Chadwick discovers neutron in nucleus
James Chadwick
finds a a previously unknown particle coming out of the nucleus of the
atom. Tests show is uncharged and heavy with a mass in the range of the
proton.
Chadwick bombards a thick layer of beryllium (element #4) with high energy, high speed (5% speed of light) alpha particles from a tiny bit of intensely radioactive polonium (138 day half life). He finds the beryllium is emitting a stream of high energy, high speed (some at 10% speed of light) particles that are uncharged. Unlike electrons these particles can travel several inches through air, are not deflected by electric or magnetic fields, and they have high mass because they are able to knock free protons (detected as a pulse of positive current) from the nuclei of many different elements. (1935 Nobel prize for physics)
1948 Feynman --3rd version of quantum mechanics (path
integrals). (1965 Nobel Prize in Physics)
----------------------------------------------------------------------------------------------------------------------
Cool quantum images from PBS Brian Green's Quantum
universe (Nov 2011)
electron double slit interference pattern

waves hitting double slit

waves hitting double slit (slightly later in time)