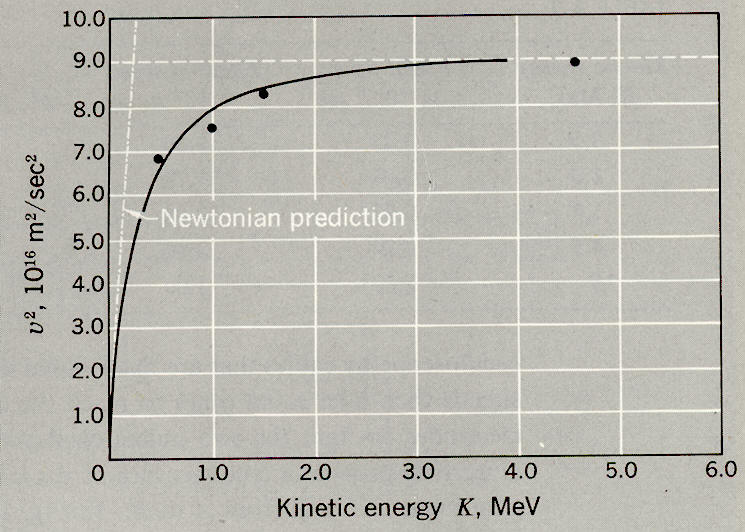
(Speed of electrons)^2 vs energy. Special Relativity
by A.P. French, MIT Introductory Physics Series, 1968
You can't get particles to go faster than 3x10^8 m/sec regardless of how much energy you give them. The speed of light (in a vacuum) is unaffected by the speed of the source of the light. Everybody who measures the speed of light gets the same value, c = 3 x 10^8 m/sec. Special relativity provides a fundamental understanding of these otherwise totally bizarre experimental results.
Nothing can go faster than the speed of light?
(update 11/18/11)
-- see Appendix 'Neutrinos faster than 'c'?)
How to we
know? Well for one thing, it's an experimental fact. Electrons
are very light, charged particles, so are easily accelerated. It
takes less than a million volts and a few feet to accelerate electrons
up to near the speed of light. Acceleration tests on electrons were done
over 50 years ago up to 15 mev with a van de graph generator and room size
linear accelerator at MIT. The speed of the electrons was determined by
measuring how long it took them to move (in a vacuum) between two points
20 feet apart. At the speed of light the distance moved in one nanosecond
(10^-9 sec) is about one foot (0.3 meter), so moving 20 feet would take
20 nsec, and even 50 years ago time could be measured to 1 nsec resolution
using an oscilloscope. The energy carried by the electrons was measured
by having them hit a barrier at the end of the machine and measuring the
temperature rise.
Let's calculate the speed of the 1 mev electrons from classical (Newtonian) mechanics, which has no 'speed of light' limitation. All we need do is set the kinetic energy at 1 mev and solve for velocity, but because we want to use standard MKS units (length in meters, mass in kilograms, and time in seconds), we first we need to convert ev to joules
Charge of an electron = 1.6 x 10^-19 coulomb
Mass of an electron = 9.1 x 10^-31
kg
1 mev = charge of electron (coulomb) x one million volts
= 1.6 x 10^-19 coulomb x 10^6 volt
= 1.6 x 10^-13 (joule)
E (kinetic energy in joules) = 1/2 x mass (kg) x velocity (meter/sec)^2
solving for velocity
velocity = sq root {2 x E (joule)/mass (kg)}
= sq root {2 x 1.6 x 10^-13(joule)/9.1 x 10^-31 kg}
= sq root 0.35 x 10^18}
= 0.59 x 10^9 meter/sec
= 5.9 x 10^8 meter/sec
Our calculated speed of 5.9 x 10^8 meter/sec is about twice the speed of light (3 x 10^8 meter/sec) in a vacuum. Is that what is measured? No! At 1 mev the measured elctron speed is about 2.83 x 10^8 m/sec), which is 94% of the speed of light. In fact the measured speed came out less 3 x 10^8 m/sec at 15 mev and always comes out less than 3 x 10^8 m/sec regardless of how much energy you give the electrons. This is a very remarkable result!
Since kinetic energy in classical mechanics is proportional to velocity squared, if you plot velocity vs sq root {energy} or plot velocity squared vs energy, you get a straight line. Here is the measured electron speed vs energy taken 50 years ago (plotted as speed squared vs energy). The diagonal white line to the left is the classical speed prediction. Our calculated 5.9 x 10^8 m/sec for 1 mev electrons squared is 35 x 10^16 (m/sec)^, so it is above the maximum of this graph.

(Speed of electrons)^2 vs energy. Special Relativity
by A.P. French, MIT Introductory Physics Series, 1968
The plot clearly shows that as energy increases the speed increases get less and less with the speed gradually (asymptotically) approaching a hard speed limit. The plot's asymptote limit is labeled 9 x 10^16, the square of 3 x 10^8 m/sec, usually represented as c, the speed of light in a vacuum.
It turns out the hard speed limit we measure for the electron is found for any particles and any amount of energy! What is going on here? Well, Einstein (with help from Maxwell) figured it out a century ago, and he figured it out before the acceleration experiments were run!
Riff on electrons in a radio tube --- In tubes used in old radios electrons are 'boiled' (thermally excited) off the cathode and accelerated through the vacuum in the tube to the positively charged plate. The plate is typically about 100 V above the cathode, so during the acceleration the electrons pick up about 100 ev of energy. Guess how fast the electrons are going when they hit the plate?Proof that speed of a light source does not change the speed of lightWell, we can figure the answer in our head --- Kinetic energy goes as vel^2, so vel goes as sq rt (energy). 100 ev is 1 Mev divided by 10^4, so scaling from the 1 Mev example above, the vel in the tube must be (200% speed of light)/sq rt (10^4) = 200% c/100 = 2% speed of light. Yup, in the typical radio tube with a measly 100V electrons are accelerated in one inch to 2% of the speed of light, or 6 x 10^6 m/sec (3,700 mile/sec)!
Check
100 ev =?= 1/2 x m x vel^2
10^2 volt x 1.6 x 10^-19 coulomb =?= 0.5 x 9.1 x 10^-31 kg x [6 x 10^ 6(m/sec)]^2
1.6 x 10^-17 =?= 164 x 10^-19
1.6 x 10^-17 = 1.6 x 10^-17
Observations of a huge number of binary star systems are consistent with normal elliptical orbits that we can calculate very accurately. This means the light from the approaching and receding stars must be traveling to us at exactly (or almost exactly) the same speed. This is strong experimental evidence that the speed of light is independent of the speed of its source.
Questions about 'speed of light'
A bunch
of very interesting questions come immediately to mind when hearing of
the speed of light speed limit.
Why 3x10^8
m/sec?
Is it
independent of other physics parameters?
Can
it be calculated?
Why
is the speed of light slower in materials?
Why 3x10^8 m/sec?
3 x 10^8 m/sec
is the measured value of the speed of light. There is no (generally accepted)
theoretical reason why it is should be this value, it just is this value.
There are a bunch of constants in physics like this that are measured and
cannot be derived, for example the gravitational constant. A lot of physists
are not too happy about this and for a long time have been working to try
and better understand why these constants take on the values they do.
Is c independent of other physics parameters?
Answer: no. The
speed of light (c) shows up everywhere in fundamental physics equations.
The speed of light (c) is known as a universal constant, as is planck's
constant (h) and the gravitational constant (G). In fact these three universal
constants can be uniqely combined to give fundamental units of time, length,
and mass, known as Plank units, favorites of particle physicists.
planck length
sqrt{hG/c^3}
1.6 x 10^-35 m
planck mass
sqrt{hc/G}
2.2 x 10^-8 kg
planck time (1/c) x planck length
=sqrt{hG/c^5} 5.4 x 10-44 sec
Consider also
(1)
c = 1/sq rt {e0 u0}
(2)
Z0 = u0 x c = sq rt{u0/e0}
(3)
E = m x c^2
(4)
alpha = e^2/(2h x e0 x c)
Equation (1) says that the speed of light can be calculated from two constants of the vacuum: one (e0) is an electric-capacitive scaling constant and the second (u0) is a magnetic-inductive scaling constant. The speed of light is the inverse of their geometric mean.
e0 (electric permittivity) is a constant that scales the electric (E) field
squared
(in a vacuum) to give the energy density stored in the electric field.
Energy density in electric (E) field = 1/2 x e0 x E^2
u0 (magnetic permeability) is a constant that scales the magnetic (H) field
squared
(in a vacuum) to give energy density stored in the magnetic field.
Energy density in magnetic (H) field = 1/2 x u0 x H^2
Equation (2) is a universal constant known as the characteristic impedance of free space (Z0). It is the square root of the ratio of u0 to e0 and has the units of ohms. The value is about 377 ohms and is known very accurately (12 digits). Since ohms in circuit theory are normally volts/amps (and E has units of volt/meter), Z can also be expressed as a ratio of the electric to magnetic fields (E/H) in a vacuum.
Equation (3) is the famous Einstein equation that says the energy and mass are (in some way) equal. c^2 is the (fixed) proportonality constant that scales mass to energy and energy to mass..
Equation (4) is the formula for the fine structure constant, usually designated by alpha. Alpha is a constant of the stamdard model of particle physics (one of 19) that is unusual because it is dimensionless. In quantum electrodynamics the fine structure constant is a coupling constant that indicates the strength of the interaction between electrons and photons. It is also involved in various estimates of the size of the electron. Alpha is equal to the charge of the electron squared divided by 2h (twice plank's constant) x e0 (electric permittivity in a vacuum) x c (speed of light in a vacuum), and its value has been very accurately measured.
Can c be calculated?
Answer: historically,
yes. Maxwell around the time of the US civil war had a eureka moment when
he found in his equations summarizing the laws for electicity and magnetism,
laws based on a huge number of experiments by Faraday & others, that
a self-sustaining electro-magnetic wave was possible. He found he was able
to calculate its speed, and it turned out to be just a combination of two
constant that can be measured in lab experiments with electrcity and magnetism.
When he did the calculation, he found that the speed came out to be 3 x
10^8 m/sec that he knew (even in the 1860's!) was the speed of light. Yikes
(holy shit!), he suddenly realized that light, which had been a
mystery for centuries, was very likely an electromagetic wave (as
Faraday had long suspected).
His equation for the speed of light turned out to be very simple {c = 1/sq rt (eo x u0)}. Speed of light is equal to the inverse of the geometric mean of two constants (e0, u0). One constant (e0) comes from the formula for capacitance (C), where energy is stored in the electric field, and the other constant (u0) comes from the formula from inductance (L), where the energy is stored in the magnetic field. Each constant multiplied by its field squared (E^2 or H^2) yields the energy stored in the field (per unit volume).
A simple (idealized) capacitor is just two plates of area A, separated by distance d. When a voltage is applied between the plates, a (uniform) electric field (E) exists between the plates, and energy is stored in the electric field. A simple inductor is a (circular) toroid of length d, made with N turns of wire, each turn having cross-sectional area A. When a current is flowing through the toroid, a (uniform) magnetic field (H) exists inside the toroid, and energy is stored in the magnetic field.
C = e0 x A/d
L = u0 x N^2 x A/d
or L = u0 x (N/d)^2 x A x d
where
A = area of plates
A = area of each coil in toroid
d = separation of plates
d = length (average circumference) of toroid
N = number of coils in toroid
Energy stored in the electric field of the capacitor = 1/2
e0 x E^2 x A x d
Energy stored in the magnetic field of the inductor = 1/2 u0 x H^2
x A x d
Do you see a symmetry here?
Why is the speed of light slower in materials?
One explanation
I have seen is light slows down in materials because light photons are
constantly being absorbed and reemitted. 'Explanations' like this are useless,
photons in the presence of materials are being absorbed and emitted all
the time.
Speculation on what sets speed of light in vacuum
There
are suggestions and hints that the speed of light (and e0) may be determined
by the properties of the vacuum. In particular, the electric field of light
is slowed down (probably from infinity), because as it travels it has to
continually do (reversible) work polarizing charged virtual particles of
the vacuum (electrons and positrons).
Polarization of vacuum virtual particles could be analogous to the polarization of a dielectric material in a parallel plate capacitor or a cable. Bound electrons in atoms and molecules of the dielectric material are somewhat like little springs. An applied E field does (reversible) work on these bound electrons, slightly displacing them relative to the positive nucleuses, causing the applied E field to be partially canceled. This mechanism increases the stored electric energy, and since it takes time to do work (add energy) dielectrics in cables slow down signal propagation.
Maxwell's equation for a traveling wave require that the energy in the E and H fields remain balanced. When dielectrics increase e, the E amplitude automatically drops such that the electric field (photon) energy does not change, thus keeping the balance between electric and magnetic energy. Therefore u0 is secondary, it's principally eo (or e) that sets the speed of light in a vacuum or in a material..
The suggestions and hints (see below) are all I can find. I can find no value for the bare or naked electron charge. I can find no analysis that says the speed of light is, or is not, affected by virtual particles of the vacuum. What this probably means is the effect of the vacuum on the speed of light and the electron charge is not calculable. Physicists (pretty much) only write up what they can calculate.
Consider:
-- Particle physicists argue that inside a normal electron is a (so
called) 'naked' or 'bare' electron with a higher charge. The argument is
that virtual particles of the vacuum form a cloud around the electron that
is polarized, meaning that in their brief existence positively charged
particles are pulled slightly closer and negatively charged particles pushed
slightly away. Particle physicist Dan Hooper in his 2006 book Dark Cosmos
says this:
During their brief lives the positively charged particles in this quantum sea will be pulled slightly toward the electron, forming a sort of cloud around it. The cloud of positive particles conceals some of the strength of the electron's field, effectively weakening it. (Dark Cosmos, 2006,p 93-94)-- Recent high energy probes of the electron have tended to confirm the virtual particle shielding of the electron E field. The fine structure constant, which is (e^2/h x c), was found to be about 7% higher when part of the virtual shielding cloud was penetrated. This is an increase in q of 3.5 %. Here is an NIST reference:
The virtual positrons are attracted to the original or "bare" electron while the virtual electrons are repelled from it. The bare electron is therefore screened due to this polarization. Since alpha (fine structure constant) is proportional to e2, it is viewed as the square of an effective charge "screened by vacuum polarization and seen from an infinite distance." (NIST, National Institute of Standards and Technology web site)-- About 15 years ago several prominent scientists writing in reputable journals, including the world's most famous journal (Nature), speculated that virtual particles of the vacuum affect the speed of light and suggested this is "worthy of serious investigation by theoretical physicists".At shorter distances corresponding to higher energy probes, the (virtual) screen is partially penetrated and the strength of the electromagnetic interaction increases since the effective charge increases. Indeed, due to e+e- and other vacuum polarization processes, at an energy corresponding to the mass of the W boson (approximately 81 GeV, equivalent to a distance of approximately 2 x 10^-18 m), alpha is approximately 1/128 compared with its zero-energy value of approximately 1/137. Thus the famous number 1/137 is not unique or especially fundamental. (NIST, National Institute of Standards and Technology web site)
The vacuum is not an empty nothing but contains randomly fluctuating electromagnetic fields and virtual electron-positron pairs with an infinite zero-point energy. Light propagating through space interacts with the vacuum fields, and observable properties, including the speed of light, are in part determined by this interaction. ... The suggestion that the value of the speed of light is determined by the structure of the vacuum is worthy of serious investigation by theoretical physicists (S. Barnett, Nature 344 (1990), p.289)Scharnhorst and Barton suggest that a modification of the vacuum can produce a change in its permittivity [and permeability] with a resulting change in the speed of light. The role of virtual particles in determining the permittivity of the vacuum is analogous to that of atoms or molecules in determining the relative permittivity of a dielectric material. The light propagating in the material can be absorbed , but the atoms remain in their excited states for only a very short time before re-emitting the light. This absorption and re-emission is responsible for the refractive index of the material and results in the well-known reduction of the speed of light. (S. Barnett, Nature 344 (1990), p.289), also (later) Barton, K. Scharnhorst, Journal of Physics A: Mathematical and General 26 (1993) p 2037-2046)
Modifications of the vacuum that populate it with real or virtual particles reduces the speed of light photons. (J. I. Latorre, P. Pascual and R. Tarrach, Nuclear Physics B 437 (1995), p.60-82)
As a photon travels through a vacuum, it is thought to interact with these virtual particles, and may be absorbed by them to give rise to a real electron-positron pair. This pair is unstable, and quickly annihilates to produce a photon like the one which was previously absorbed. It was recognized that the time that the photon's energy spends as an electron-positron pair would seem to effectively lower the observed speed of light in a vacuum, as the photon would have temporarily transformed into subluminal particles. (Wikipedia on Scharnhorst)
Fundamental to both approaches is the theoretical picture of the vacuum as a turbulent sea of randomly fluctuating electromagnetic fields and short-lived pairs of electrons and positrons (the antimatter counterparts of electrons) that appear and disappear in a flash. According to quantum electro-dynamics, light propagating through space interacts with these vacuum fields and electron-positron pairs, which influence how rapidly light travels through the vacuum. (comment on a 1990 Barton, K. Scharnhorst paper in Science News, 1990)Mystery of photonsLight in normal empty space is slowed by interactions with the unseen waves or particles with which the quantum vacuum seethes. (Encyclopedia of Astrobiology, Astronomy, & Spaceflight -- David Darling)
John Wheeler, the well known physicist who coined the term 'black hole', said of photons (in reference to single photons that apparently interfere with themselves in double slit experiments) --- A photon is a ''smoky dragon'. It shows it tail (where it originates) and it mouth (where it is detected), but elsewhere there is smoke: "in between we have no right to speak about what is present."
In the well regarded, 1,200 page, 1995, book , Optical Coherence and Quantum Optics by Mandel and Wolf, you find stuff like this:
--- "The one-photon state must be regarded as dstributed over all space-time." (p 480) Well that's sure clear. A photon is everywhere both in space and in time. Yikes!In a generalize way this book derives the time equations of the free E and H fields, and (surprise) it turns out to be exactly Maxwell's field equations.--- "We may regard the corresponding photon as being approximately localized in the form of a wave packet centered at (a known) position at a given time." (p 480) "However, in attempting to localize photons in space we encounter some fundamental difficulties."(p629). So a photon is a wave packet, but it's difficult to locate exactly.
--- "The field (of a photon) is defined in terms of its effect on a test charge, which implies an effect averaged over a finite region of space and time." (p 505). This is the heart of the matter -- What we really know about a photon is how it interacts with an electron (test charge).
--- "The counts registered by a (photo) detector whose surface is normal to the incident field and exposed for some finite time (delta t) are interpreted most naturally as a measurement of the number of photons in a cylindrical volume whose base is the sensitive area of the detector and whose height is c x (detla t)" (p629). In other words a natural interpretation of photons coming into a detector is that they are like rain drops falling to the ground. (This is an analgy that Feynman makes in his introductory video lecture on photons.)
The challenge, which many people have taken up, is to find a picture or model of a photon in space that fits with Maxwell's equations and the experiments underlying quantum physics. Online you can find lots of speculative self-published technical writing about photons.
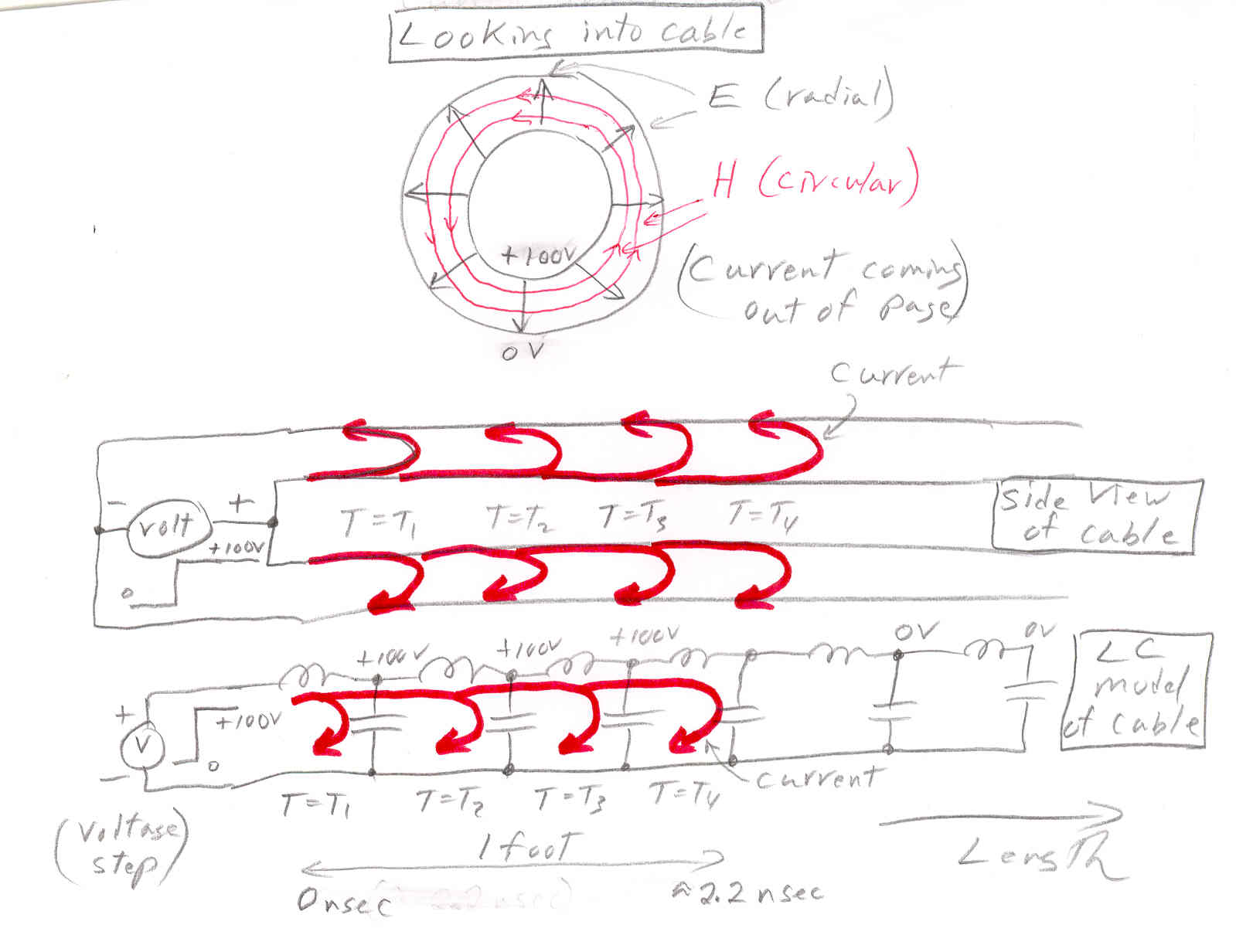
My approach to getting a handle on light photons is to analyze and picture how E and H fields propagate down cables. In real cables signals move a little slower than the speed of light because of the properties of the materials of the cable, mostly the slow down is due to the extra capacitance introduced by the insulating material between the conductors. In an ideal, lossless cable (technically a transmission line or waveguide) the space between the conductors is air (or a vacuum). This allows the signal to propagate at 3 x 10^8 m/sec, the speed of light in a vacuum. Also the conductors are considered ideal with zero resistance.
Are all traveling electromagnetic fields (including those in cables) quantized? How close are cable E and H fields to photons? Who knows. But there does appear to be a lot of similarities in the cable E & H fields and known properties of light:
* fields travel at the same speed (3 x 10^8 m/sec)
* fields are transverse to the direction of motion
* fields are in spacial quadrature (i. e. fields are at right angles to
each other)
* fields are in time phase (i.e. E and H transition at a point in space
at the same time)
But there are differences too. The cable E field picture does not seem to fit with the known polarization of light. Polarization is pictured as the direction light photon E field arrows point. Materials known as polarizers will pass or rotate light with E fields in only one direction (say up). But in a cylindrical cable the propagating E field looks like a ring of arrows point out (or in), like a mixture of all polarization.
One key difficulty with photons is how to picture the E fields. E fields terminate (end) on charges or a conductor. In a cable the E fields is constrained by the geometry of the two conductors. What does the E field look like in space? People wave their arms that the photon geometry must somehow be spherical (or cylindrical). Or they speculate the vacuum throw up some sort of virtual charge cloud that terminates the photon E field.
Another difficulty is what is the meaning of the frequency when applied to the photon 'particle'. No one seems to agree on how long or how many cycles (if any!) a photon has. Quantum mechanics says the energy of the light photon is proportional to its frequency (E = plank's constant x frequency). My thinking on this is shaped by the cable analogy.
In the cable there is no natural frequency or natural sinewave. My analysis of the cable uses an electrical engineer's favorite waveform, the 'step', which is just an instantaneous change in voltage, to drive (excite) the cable. Engineers know this waveform is often more revealing of the properties of a system than the use of sinewaves, which is all the physicist seem to use. In the ideal lossless cable the shape of the voltage (& current) at any point in the cable is exactly the same (except, of course, delayed in time) as the shape voltage (& current) that was applied externally to drive the cable. In other words the cable signal 'frequencies' are determined totally by the source of the signal.
Therefore by analogy with the cable it seems likely to me that the 'frequency' of a photon is determined entirely by the source of the photons. Radio photons, coming from radio antennas, (it seems to me) must have very slowly changing E and H fields (relative to light). Periodically no energy is sent from the antenna and this is why periodically when light E and H fields are plotted they both simultaneously go to zero. At times no (light) energy is in the fields, because no energy was sent.
Signals in a cable as a analog for light in a vacuum
An
electric signal travels down a cable in much the same way light travels
through a vacuum. Studying the details of how a signal propagates in cable
can provide a lot of insight about how light moves both in a vacuum and
in materials. A cable is something you can touch and measure. With a good
oscilloscope you can 'see' how the voltages and currents change as a signal
goes down the cable. It's possible to make circuit models of the cable
that can be analyzed with circuit analysis programs that can can confirm
and extend the test data. Also it's relatively easy to work out the capacitive
(E) and inductive (H) equations of a cable because the geometry is so simple.
Combine these approaches and you can quantitatively and visually
see how a signal moves down a cable, how the E and H fields move. From
there it is but a small step to understanding light in materials..
Studying propagation in a long cable has some nice advantages. One, a cable is a simple geometry with easily measured and calculable electrical parameters inductance (L) and capacitance (C). Two, a cable can be approximated by a repeated simple circuit (series LC) that allows circuit designers (like me) to understand it and calculate the speed using well known circuit design techniques. Three, application of Maxwell's equations to the simple geometry of cylindrical cables is easy, so the speed can be calculated from the electrical parameters of the cable and sketches can be made of how the E and H vectors point as the signal propagates. This approach also is helpful in understanding polarization. The cylindrical geometry of a round cable provides understanding of unpolarized signals, and when extended to an idealized flat cable provides understanding of polarized signals.
Typical cable numbers
As a motor
control engineer, the propagation of electrical signals down cables from
the controller to the motor is something I have often measured and know
something about. Consider a motor connected through a 100 feet cable to
a box of electronics called a motor controller. When the transistors in
the motor controller switch the voltage, which can be very fast (20-50
nsec), there is typically a delay of about 220 nsec before the motor
'knows' the voltage has changed. This 220 nsec delay is the time it takes
the signal at 2.2 nsec/ft to travel down the 100 ft of the cable. (Footnote:
it doesn't matter that the cable might be curled up.) 1 nsec/ft is the
speed of light in a vacuum, so 2.2nsec/ft is about 45% the speed
of light in a vacuum. Signals in a cable travel slower than light in a
vacuum for the same reason that light in glass travels slower.
Measured inductance
and capacitance for a foot of motor cable (consistent with 2.2 nsec/ft)
are typically
L = 50 nh/ft
C = 100 pf/ft
The
delay equation is
delay/unit length = sqrt (LC)
= sqrt (50 x 10^-9 nh/ft) x 0.100 x 10^-9 nf/ft)
= sqrt (5) nsec/ft
= 2.2 nsec/ft
Circuit model of the cable
Inductors
(L) and Capacitors (C) are idealized circuit elements that losslessly store
and release energy. An inductor stores energy in a magnetic (B) field and
a capacitor stores energy in an electric (D) field. Energy stored in an
inductor is proportional to its inductance, and energy storage in a capacitor
is proportional to its capacitance. When you connect an L and C together,
they affect each other in such a manner that energy sloshes back and forth
between them sinusoidally. The time it takes for the energy to slosh from
one to the other is proportional to LC time constant {tau =sq rt (LC)}.
Measured inductance and capacitance for a foot of motor cable are typically (about) L=50 nh and C=100pf. A cascade of a hundred of these 'one foot' LC circuits models a 100 foot cable. The 'one foot' LC time constant (tau), which for series L and parallel C is a delay time, is calculated below and comes out to be 2.2 nsec, a little less than half the speed of light
tau = sq rt (LC) = sq rt (50 nh x 100 pf)
= sq rt (50 x 10^-9 x 100 x 10^-12)
= sq rt (5,000 x 10^-21)
= sq rt (5 x 10^-18)
= 2.2 x 10^-9 sec
(Another characteristic of the cable depends on L.C, its
impedance. Cable impedance (Z) is sq rt (L/C)
Z = sq rt (50nh/0.1nf) = sq rt (500)
= 22 ohms
For this cable electrical signals travel at 45% the speed of light in a vacuum. The time constant (tau) of our one foot LC model turns out to be exactly the time its takes the signal to travel one foot in the cable. A cable with the same magnetic energy storage (L) and four times the electric energy storage (4C) (due to a high capacitance dielectric material between the two conductors) would propagate signals twice as slowly (22.5% speed of light).
Holy shit --- speed of light from static measurements
Note
this interesting fact --- Two statically (nothing moving) measured
cable parameters, inductance, which is proportional to magnetic field energy
storage, and capacitance, which is proprtional to electric field energy
storage, allow us to accurately predict (i.e. to calculate) the speed of
travel of electrical signals down the cable.
It turns out that the same type of prediction can be made for the speed of radiated electromagnetic waves, like light. This was the euraka (holly shit!) moment for Maxwell in the 1860's when he found he could tie electricity/capacitance together with magnetism/inductance in a wave equation, and it yielded a single speed (through a vacuum) for all traveling electromagnetic waves (light, x-rays, etc).
Maxwell wrote in 1864:
This (electromagnetic wave) velocity is so nearly that of light that it seems we have strong reason to conclude that light itself (including radiant heat and other radiations) is an electromagnetic disturbance in the form of waves propagated through the electromagnetic field according to the electromagnetic laws.Precursor to Maxwell -- Faraday rotator (2/11)
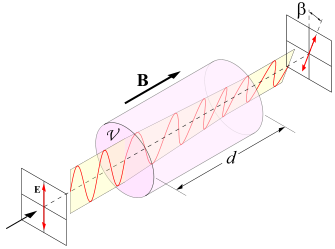
beta angle =( Verdet constant) B d
(transparent) material effect
source -- Wikipedia 'Faraday effect'
The Faraday effect (or Faraday rotator) is a rotation of the angle of linearly polarized light caused by a an axial DC magnetic field in the path. The degree of rotation depends on the strength (& polarity) of the B field and the length of the path. Looks like this is only(?) a material effect, but it happens too in outer space caused by free electrons. Frankly I don't have a clue as to how to think about this (well see below).
Here's a thoughtThe non-mathematical explanation given in Wikipedia is that linear polarized light can be thought of as two counter rotating circular polarizations and that the DC magnetic field changes the speed of rotation (refractive index) of the two of them differently causing a shift in the linear polarization angle.
Elsewhere in this essay by analogy with light travel in a cable I argue you can think of light slowing down in a material as being due to a 'capacitance' increase, or more energy (and time) needed for the E field to move the electrons of the atoms of the material. If the slightly moving electrons are thought of as a 'current', then by the right hand rule (I cross B) a rotational force is exerted on the moving electrona in such a way that it might very well speed up a circularly polarized E field going one way and retard a circularly polarized E field going the other way.
Still the important point historically is in 1845 Faraday knows a magnetic field can change light, so clearly they interact, and it does suggest that maybe they interact because light itself is electromagnetic.
Speed of light from static forces
Meters that
measure capacitance and inductance have a system of units built into them,
such that capacitance is read in uf and inductance in uh. When the speed
of light is derived from measurements made with capacitance and inductance
meters, it is not immediately obvious what role the scale factors built
into the meters play. There is another way to statically measure
the speed of light that makes it clear that units don't matter.
Here's the equation for the force between charges (q1 and q2) separated by r (coulomb's law), and the equation for the force (per unit length) between parallel wires (carrying currents I1 and I2) separated by r. Since c = sqrt(1/e0 u0), we can replace u0 in the equation with (1/e0 c^2).
Force = k x q1q2/r^2
where k = 1/(4 pi e0)
Force/(unit length) = k x I1I2/r
where k = u0/(2 pi) = 1/(2 pi e0 c^2)
From above you can see that the speed of light can be determined from the ratio of measured electric and magnetic forces, e0 drops out. As Feynman points out, this measurement of c is also not dependent on the definition of charge. If q were to double, then both forces quadruple (current doubles because it is charge flow per sec), so the ratio is unaffected. Units of distance (r) don't matter either because the measurements can be made at the same distance or at ratioed distances.
Interpreting the LC slow down
Here is a
physical interpretation. Inductance slows down the rise of current as energy
flows into the magnetic field around the wires. Capacitance (transiently)
pulls or steals current out of the wire to build up the electric field
in the insulator between the wires as the voltage rises. (See section of
Displacment current.) Both mechanisms, the retarding of current and
diversion of current, slow down the propagation of the signal down the
cable.
Light slows down in transparent materials for the same
reason
Very likely
the reason for the slow down of light in transparent materials is the same
as in the cable. It is due to the need to repeatedly pump energy into and
out of the materials magnetic and electric fields. In fact by analogy with
the cable I predict (I do not know as I write this) that the speed of light
in transparent materials will be proportional to 1/sq rt (e x u) , where
e is the ratio increase in eo (electric constant) in materials and u is
the ratio increase in uo (magnetic constant) in materials.
Yup, here are the formulas for index
of refraction as a function of the electric and magnetic parameters of
the material. The speed of light in materials is the speed of light in
a vacuum (c) divided by the index of refraction (n).
speed of lignt in materials = c/n.
The index of refraction is given in terms of the relative electric permittivity (er) and relative magnetic permeability (ur). (ke is called dielectric constant and km is called the relative permeability.
n = sq rt (er x ur)
er= ke x e0,
ur=km x u0
e0 = 8.8542 x 10^-12 F/m u0 = 4 pi
x 10^-7 H/m
LC ladder model for light entering a material
The LC ladder
model of a cable can be extended to (I think) shed some light on details
of what happens when light goes from a vacuum into a transparent material.
Light travels more slowing in materials because the electrons in the material
raise the e (electrical permittivity) higher than the vacuum. In the sketch
below the transition of light going from vacuum into a transparent material
is modeled by increasing the capacitance (C) by four.
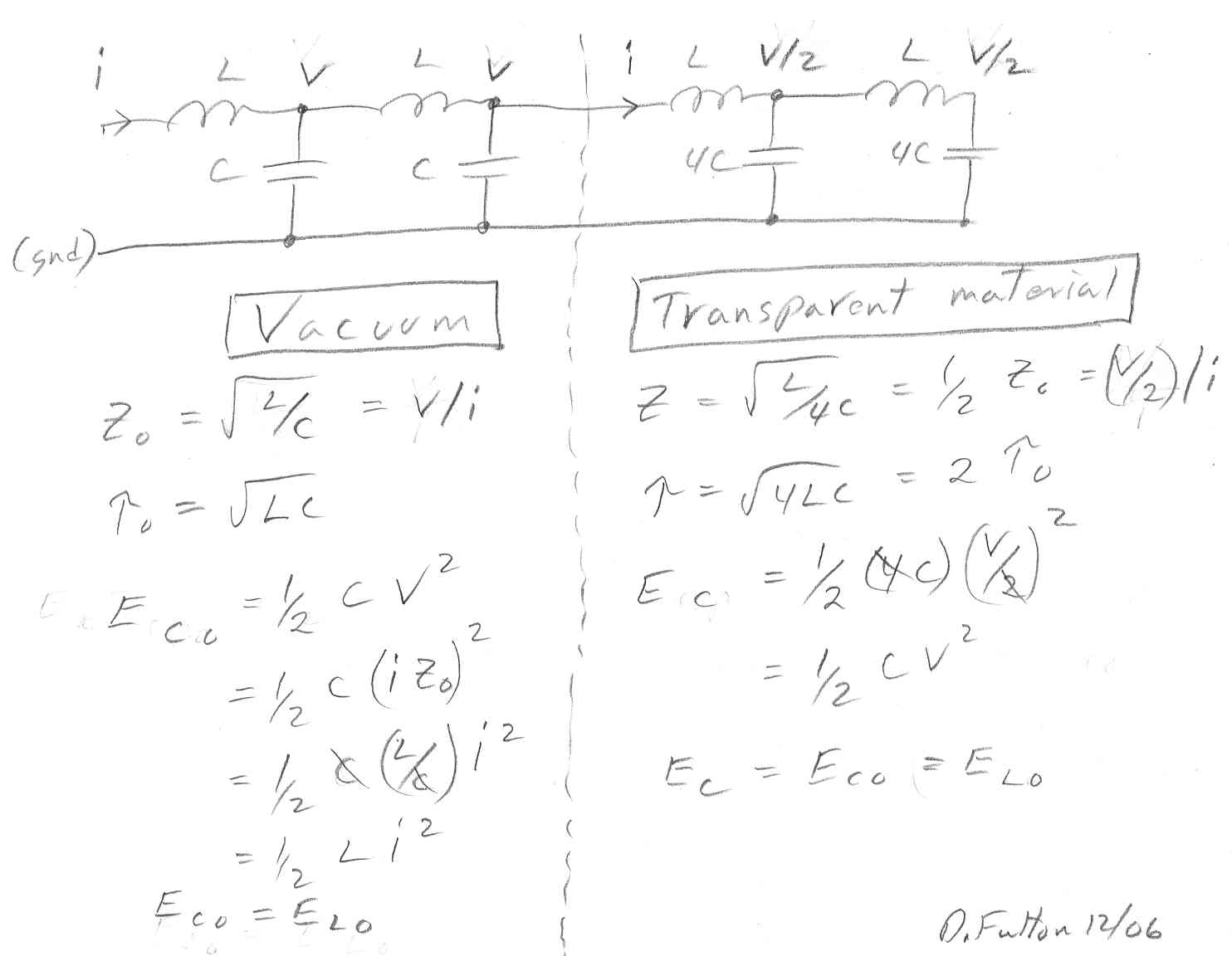
As the sketch shows four times higher capacitance doubles the time constant per unit length (sqrt{LC}) and also lowers the impedance (Z = sqrt{L/C}) by two. A doubled LC time constant means it takes twice the time to travel the per unit LC length, in other words the speed of light has been cut in half. A key point to note is that the energy in the capacitor across the transition remains unchanged, and it stays equal to the energy in the inductor. When the capacitance increases by x4, it causes Z to drop in half which causes the voltage to drop in half. The result is that capacitor energy (1/2 x C x V^2) is unchanged, the lower voltage compensating for the increased capacitance.
The LC ladder parameters are translated into the field equivalents for light below:
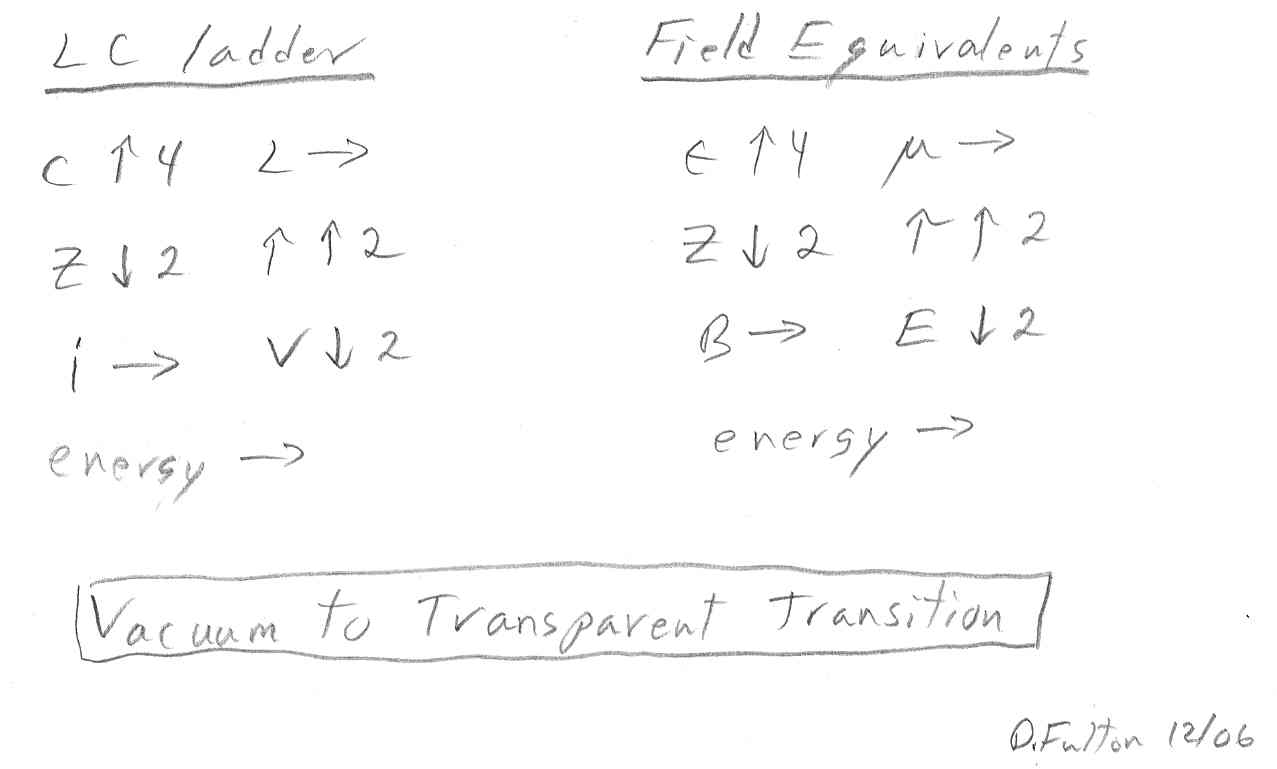
In summary the LC ladder model is telling us (predicts) that when light enters a material from a vacuum it slows down due to the higher permittivity. At the field level the E field drops because the impedance of the material is lower than the vacuum with H (and B) in the material the same as in the vacuum. The drop in E just compensates for the increase in permittivity keeping the E field energy unchanged and the same as the H field energy. The energy balance between electric and magnetic fields, which is a requirement for propagation of the wave, is maintained.
Another (interesting/curious) result of this analysis is that the (semi-classical) 'size' of a photon in a material is the same as in vacuum. The energy stored in the electric field is the electrical energy density (1/2 x e x E^2) intergrated over the volume of the field. Since E is down by two when e is up by four, it must mean the field volume, i.e. the spacial extent of the photon E field, is the same in material as in vacuum!
Capacitor with a dilectric material in the gap
The classic
textbook capacitor is two parallel plates (close together) with air between.
Inserting a dielectric, insulating material in the gap can increase the
capacitance x3-4, so almost all practical capacitors use dielectrics
in the gap. A dielectric increases the electric permittivity (e = ke x
e0) of the capacitor by making ke > 1. A higher electric permittivity and
higher capacitance means more energy is stored in a capacitor for a particular
voltage. The circuit formula for energy storage in a capacitor is the first
formula below. The energy in a capacitor is all stored in the electric
field, so the capacitor energy formula can also be written in terms of
the electric field density and volume of the gap..
E=1/2 x C x V^2
E=1/2 x ke x e0 x E^2 x (volume in gap)
The relationship in a capacitor between charge, voltage and capacitance is q = CV, which can be written
C = q/V = ke x e0 x (area of plates)/(gap between plates)
So when a material is inserted in the gap, the capacitance (C) goes up, charge on the plates (q) goes up, but for a specific voltage (V) the (net) E field (volt/m) in the gap of the capacitor is unchanged. The reason the charge on the plates (q) can go up without the (net) E field in the gap going up is because a partially cancelling E field is formed by electrons in the material as their (dipole) orientation (or charge displacement) is affected by the external E field.
Link below has a little sketch showing charge on a capacitor plates and its dielectric. It's text says:
"The electric field causes some fraction of the dipoles in the material to orient themselves along the E-field as opposed to the usual random orientation. This, effectively, appears as if negative charge is lined up against the positive plate, and positve charge against the negative plate."http://www.pa.msu.edu/courses/2000spring/PHY232/lectures/capacitors/twoplates.html
Question --- The above text makes it sound like capacitor dielectrics have pre-existing (bulk) domains, like a ferromagnet, that are reoriented by the applied E field. Is this true, or does the dipole reorientation occur at the level of individual atoms or molecules?
How material increases capacitance
A key question is
how, at the atomic or molecular level, does running the E field through
a material increase the energy stored in the capacitor. Normally in an
atom (or molecule) the positive charge of the nucleus is completely balanced
by the surrounding electron cloud. It must be (it seems to me) that the
E field, which pushes on positive charge and pulls on negative charge,
must (in some sense) 'separate' the opposite charges of all the dialectic
atoms (or molecules). In practice this probably means all the electron
clouds move a little. It takes work (and time) to separate the charges
so this is where the extra energy goes when the capacitor is charged. This
is reversible operation. The energy is returned when the charges return
to their normal equilibrium positions.
If what is
happening is reorientation (rotating) the dipoles of molecules, I think
the same argument applies about the work required and it being reversible.
This picture of partial cancellation in an electron's external E field seems a lot like the partial cancellation of the E field in a capacitor with a dielectric material! In both cases the applied E field is doing work to separate (move) a matrix of positive and negative charges. Light slows down (from infinity?) in a vacuum because the E field has to do work on the virtual particle charges as it propagates. It's seems directly analagous with the added slow down of light moving in a material due to the fact that it has to move more charge.
Is this not the explanation of where e0 (electric permittivity) of the vacuum, or alternately the capacitance of the vacuum, comes from? I bet it's directly calculable from the vacuum properties.
Do vacuum properties set the speed of light?
--
(from my email to Ken Bigelow 1/07)
Ken
Have you ever
looked into why the speed of light is 3 x 10^8 m/sec?
Quantum physics says the vacuum is full of virtual charged particles. Particle physicists argue the measured charge of the electron is lower than the so-called 'naked' or 'bare' electron because the electron is always surrounded by a cloud of virtual particles (Ref: 2006 book Dark Cosmos by particle physicist Dan Hooper). The charge is lowered because the virtual cloud is polarized, the E field of the electron pulling the + charges closer and pushing the negative charges away. There is data to support this view. Probes of the electron at high energy measure the fine structure constant (e^2/(c x h) higher by 7% (Ref: NIST). The interpretation is that the probe particles are partially penetrating the virtual cloud around the electron.
The polarization of virtual vacuum particles certainly seems a lot like the polarization of charged particles in dielectrics, which increase capacitance and slow down light in materials. So is the speed of light set by virtual vacuum particles, more specifically by the need to do reversible work on them as light propagates? It's an interesting speculation. I found a reference in the journal Nature about 16 years ago that advised particle physicists to seriously consider this idea.
Have
you looked into this? I can find little more. My guess is that it's
not calculable. Physicists tend to talk about only what they can calculate.
Don
*** In Oct 2007 nearly nine months after I wrote above, I found this recent apparent confirmation from a reputable source --- 2007 lecture notes from Univ of Ill physics course on electromagnetism. Note this appears to be presented as fact to students, not as speculation.
Key quote --- "The macroscopic, time-averaged electric permittivity of free space (e0 = 8.85 10^-12 F/m) is a direct consequence of the existence of these virtual particle antiparticle pairs at the microscopic level."
http://online.physics.uiuc.edu/courses/phys435/fall07/Lecture_Notes/P435_Lect_01_QA.pdf
"What is the physics origin of the 1/e0 dependence of Coulomb’s force law?
At the microscopic level, virtual photons exchanged between two electrically charged particles propagate through the vacuum – seemingly empty space. However, at the microscopic level, the vacuum is not empty – it is a very busy/frenetic environment – seething with virtual particle-antiparticle pairs that flit in and out of existence – many of these virtual particle-antiparticle pairs are electrically charged, such as virtual e+ e- , and muon+ muon-, tau+ tau- pairs {heavier cousins of the electron}, 6 types of quark-antiquark pairs qq and also W- W+ pairs (the electrically-charged W bosons are one of two mediators of the weak interaction), as allowed by the Heisenberg uncertainty principle (delta E delta t) > h bar. The macroscopic, time-averaged electric permittivity of free space (e0 = 8.85 10^-12 F/m) is a direct consequence of the existence of these virtual particle antiparticle pairs at the microscopic level." (from Univ of Ill physics link above)
Consider the following facts about e0, vacuum, and
speed of light
Undisputed
------------------------------
(all this is from a Barry Setterfield oddball paper,
25 pages, 87 references, 2002, about zero point energy)
(age 64 religious guy, creationist cosmologist!)
http://www.journaloftheoretics.com/Links/Papers/Setterfield.pdf
Really important to vet these references
from Setterfield
1 S.M. Barnett: Quantum electrodynamics - Photons faster than
light?; Nature 344, No. 6264 (1990) p 289
2 G. Barton: Faster-than-c light between parallel mirrors.
The Scharnhorst effect rederived; Physics Letters B, 237(1990) p 559-562.
3 K. Scharnhorst, Phys Lett.
B. 236 (1990), p.354.
3 G. Barton, K. Scharnhorst: QED between parallel mirrors: Light signals
faster than c, or amplified by the vacuum; Journal of Physics A: Mathematical
and General 26(1993)2037-2046.(Scharnhorst effect consists of the variation
of the speed of the light when this is submitted the confined spaces.)
4 J.I. Latorre, P. Pascual, R. Tarrach: Speed of
light in non-trivial vacua; Nuclear Physics B p 437(1995) .
useful Wikipedia on Scharnhorst (in Italian), but with English references
http://en.wikipedia.org/wiki/Scharnhorst_effect (english, no references)
------------------------------------------
stuff on interaction of electrons in orbit with vacuum
from same Setterfield paper
-- A paper published
in May 1987 shows how the problem may be resolved69. The Abstract summarizes:
“the
ground state of the hydrogen atom can be precisely defined as resulting
from a dynamic equilibrium between radiation emitted due to acceleration
of the electron in its ground state orbit and radiation absorbed from the
zero-point fluctuations of the background vacuum electromagnetic field…”
In other words, the electron can be considered as continually radiating
away its energy, but simultaneously absorbing a compensating amount of
energy from the ZPE sea in which the atom is immersed. 69 69. H. E. Puthoff,
Physical Review D, 35 (1987), p.3266.
70. T. H. Boyer, Phys. Rev. D 11 (1975), p.790
71. P. Claverie and S. Diner, in Localization and
delocalization in quantum chemistry,
Vol. II, p.395, O. Chalvet et al., eds, Reidel, Dorchrecht,
1976.
-- This
development was considered sufficiently important for New Scientist to
devote two articles to the topic72-73. The first of these was entitled
“Why atoms don’t collapse.” 72. Science Editor, New Scientist, July 1987.
73. H. E. Puthoff, New Scientist, 28 July 1990. pp.36-39.
----------------------------------------
above are Tid bits from peer review journals or reputable
sources
Conclusions (early 2007)
-- (as fas
as I can find out) the charge of 'bare' or 'naked' electron has never been
calculated.
-- (as fas
as I can find out) the speed of light in a vacuum has never been calculated
from the properties of a vacuum.
-- It seems
very likely (to me) that permittivity (e0) of the vacuum is caused by virtual
charge being polarized and that this mechanism is basically the same as
increase in permittivity caused by the polarized charges in dielectric
materials.
-- It seems
very likely (to me) that permittivity (e0) of the vacuum is caused by virtual
charge beeing polarized. is very similiar to the increase in permittivity
hrtr.
There is another
interesting possibility for breaking the light-barrier by an extension
of the Casimir effect. Light in normal empty space is " slowed"
by interactions with the unseen waves or particles with which the quantum
vacuum seethes. But within the energy-depleted region of a Casimir
cavity, light should travel slightly faster because there are fewer obstacles.
A few years ago, K. Scharnhorst of the Alexander von Humboldt University
in Berlin published calculations4 showing that, under the right conditions,
light can be induced to break the usual light-speed barrier. (Encyclopedia
of Astrobiology, Astronomy, & Spaceflight -- David Darling)
Scharnhorst,
K. Physics Letters B236: 354 (1990).
In 2002, physicists
Alain Haché and Louis Poirier made history by sending pulses at
a group velocity of three times light speed over a long distance for the
first time, transmitted through a 120-metre cable made from a coaxial photonic
crystal.[1]^
Electrical pulses break light speed record, physicsweb,
22 January 2002; see also A Haché and L Poirier (2002), Appl. Phys.
Lett. v.80 p.518.
(very interesting) classic oddball paper
http://www.ldolphin.org/setterfield/redshift.html
Is this what sets the speed of light?
(this section
is I write as pure speculation in early 2007 --- I have seen no references
on this as I write)
We know the speed of light is determined (only) by the vacuum parameters e0 and u0 {c = 1/sqrt(e0 x u0)} If there is a virtual particle cloud explanation for u0 comparable to the explanation for e0 (and I bet there is), then cannot e0 & u0, and hence the speed of light, be calculated from plank virtual properties of the vacuum.
In other words have we not (in a sense) figured out why the speed of light in a vacuum is 3 x 10^8 m/sec?
Does not light slow in materials for the same reason?
(see above
for Univ of Ill material)
So is this
not also the explanation of why (at the atomic level) light travels slower
in materials? It takes extra time (assuming power is not infinite)
for the E field to move the electron clouds in the atoms (or molecules)
of the material over and then back as the light wave pass?
Note, above seems to me a much more straightforward (classical/circuit) explanation for the slow down of light than an 'explanation' I sometime see from physics types. They sometimes say the slow down of light is due to photons being absorbed and then remitted by the atoms of the material. However, physics types seem to assume that photon absorption and remission in many other cases, like mirrors, occurs instantaneously. Or is there really a delay with real mirrors, and it's just that most discussions assume ideal mirrors, in the same way an electrical engineer often assumes ideal, lossless conductors?
Deriving the equation of signal velocity in a
cable
Consider an
(idealized) cable that consists of two (metal) cylinders one inside the
other. The two cylinders act like the two wires in lamp cord, meaning the
current that travels down one cylinder returns via the other cylinder.
To keep the equations very simple we assume the inside and outside cylinder
are close to the same size with only a small gap between them. With this
assumption we can treat the the gap between cyclinders like it's an ideal
parallel plate capacitor (just bent around) with a uniform E field across
the gap.
Assign
h = small segment length of a long cable (say 1 ft)
r = radius (to center of gap)
d = gap (between cylinders)
From circuit analysis of LC model of the cable we know the speed it takes for a signal to go (say) 1 ft down a cable is just the time constant of the circuit model for 1 ft, which is tau = sq rt {LC}. Generalizing to cable segment length (h) the velocity of travel down the cable is
vel = distance/time = l/sq rt (LC)
where
L = inductance for length h
C = capacitance for length h
The E (or D) field is all between the cyclinders, and
it's direction is radial, arrows pointing from one cylinder to the other
cylinder. Equation for an ideal parallel plate capacitor is C = e x A/d.
To get the area we just unwrap (lengthwise) 1 ft of the cable to make a
parallel plate capacitor with area (2 pi r) and gap (d).
C = e x area/d
C = e x (2 pi r) x h/d
or = e x h x (2 pi r)/d
The H (or B) field is all between the cyclinders,
and looking at the cable end on it's direction is circular, arrows wrapping
around the axis of the cable. The general equation of inductance is L x
i = N x flux. Here N =1 and flux is (u x H) x area. If we cut open lengthwise
a cable segment, we can see the flux (H or B) flows is the area (h x d)
formed by cable segment length (h) and gap between cylinders (d).
L = flux/i
= u x H x area/i
= u x H x (h x d)/i
From Maxwell's equation we use Ampere's law (H x length
= N x i) where the path follows H (or B) around the cylinders. The (average)
radius is (r) so the path length is (2 pi r) and (H x length = N x i) simplifies
to
H x (2 pi r) = i
H = i/(2 pi r)
Substituring H into the equation for L we get
L = u x H x (h x d)/i
= (u x h x d /i) x i/(2 pi r)
L = u x h x d/(2 pi r)
Finally the velocity of a signal down the cable is just
length of cable segment (h) divided by the propagation time for the segment
tau = sq rt {LC}, where L and C are the inductance and capacitance per
length segment (h) of the cable
velocity = distance/time = h/sq rt {LC}
= h/sq rt {u x h x [d/(2 pi r)] x e x h x (2 pi r)/d}
= h/sq rt {u x e x h^2}
= h/ h x sq rt {u x e}
= 1/ sq rt {u x e}
Note the equation we have calculated for the speed of travel of electrical signals down a cable is exactly the same as the general equation for the speed of of light in materials!
velocity = 1/sq rt {e x u}
(in cable and materials)
c = 1/sq rt {e0 x u0} (in vacuum)
Calculating energy in E and H fields
First we need
to calculate the impedance (Z = ratio of volt/amp) of the cable. Interestingly
the impedance of cables like this (technically known as transmission
lines) even though composed of reactive elements (L,C) is in real ohms,
just like a resistor.
Z = v/i = sq rt (Z^2) = sq rt (Lw/Cw)
= sq rt{(u x h x d/(2 pi r}/ e x (2 pi r) x h/d
= sq rt{(u x x d^2)/(2 pi r)^2 e )}
= d/(2 pi r)sq rt (u/e)
Note Z of free space is known to be
Z free space = sq rt (u0/e0)
= sq rt (4 pi x 10^-7/8.8 x 10^-12)
= 377 ohms
The cable Z came out to be {d/(2 pi r) x sq rt (u/e). This is just Z (in materials) scaled by the geometric constraints of the cable on the length of the E and H vectors, specifically the ratio of the length of the E vector (d) to the length of the H vector (2 pi r) . What this means (almost for sure) is that the E and H fields of light in free space are the same size (E and H vectors are the same length).
Energy in the
electic field = 1/2 x C v^2 = 1/2 x e x E^2 x volume
= 1/2 x {e x (2 pi r) x h/d} x v^2
Energy in the
magnetic field = 1/2 x L i^2 = 1/2 x u x H^2 x volume
= 1/2 x {u x h x d/(2 pi r)} x i^2
substituting v = i x Z in the electric energy formula
= 1/2 x {e x (2 pi r) x h/d} x v^2 (electric energy)
= 1/2 x {e x (2 pi r) x h/d} x i^2 x (d/(2 pi r))^2 x (u/e)
= 1/2 x {h} x i^2 x (d/(2 pi r)) x (u)
= 1/2 x {u x h x d/(2 pi r)} x i^2 (magnetic energy)
hence half the total energy is stored in the electric field and half in the magnetic field
How E and H fields 'fly' down a cable
Seems
to me a good starting point to understand how light travels in space is
to understand (in detail) how voltage transitions (steps & ramps) travel
down cables. It's not too much of a stretch to picture a light beam in
space as having fields (something) like those in a cable, in other words
thinking of light as traveling in an invisible (straight) cable, or light
pipe, in space. Light is known to be a transverse wave, meaning the
E and H fields point at right angles to the direction of travel, and the
E and H fields are at right angles to each other too. This is how the fields
in the cable point. The E field points radially out (or in) and the H field
goes around the cable.
Of course, E and H fields of light (photons) in space don't have conductors limiting the extent of their fields spacially, so light photons must (in some way) have a spacial field limit based on their energy, which (I think) is equivalent to saying based on the time rate of change of the source and of the fields at a specific point in space.
The cylinderical geometry of the fields is, of course, forced by the geometry of the conductors of the cable. The common solutions of Maxwell's equations for light in free space are a linear polarized and circularly polarized waveforms. (I have read that there is also a cylindrical solution, but I have not found it.) Each local region of the cable, however, does appears to be a good analog for linearly polarized light in free space, because the the E and H fields in a local region are fixed in orientaion, crossed, and transverse to the direction of travel.
Another issue is the how the E and H fields are synchronized in time. The field equations of light show the E and H are in time phase, meaning they increase (and decrease) at the same time. When I look at the phase relationship in the LC ladder model of a cable I don't get a simple answer. The voltage across each capacitor is the local E field, that's clear. However, the two inductors that connect to each capacitor have different currents (with different phases) in them, so which inductor current sets the local H field? Here is some detail:
The H field (via right hand rule) depends on the current in the segment. Spice simulation shows the current divides and flows in two or more caps at the same time, so there must be higher current in the local segment inductor than in the cap. The cable load on each segment looks resistive (Z = sq rt (L/C)) (known to be the case in transmission lines and confirmed by simulation), so the the current in the local segment inductor has two components. One is the current in the segment cap, which is proportional to the derivative of the voltage (i = C dv/dt). The other component is the load current into the rest of the cable, which is in-phase with the voltage (i = v/Z = v/sq rt (LC))). The load current, of course, is the current flowing in the inductor of the next segment inductor.
The E field is the segment capacitor voltage divided by the distance (E =v/d). The E field and H field, as defined by the current in the next segment, are both in-phase because they are both in phase with the segment voltage. However, the current in this segment's inductor also includes the local capacitor current, so it differs (somewhat ) in phase and magnitude from the next segment inductor, hence the ambiguity.** I think I see how to resolve the ambiguity. The ladder can be made finer and finer by taking the capacitance and inductance per ft, then per inch, then per mil, etc. As resolution gets finer, L and C both get smaller (in proportion) with the ratio of L/C staying constant. The difference current in the two adjacent segment inductors is just the current in the capacitor, but as the ladder gets finer the impedance of each cap goes up (Z cap = 1 / C x pi freq) so the capacitor current goes down. The current in the next segment inductor (v/sq rt (L/C)) is unchanged because the ratio of L to C is unchanged. So in the limit of a fine resolution ladder the current in a segment inductor approaches the current in the next segment inductor. The ambiguity vanishes.
Conclusion --- LC model of a cable shows the E field (capacitor voltage) and H field (inductor currents) are in phase.
My sketches below show the details of a voltage step (0V to 100V instantaneous) flying down a cable (at about 1/2 the speed of light). For a step of 100V as shown the E field (radial) and H field (circular) in the cable after the edge flys by is totally static. In other words there is (effectively) no frequency here. This is a quasi-static case.
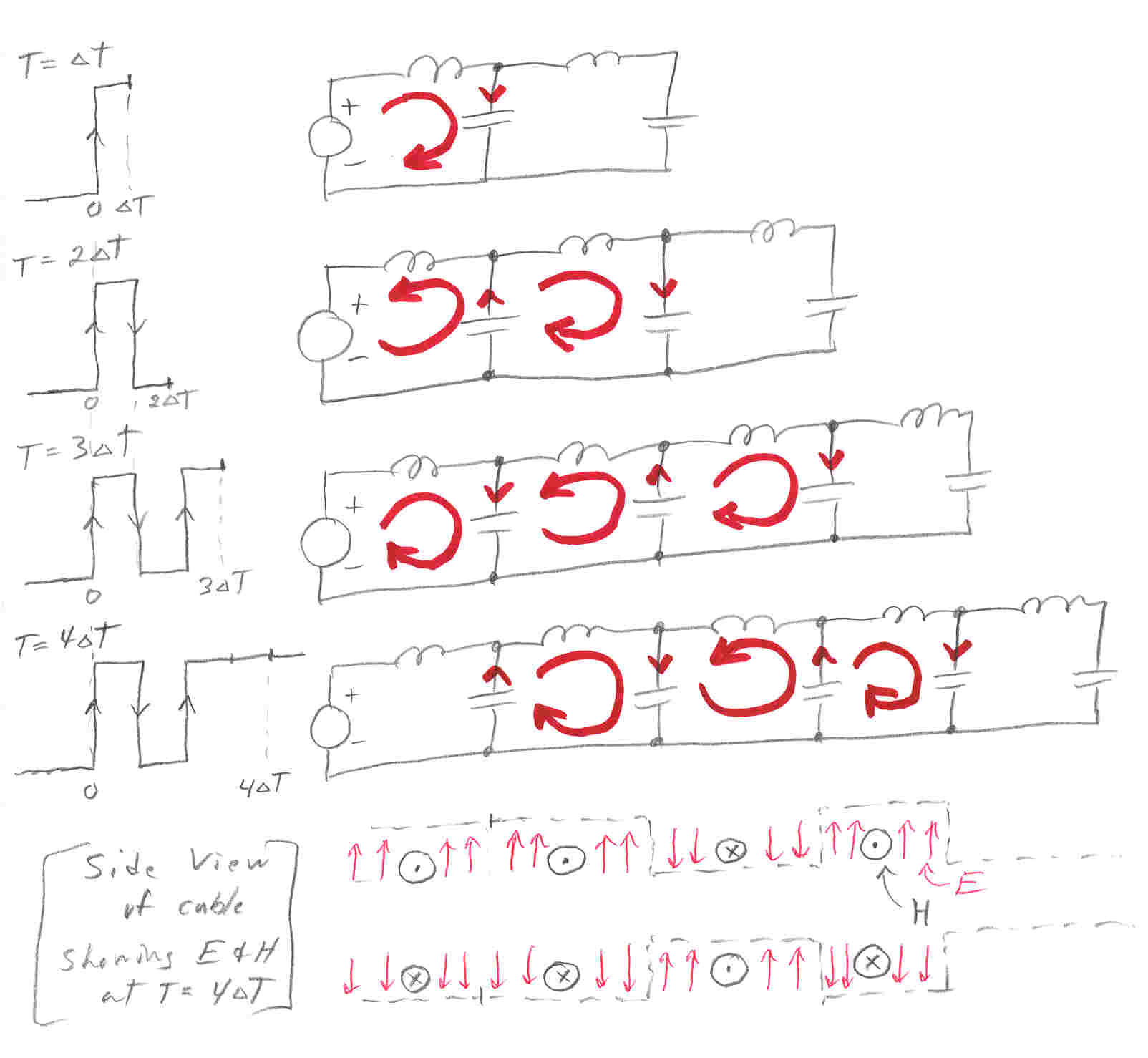
Below shows a burst (three transitions) propagating down a cable. Note the currents in the LC ladder and directions of the E and H fields reverse at each transition. I don't think there is any frequency limit (in principle) for an ideal lossless cable. So if 'delta t' =6.66 x 10^-16 sec, which is half the period of a cycle of blue light, is this (like) the cable analog of a blue light photon?
Feynman's simple model of radiation
In
Feynman's famous books Lectures on Physics (Vol II, pages 18-5 to
18-9) he shows how to generate a single rectangular pulse of radiation.
This is done by starting with two, superimposed, infinite planes of charge
(one positive, one negative) that are not moving. Initially there is no
E or H anywhere outside the planes. One plane is them moved (downward)
a little at constant speed and then stopped. Current, being the rate of
change of charge, steps up from zero to a constant value (positive) while
the charge is moving and then steps back to zero when the charge stops
moving.
Feynman shows that a thin plane of spacial quadrature, time in-phase, E,H radiation fields fly out at velocity c. E points opposite the direction of the motion and H is in quadrature such that (E cross H), the poynting vector, points in the direction of propagation. These fields have no sinewaves, E and H simultaneously step up to a fixed value and then back to zero. He shows this solution is compatible with Maxwell's equations by drawing two rectangular loops in spacial quadrature at the leading boundary of the fields and applying the two Maxwell line integral equations (see below). Since the loops do not include the plane, there is no current through the loops, so J=0.
Line integral of E ds = - d/dt (flux of B thru loop)
c^2 x Line integral of B ds = J/e0 + d/dt (flux of E thru loop)
Feynman's text here says --- The fields have 'taken off, they are propagating freely through space, no longer connected in any way with the source. .. How can this bundle of electric and magnetic fields maintain itself? The answer is by the combined effects of the Faraday's law (#1 above) and the new term of Maxwell (#2 above). ... They maintain themselves in a kind of a dance, one making the other, the second making the first, propagating onward through space.Notice the language "one making the other, the second making the first" is a little vague about the time sequence. Do the fields create each other sequentially or simultaneously? Maybe for times set by uncertainty principle (plank constant divided by energy) it can be said that the fields make each other in turn, but from the analysis it seems fair to say that the changing E and B are simultaneously creating each other.
More on Feynman's model -- another proof E and H are
in time phase --(my email to Ken Bigelow 1/07)
Ken
I was looking at my Feynman Lectures on Physics (Vol II, 18-4) and found
he introduces radiated electromagnetic fields with a very simple example.
The source is contrived (a superimposed infinite sheet of +charge and –charge,
one of which he moves a little at a constant speed and then stops), but
the beauty of this example is that the the radiated fields that fly off
the charge planes are very simple. As the field 'pulse' passes a point
in space, the E and H step up from zero to a fixed value and then back
down to zero again. He draws two rectangular loops in spacial quadrature
at the leading edge of the fields and shows that you can calculate E and
H (almost by inspection) and that this result satisfies Maxwell's integral
equations.
In Feynman's example there are no sinewaves, just two steps, so there is no way E and H can be in time quadrature. The traveling “little piece of field” (Feynman's words) is the superposition of two field steps created when the charge sheet starts and stops moving. Application of Maxwell's equations seems to show E and H are simultaneously creating each other. Feynman in his text is a little vague about exactly how the fields create each other, saying “by a perpetual interplay – by swishing back and forth from one field the other – they must go on forever ... They maintain themselves in a kind of a dance -- one making the other, the second making the first --- propagating onward through space.” (Maybe it could be argued they sequentially create each other down near plank time by application of the uncertainty principle.)
The same analysis can be applied, with the same result (E and H step simultaneously),
to local regions of the ideal cylindrical cable that I have been studying.
Don
Applying Feynman's analysis applied to the cable
Feynman's analysis
can be applied to show the spacial quadrature, time in-phase fields inside
an ideal cable are consistent with Maxwell's equations. Since the amplitude
of the fields is constant, the changing flux within the loops is just the
new flux added in time (delta t) as the fields propagate. The right side
of the loop is in the volume where the fields have not yet reached, so
only the left vertical leg of each rectangular loop has a non-zero value.
The analysis shows that the fields generated by d/dt of the other field's flux are only consistent, and compatible with sustained propagation, when the (velocity of propagation) = c. The analysis also shows that the magnetic field is (always) equal to the electric field divided by the speed of light (B=E/c).
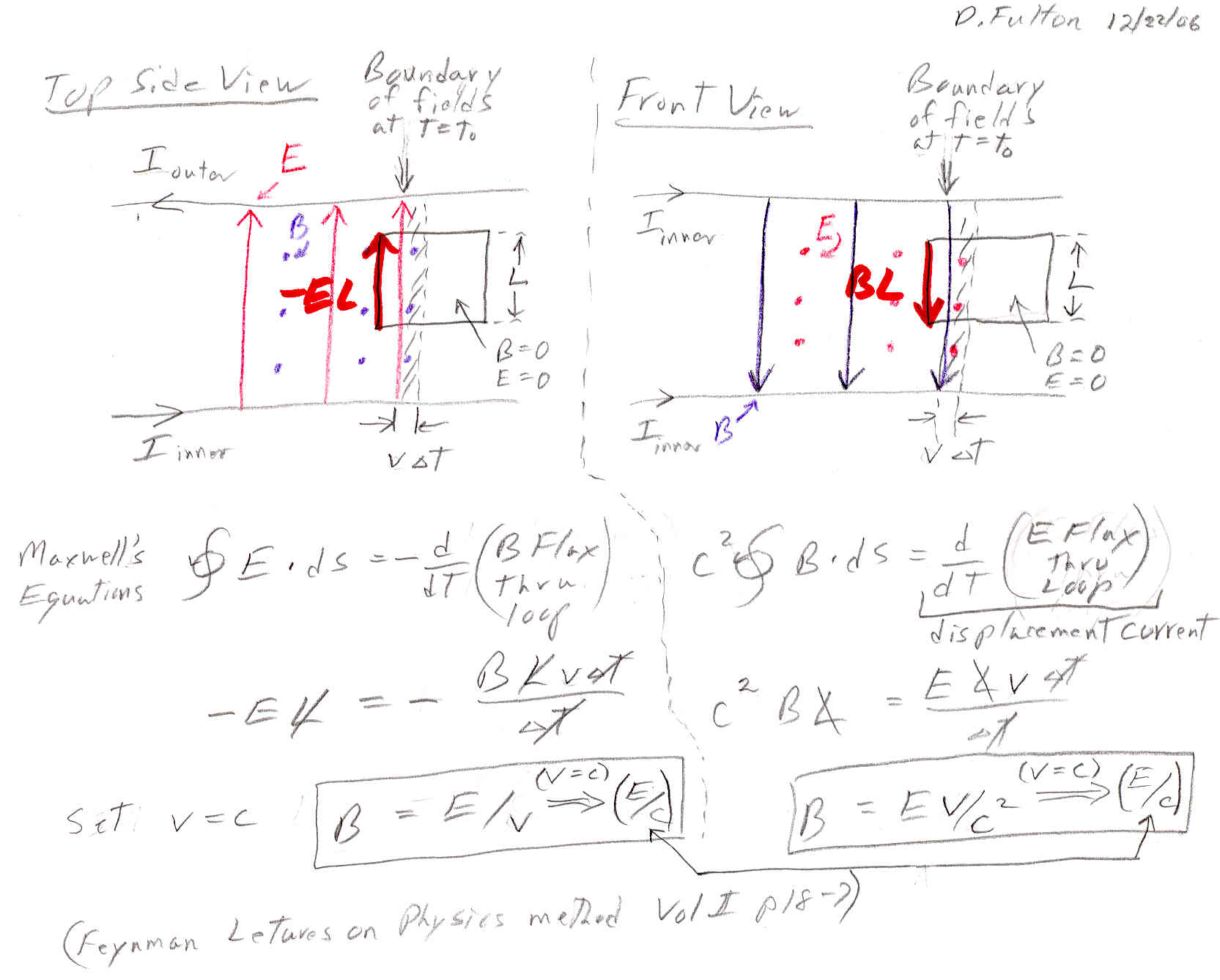
The criteria that (B=E/c) means that energy stored in the magnetic field (in both radiated fields and the cable fields) is equal to the energy stored in the electric field (see below).

Drawing a fundamental conclusion about what sets the
speed of light
We have seen
above that when Maxwell's equations are written using c rather than u0,
B and u0 come out to be secondary. Maxwell's equations force the value
of B to be slaved to E such that the energy stored in both fields
is equal. If propagation is in a material such that capacitance and e are
higher, then Maxwell forces B to be higher too such that the energy balance
between electric and magnetic fields is maintained. So even though c =
1/sqrt (e x u), the conclusion I draw is that is is really the electric
permittivity (e) that sets the speed of light:
e (or e0) alone sets the speed of lightCable E and H fields ---another perspective (Nov 15, 06 reply email to Ken Bigelow)
On transmission lines --
The transmission line I have been thinking about is a simple, ideal, cylindrical type (one cylinder inside another cylinder) that is lossless (no R, no G) and can be modeled by a (long) L,C ladder. While it seems counter-intuitive that only reactive components (L & C) can produce a real impedance, this is the case. The reason is that a transmission line is a distributed system, not a lumped system. Look at your equation for Z, which is correct, the j's cancel, Z is real ohms.
An ideal, lossless
transmission line loaded (terminated) with a resistor R where R=sqrt(L/C)
has no reflection from the end. This is the only terminating impedance
that produces no reflection. The proves that the impedance looking into
each LC segment is a real impedance of Z ohms. This fact is in every text
book on transmission lines. And you can find it at this Wikipedia link
too (set ZL=Z0 in their input impedance formula)
http://en.wikipedia.org/wiki/Transmission_line
From the LC ladder here is the argument that E and H in the cable are in phase. Consider the voltage on a capacitor. The E field in the capacitor having units of volts/meter is of course 'in phase' with the capacitor voltage. In the LC ladder there are two inductors connected to each cap, let's call them the input L (toward front) and output L (toward rear). The current in the output L is just the current to the rest of the cable and based on the fact that the impedance of the cable is real (Z ohms) the current in this inductor is also 'in phase' with the capacitor voltage (iout = Vcap/Z).
Now, I was at first troubled by the fact that the current in the input inductor cannot be in phase with the capacitor voltage. The reason is that the current in the input inductor is the (vector) sum of two currents: the output inductor current, which is in-phase with the capacitor voltage, and the capacitor current, which of course leads the capacitor voltage by 90 degrees.
But consider what happens as the LC ladder is made finer and finer with more and smaller LC elements. The finer the LC model the better it represents the distributed L and C of the cable. The current in the output inductor being controlled by a ratio of impedances (v/sqrt(L/C)) is unchanged as L and C get smaller. On the other hand the current in the capacitor approaches zero as the value of each C approaches zero (icap = C dv/dt). So in the limit of a fine LC model, the current in the input inductor approaches the current in the output inductor.
Bottom line --- In the LC model each capacitor represents the local E field (E =v/gap) and the current in the two connecting inductors represent the local H field (H = i/(2 pi r) = (v/Z) x (1/(2 pi r)). Hence the local E and H fields are in phase with the local capacitor voltage and with each other.
This means that if the cable is driven with a voltage ramp (i. e. a voltage that linearly increases with time), as the fields fly down the cable (at 3 x 10^8 m/sec if the gap is air) at each point in the cable the local E (radial) and H (circular) in the gap between the cylinders increase in amplitude together at the same rate. And, it's important to note, the time rate of increase of the E and H field strengths in the cable at any point depends only on the time rate of increase of the external driving voltge. (last sentence is a further thought that was not in the email.)
That's
enough for this email.
Don
footnote (post email)--- Do cable E & H fields have anything to do with photons? In other words is there any way the fields in the cable can be considered photons, or do photons 'arise' only from free unrestrained traveling E and H fields?
Wild, interesting thoughts of physics poster
'photonquark' on photons
A wild physics
poster named photonquark (retired electronic designer!) says this:
We must think of a photon with respect to the size of the observer and the size of the photon. If we see the photon as a small particle, then the fields must be considered in a circular geometry, and if we draw a picture that accurately represents these fields, they will have to have some curvature in them, but if we take any small elemental volume of the fields in the photon, we will have a picture of the orthogonal electric and magnetic field lines that we are used to thinking about. for plane waves.
This is interesting because it applies to the cable fields above. Photoquark concludes that a photon is a sphere of fields with a dia of the wavelength. (He also says E and H are in time quadrature!). More from photonquark
In text books this plane wave is graphed as a sine wave of electric field amplitude, and a cosine wave of magnetic field amplitude, with the sinusoidal waveforms offset by 90 degrees. (really!) Notice that there is no location on this energy wave graph where the photon energy is zero. The sum of the electric and magnetic energy, at any and every instant and location of the wave graph is finite, and never zero. All the energy of the photon is contained within one full cycle of oscillation.
http://forum.physorg.com/index.php?showtopic=1030&st=0
Electromagnetic wave propagation
The
cylindrical cable analyzed is a special case of what is called a waveguide.
The
metal of a waveguide put boundary conditions on the fields (E fields must
enter metal perpendicular). An EM wave that propagatges with no electric
nor magnetic field in the direction of propagation is known as a TEM
(Transverse ElectroMagnetic) wave.
Cylinderical cable reference (confirms H is circular)
http://solar.fc.ul.pt/lafspapers/coaxial.pdf
1/2 C v^2 = 1/2 L i^2 where v and i are at some point in the cable
Note on time relationship of E and H
The 'wrong'
personal site below by Ken Bigelow (came up first in a Google Photon search)
has many pages on light and photons at a low to moderate technical level.
It argues that E and H fields of a light photon, which Ken admits are usually
shown as in-phase, should be in time quadrature (meaning sine and cosine
with a 90 degrees phase difference). The 'right' site is a very nice Power
Point presentation on light from Georgia Tech at an advanced technical
level. Even if you cannot follow the mathematics (div and curl), it's worth
looking at because many characteristics of light are derived and plotted.
A 90 degree time phase difference seems intuitively reasonable because Maxwell's equations show that changing E fields make H fields and vice versa, so how can they both increase and decrease at the same time? Isn't more likely that E creates H, then H creates E, and so on? You often see this simplified explanation put forward for light, it's like a cat chasing its tail. This always made sense to me, and I will admit I was surprised when I found light equations (online) that showed E and H to be in time phase.
Ken's site also makes the argument that E and H in time phase is unreasonable because for an instant twice per cycle both fields will be exactly zero, so Ken asks, "At this time where is the energy?". His solution to this 'problem' is put the E and H fields in time quadrature. Energy stored in a field depends on the field magnitude squared, and there is a trigonometric identity (sine^2 + cosine^2 =1), so with E and H in time quadrature, Ken argues, the energy of a photon is constant. This (naively) seems a strong argument.
However, Ken is wrong. Firstly, it's almost inconceivable that a solution to the light wave equation, first derived 150 years ago by Maxwell, showing that E and H are in time phase could be wrong. What Ken is missing, I think, is an understanding of the frequency of the photon. Its frequency, which can vary over many, many orders of magnitude, depends only on the source of the light and is totally unrelated to the speed of the photon.
The 'zero energy' of photon argument is most easily addressed by considering photons at radio wave frequencies. After all we understand how these photons are generated, they come off of radio antennas. The reason there appears to be zero energy in the fields of a photon at null points in the cycle is because at those times there really is zero energy. And why is that? It is simply because the antenna sends out no energy periodically, twice each cycle of the radio frequency when the AC voltage driving the antenna goes through zero.
It's not unlike 60 hz, single phase, AC power in your home. At null points in the line voltage (every 8.33 msec) you are receiving no power from the power plant. That's why a fast light source like a florescent bulb flickers 120 times per second. Modern electronics that need constant power have large energy storage capacitors in them that provide 'ride-thru' power for a few msec as the line voltage crosses through zero.
wrong http://www.play-hookey.com/optics/transverse_electromagnetic_wave.html
right http://www.physics.gatech.edu/gcuo/
lectures/3803/OpticsI03Maxwell_sEqns.ppt
What's a photon of light?
Photon is
the name given to a specific 'chunk' of light energy that acts (in some
ways) like a particle. For example, a single photon is able to eject an
electron out of atoms such that it can be collected and counted (photoelectric
effect).
Here's one definition --- Where an electron in an atom orbiting the nucleus 'jumps' from a higher orbit at atomic energy level (E2) to a lower orbit at energy level (E1), a photon is emitted (by the electron) that carries away the difference in energy. The relation between the photon energy and its frequency is usually given in the textbooks this way:
freq = (E2-E1)/h
where
h = 6.66 x 10^-34 joule-sec (Planck's constant)
While frequency is easy to define for a repetitive waveform, I find it a somewhat slippery concept when applied to a single photon, especially considering that the quantum physics types are unable to describe its waveform. Hey guys, is a photon like one cycle or not? Apparently quantum physics is silent on this issue, photons are in some sense unknowable.
Visible light is composed of photons in the energy range of around 1.7 to 3 eV. Photon energy is inversely proportioal to wavelength (proportional to frequency). Blue light with a wavelength of 400 nm has energy of 3.1 ev. A red photon with 700 nm wavelength has an energy of (400 nm/700 nm) x 3.1ev = 1.77 ev.
Check
E = h x freq = h x c/wavelength
= 6.66 x 10^-34 x 3 x 10^8/400 x 10^-9
= 0.05 x 10^-17
= 5 x 10^-19 joule
(1 ev = 1 volt x 1.6 x 10^-19 coulomb)
= 5 x 10^-19 joule /1.6 x 10^-19 coulomb
= 3.1 ev
Does special relativity apply to photons?
Well,
time dilation applies to muons traveling near the speed of light.
Muon decay slowed by time dilation is a classic experiment verifying special
relativity.
Time dilation appears to apply to neutrinos. It was not known until recently whether neutrinos had a tiny amount of mass or were massless. Data from new neutrino observatories, built to solve the missing solar neutrinos problem, has shown that neutrinos oscillate their type as they travel from the sun to earth. The argument is given that since we see them changing, they must be traveling slower than the speed of light and have a tiny amount of mass. The clear implication is that if they were massless and traveling at the speed of light, we would see them 'frozen in time' and unchanging .
Time dilation also seems to to apply to troublesome particles, called tachyons, which pop up in the equations of some theories of quantum gravity. These mythical particles go faster than the speed of light. The argument is given that because they are going faster than the speed of light it means that (in some sense) they are traveling backwards in time. This certainly seems to be a time dilation argument to me. Particles approaching the speed of light are seen to go more and more slowly becoming unchanging at the speed of light, and if the speed of light is (theoretically) exceeded, to travel backward in time.
Photon from a relativity point of view
It's very
unlikely this is an original thought, but here goes ---
The muon example, where high speed muons decay much more slowly than what is measured in the lab, shows that as things approach the speed of light we see their 'natural' actions or changes happening more slowly. Well, photons moves exactly at the speed of light. We should see them (in some sense) frozen in time and not changing at all.
Does this not provide an answer as to why the fields of a photon, especially the E field, do not appear to expand with time? Seems to me it might. From a photon point of view after it is 'born' it starts to expand and dissipate, but we see it frozen in time, probably in the state it was in just after it was born.Fast moving objects also appear to us length contracted in the direction of motion. Photons, which travel at the speed of light, must be contracted to the max.
So is it not likely that we see photons contracted in the direction of travel to an impulse function? The effective 'length' of the impulse probably can be figured using the uncertainty principle. The units of planck's constant are energy x time, so from the known energy of a photon (at a known frequency) we can get an uncertainty time, which multiplying by c translates to an uncertainty distance. Contraction to the max in the direction of travel certainly seems consistent with the fact that light is a transverse wave with E and H have no extent in the direction of travel.Not sure if this is directly relevant, but in my reading I have come across another example of things appearing to us as frozen in time. Light from sources in high gravitational fields appears to us red shifted. The argument is made that as the light 'climbs out' of the gravitational field it loses energy, or from another point of view light waveform are stretched out. In a well regarded popular book on black holes by Kip Thorne, (Cal Tech physicist and expert on black holes), Thorne argues that if you were to watch an object falling into a (big) black hole you would see it move more and more slowly at it approached the event horizon of the hole. For example, if it had a regularly flashing beacon you would see it flash more and more slowly.The calculation of a photon's 'length' (in the direction of motion) from its energy and Heisenberg uncertainty principle is very simple. The result (see below, ignoring any 4 pi scaling) is that the 'length' of a photon, meaning the uncertainty in its position in the direction of travel, is just the photon wavelength, which at least for monochomatic light has a well defined meaning.
photon energy E = h x freq
Heisenberg uncertainty E x time = h (min value)
photon 'length' 'length' = c time
= c (h/E)
= c (h/h x freq)
= c/freqIn general (wavelength x freq = velocity), so for a photon (wavelength x freq =c)
'length' = c/(c/wavelength)
= wavelengthDoes length contraction of photons to an impulse in the direction of travel not 'explain' why photons appear particle-like when they interact electrons? In other words does relativistic length contraction not explain the existence of photons?
Now here is the interesting part. As it approaches the 'event horizon' of the black hole, you will see it freeze there (forever). Though 'in reality' the object has fallen through the event horizon and is inside the hole. In fact everything that has ever fallen into the black hole you will see (in some sense) piled up on its event horizon 'surface'.
Waves & photons
A response
on a physics blog made an interesting point. Light appears particle-like,
i.e. as a photon when it is observed meaning when it is emitted or absorbed.
Light acts wave-like when it is not observed, for example, going through
double slits.
"The premise is that while it is a wave it is "wholly" a wave and when it is a particle it is not a wave. We only "see" light when it "interacts" as a particle. It is important to understand that when it is a wave it is not a particle. This is the unobserved state of a quantum." ."An impulse in the time domain is an ensemble of frequencies in the frequency domain. It is a truncated wave train."How does the eye see color?
The eye might (theoretically) be able to sense directly the frequency and/or energy of light photons it receives. But to sense lots of slightly different colors this way very likely means the eye would need many, many different photosensitive molecules with a range of energy levels making this very unlikely.
But there is a simpler was to sense color. This is the method used in color film and in digital cameras, and it is used by the eye too. The light is measured three times by broadband detectors each optimized for one of three primary colors (R, R, B). In a digital camera surface of the CCD detector has an array of primary color (R, G and B) filters above identical light (intensity) detectors. By knowing how strongly the R, G, and B optimized detectors respond the color of the light is determined.
In the eye this is done by three types of cone cells. Each type of cone cell is sensitive to a fairly wide range of photon frequencies (energy) with one type most sensitive to short wavelengths (blue), one medium wavelengths (green), and one long wavelengths (red). See below. Note that shape and gain of these curves must be quite stable for the brain to correctly interpret the ratio of the three cone cell outputs it gets as color. It (apparently) takes a thousand or more photons to get an output form a cone cell.
three types of cone cells
The eye also contains (lots of) much more sensitive cells called rod cells. These are the cells that can be triggered by 1 to 5 photons. These cells are used when light is dim. Since there is only one type of rod cell and its response is quite wideband (see below), there is no way to figure the color of these photons. In effect rod cells act as photon counters with the light intensity being proportional to the photon count. {To get a (normal) image the photon count needs to be scaled by a non-linear curve called the gamma curve, but we won't go into that here. You can read about this in references of digital camera CCD's.}
rod cells
color and wavelength
Rods and cones both sense light with retinal, a pigment molecule, embedded in (different) proteins. A photon hitting reinal causes an electron to jump between energy levels created by a series of alternating single and double bonds in the molecule causing a twisting of the molecule. The change in geometry initiates a series of events that eventually cause electrical impulses to be sent to the brain along the optic nerve.
Rods are incredibly efficient photoreceptors. Rods amplify the retinal changes in two steps (with a gain of 100 each for a total gain of 10,000) allowing rods (under optimal conditions) be triggered by individual photons. Cones are one thousand times less sensitive than rods, so presumably takes a minimum of 1,000 photons to trigger a cone.
Here is measured voltages in rods excited by repeated very dim light flashes ('dots'). The interpretation of the data is that the rod output voltage is both quantized (indicating photons) and proportional to the number of photons sensed (0,1,or 2).
no pulse ( 0 photon), small pulse (1 photon),
large pulse (2 photons)
Retinal in solution when exposed to light changes to different isomers depending on the wavelength. It is found that the spectral response of retinal in solution is the same as the spectral response of the eye, so it must be (mostly) retinal that sets the wide spectral response of cells of the eye..
Cone vision is much sharper than rod vision. It's a resolution issue related to how the cells are 'wired' to the brain. Each cone cell connects to a different optiic nerve fiber, so the brain is able to precisely determine the location of the visual stimulus. Rod cells, however, may share a nerve fiber with as many as 10,000 other rod cells.
In resolution terms 7 million cones cells translates to 7 mpixels (or maybe 2.33 mpixel triads) equivalent to a digital camera. If the 120 million cones are wired in, say, 1k bundles, then rod resolution would be 1.2 x 10^8/10^3 = 120,000 pixels, which is pretty low.
Good eye links:
http://photo.net/photo/edscott/vis00010.htm
http://www.chemistry.wustl.edu/~edudev/LabTutorials/Vision/Vision.html
How photons are sensed by retinal in the eye
Retinal
is a relatively simple molecule with about 35 atoms (total) of hydrogen
and carbon that is the light 'detector' in rod cells and all three types
of cone cells. One particular double bond of retinal can ' break' (in 0.2
picosec) if an electron in the bond absorbs a visible photon of light and
is excited. With the bond broken the end of the molecule rotates (in nsec).
This shape change affects the protein to which retinal is attached and
begins a cascade leading to the firing of a nerve impulse to the visual
cortex of the brain. While retinal is the light sensitive molecule in both
rods and cones, the proteins are different, the cascades are different
and the gains are different in the different cell types.
Two eye photon puzzles
I was unable
to discover an explanation of two key issues related to photon sensing
by the eye.
a) What is the mechanism that widens the photon frequency absorption spectrum? How is the curve so stable and predictable?
b) How is it that 1,000+ photons are needed to fire a cone cell. Does it require that 1,000+ molecules of retinal in a cell be activated? Over what time interval must the 1,000+ photons arrive?
Broad frequency response puzzle
Not only is
the photon absorption frequency range of eye cells very wide, it must be
stable and predictable too (at least in cone cells) othewise the brain
would not be able to ratio the outputs of the different cone cell types
to determine color.
The basic puzzle (to me) is that the frequency spectra of atoms and molecules, both emission and absorption, due to an electron changing orbit is always shown as a collection of seemly randomly spaced very narrow lines, not at all like the wide, smooth absorption spectra of eye cells Why is the eye absorption so different? Is it a thermal effect? Are there other examples of wide spectra?
Thermal energy makes wide, continuous spectra. When electrons vibrate thermally, they emit a wide spectrum of frequencies that depend on the temperature. There is an ideal model of this type of wideband, thermal radiation called black body radiation. It has specific calculable, energy vs frequency curve that varies with temperature and is the same for all materials.
Spectrum of an incandescent bulb in a typical flashlight
(4,600K)
The sun is (very close to) a black body with a surface temperature of 5,780 degrees kelvin. A prism, by it ability to spread sunlight into a rainbow spectrum, neatly demonstrates that the atoms near the surface of the sun (likely hydrogen and helium) are emitting a wide spectrum of frequencies. A hydrogen atom has both continuous and discrete spectrum; the continuous part represents the ionized atom.
Are the atoms on or near the surface of the sun that emit visible sunlight ionized? A NASA reference on the sun says this: "much of the sun's surface (about 6,000 degrees) consists of a gas of single atoms", however, both the inside of the sun and its corona are (largely) ionized. Since the sun is more than 90% hydrogen, most of the inside the sun is a plasma of independent protons and electrons. The corona of the sun reaches millions of degrees.
Ideas/thoughts
a) It's a thermal/heat effect --- The narrow spectra shown are often astonomical
and when measured in the lab the gas density is very low.
b) It's somehow related to the nature of the double bond and/or stress
in the bond, perhaps modulated somehow by the protein to which it is attached?
c) Intermediate molecules exist with sensitivity peaks at different frequencies.
Con -- these intermicate peaks are shown as wide too.
d) Maybe there are a lot of slightly different variants of the light sensitive
molecule in each cell, so it's a statistical thing? The broad curves
is really a mixture of narrow curves. Con -- not even a hint of this in
references.
a) seems most likely --- Here is Wikipedia on emission spectrum ---- When the electrons in the element are excited, they jump to higher energy levels. As the electrons fall back down, and leave the excited state, energy is re-emitted, the wavelength of which refers to the discrete lines of the emission spectrum. Note however that the emission extends over a range of frequencies, an effect called spectral line broadening.
Can our cable model help us understand light photons?
Let's put
an electric signal with the frequency of (blue) light into our idealized
(lossless) cable. For the LC model of the cable to work we need a minimum
of two LC segments per cycle of the maximum frequency in the cable, one
seqment for each polarity reversal. Quantum mechanics tells us the frequency
of light is proportional to its frequency, but my understanding is that
the more general rule is that the energy of a photon depends on the rate
of change of E and H fields.
. Assuming a (fairly high) excitation voltage it's easy to calculate the peak energy in the each segment L and C, which are the same as the field energies in a half wavelength segment of cable. In this way (for the excitation amplitude we assumed) we should be able to come up with the photon density, and since the energy of a blue photon is known from quantum mechanics, we can find out the extend of the field of one photon and how it varies with field strength.
Here are the cable formulas. We substitute e0 for e and u0 for u, since we want our cable model to heop us understand light propagation. We'll use a very fine resolution of our LC ladder model setting the length to be the wavelength of blue light.
L (per length h) = u0 x h x d/(2 pi r)
C (per length h) = e0 x h x (2 pi r)/d
Z (cable impedance) = d/(2 pi r) x sq rt (u0/e0)
where
h = 2 x 10^-7 m
(section of a long cable = 1/2 wavelength of blue light )
r = 5 x 10^-3 m
(5 mm radius to center of gap)
d = 10^-3 m
(1 mm gap between cylinders)
v = 100 volt
(0 to 100 V applied voltage step)
reference
u0 = 4 pi x 10^-7 h/m
e0 = 8.8 x 10^-12 f/m
Z free space
= sq rt (u0/e0) = sq rt (4 pi x 10^-7/8.8 x 10^-12)
= 377 ohms
frequency (blue)
= 7.5 x 10^14 hz
1/2 wavelength (blue)
= 2 x 10-7^m
0.5 x (c/freq)
1/2 period (blue)
= 6.66 x 10^-16 sec
energy of photon
(blue) = 5 x 10^-19 joule
(Planck's Constant x freq)
L (per length h) = u0 x h x d/(2 pi r) = 4 pi x 10^-7 x 2 x
10^-7 x {10^-3/(2 pi 5 x 10^-3)}
= 25 x 10^-14 x .032
= 8 x 10^-15 henry
C (per length h) = e0 x h x (2 pi r)/d = 8.8 x 10^-12 x 2 x
10^-7 x 31.4
= 552 x 10^-19
= 5.5 x 10^-17 farad
Z (cable impedance) = d/(2 pi r) x sq rt (u0/e0)
= .032 x 377 ohm =12 ohm
check
Z =
sq rt (L/C) = sq rt (8 x 10^-15/5.5 x 10^-17) = 12 ohm (OK)
input current = i = v/Z = 100 V/12 ohm
= 8.33 A
input power = v x i = 100 V x 8.33 A
= 833 watts
velocity of signal = delta position/delta time = h/sq rt (L x C)
= 2 x 10^-7/sq rt (8 x 10^-15 x 5.5 x 10^-17)
= 2 x 10^-7 m/6.63 x 10^-16 sec
= 3.0 x 10^8 m/sec (speed of light in vacuum)
energy in L = 0.5 x L x i^2 = 0.5 x 8 x 10^-15 x (8.33)^2
= 2.78 x 10^-13 joule
energy in C = 0.5 x C x v^2 = 0.5 x 5.5 x 10^-17 x (100)^2
= 2.75 x 10^-13 joule
total field energy = 2 x 2.75 x 10^-13
= 5.5 x 10^-13 joule
check
energy in electric field = 0.5 x e0 x E^2 x volume
= 0.5 x 8.8 x 10^-12 x {100 V/10^-3 m}^2 x {2 pi x r x d x h}
= 0.5 x 8.8 x 10^-12 x {100 kv}^2 x {31.4 x 10^-6 x 2 x 10^-7} m^3
= 0.5 x 8.8 x 10^-12 x 10^10 x 6.28 x 10^-12
= 2.75 x 10^-13 joule OK
check
power into cable = total energy in fields of segment/ time constant of
segment
= 5.5 x 10^-13 joule/6.66 x 10^-16 sec
= 827 watts OK
To find the number of (blue) photons in the seqment of cable length one bule wavelength long we just divide the total field energy by the known energy of a blue photon
# of photons in seqment = energy in E and H fields/energy in blue photon
= 5.5 x 10^-13 joule/ 5 x 10^-19 joule
= 1.1 x 10^6
To find the
density of photons we divide the number of photons in the cable segment
by the area of the circular ring made by the gap (looking into the cable)
photon density = # of photons in seqment/{2 pi x r x d}
= 1.1 x 10^6/ 31.4 x 10^-6 m^2
= 3.5 x 10^10 photons/ square meter
The area occupied by each photon is the inverse of the photon density and the linear spacing between photons is (about) the sq rt of the area occupied by each photon.
photon to photon spacing = sq rt (1/photon density)
= sq rt (1/ [3.3 x 10^10] photons/ square meter)
= sq rt (0.286 10^-10)
= 5.3 x 10^-6 m
check
# of photon
in segment = area of gap ring/area occupied by each photon
= (2 pi x r x d)/(photon-photon spacing)^2
= (31.4 x 10-6 m^2)/(5.3 x 10^-6 m)^2
= 31.4 x 10-6 m^2 /28 x 10^-12 m^2
= 1.1 x 10^6 photons OK
Conclusion
With
these two assumptions:
photon length = 1/2 wavelength
E field strength = 10^5 v/m
or (100v/1 mm)
we calculate that the energy in the electric and magnetic
fields of half (blue) wavelngth of cable is (about) 1 million times the
energy of a blue photon. Since the energy density in the cable's small
gap is uniform, I think we are justified at saying that (about) 1 million
(blue) photon reside in the a lenght of cable 1/2 wavelenght. And
at an E field strength of 100kv/m each photon occupies (about) 1 millionth
of the field volume.
Alternatively we can reduce the driving voltage by 1,000
(100V => 100mv). This will reduce the energy in both the E and H fields
by one million, so that the energy in the gap of this 1/2 (blue) wavelength
of cable is equal to one (blue) photon. In this case we get:
volume = cable section length x 2 pi radius x gap
= 2 x 10^-7 m x x 2 pi 5 x 10^-3 m x 10^-3 m
= .0002 mm x 6.28 x 5 mm x 1 mm
= .0062 mm^3
E field strength = 100 mv/1 mm = 100 V/m
Conclusion
At 100V/meter (E fiield strength) the energy of one blue photon (5 x 10^-19
joule) fits in a volume a little less than 1% (0.62%) of a cubic mm. The
geometry is a very thin (.0002 mm) ring with a dia of 1 cm and a width
of 1 mm. The ring dimensions dictated by the cable and the thickness by
1/2 wavelength of blue light.
If the ring
dimensions (cable size) is scaled we can keep the energy constant at 1
blue photon equivalent by scaling the fields by the ring scaling, as shown
in the table below. The ring thickness is 1/2 wavelength of a blue light
and the width of the ring is 1/10 th of the ring dia..
| ring thickness | ring dia | E amplitude |
| 2 x 10-7 m | 1 m | 1 V/m |
| 2 x 10-7 m | 1 cm | 100 V/m |
| 2 x 10-7 m | 10^-6 m | 10^6 V/m |
| 2 x 10-7 m | 10^-10 m | 10^10 V/m |
We can say a 'cable type blue photon' (or photon equivalent) can be a tiny ring the size of an atom with an E field strength of about one million volts/meter, or it can be a large 1 cm dia ring with an E field strength of 100V/m, or anywhere in between..
The last entry in the table is suggestive because it seems a good match with atoms that are known to emit and absorb photons. It shows a photon as a tube, 500 times longer than it is wide, with a dia othat matches that of an atom.
Some questions about the light model
Is all the energy in the E and H fields?
Pretty sure answer is yes
(Is this type of classical model valid, or must it be quantum mechanical?)
What is the ratio of E field to H field energy?
H
= sq rt (e0/u0) x E or B=u0H = E/c
(see also calculation above)
result is that energy in E and H fields are exactly the same
Are photons particles?
Feymann in his video lecture on photons (see link) hammers home the point
that photons are particles. He says the clicks from a photomultiplier tube
(photon detector) sound just like rain drops hitting (when light
intensity is very low). Brighter light (of same color) is just more photons/sec.
How wide is the cable/pipe?
can
it be estimated from light energy?
above Gorgia Tech Power Point link give the photon flux of bright sunlight
as
10^18 photons/sec-m^2
since blue light freq = 7.5 x 10^14 hz if (as a though experiment) the
photons are viewed
as lined up in a row in repetive E and H cycles ('photon streams'), then
the number of
these streams per m^2 is {10^18 photons/sec-m^2/7.5 x 10^14 hz (blue light)}
=
1,300 photon/m^2, which means the photon streams are incredible far apart.
The
distance is sq rt (1,300) which is about 2.7 cm or more than 1 inch apart!
As a reasonableness check on the photon flux let's calculate
the joules/sec (watts) of bright sunlight on a meter square (will use the
energy for blue light)
Energy/m^2-sec = 10^18 photons/sec-m^2 x 5 x 10^-19 joule/photon
= 0.5 joule/sec (or 0.5 watt) for m^2
Check --- Whoops, I find (online) summer sunlight is
130 mW/cm^2, which is pretty reasonable (maybe a little high). Then the
power of a one meter^2 scollector would be 130 x 10^-3 x 10^4 = 1,300 watt/m^2.
(Another reference gives 1,000 watt/m^2). This 2,600 times higher than
the photon reference, but still even at this level the photons spacing
is reduced by only sq rt (2,600) which is about 50, or from about 27 mm
to
about 1/2 mm.
Bottom line --- photons in bright sunlight are hugely spread out.
Another flux
given is of a tightly focues laser beam. This number is 10^26 photons/sec-m^2
or 10^8 higher than bright sunlight. Focused laser light reduces the spacing
between 'photon streams' by sq rt (10^8) = 10^4. So the side to side spacing
goes from 2.7 x 10-2 m down to 2.7 x 10-6 m ( 2.7 cm down to 2.7 microns).
--------------------------------------------------------
Whatis a photon? Is a photon one cycle? half
cycle? a specific energy value?
good
question. I never see this addressed. A poster to a physics forum agrees
saying, 'most physicists, professors, and textbooks don't do a good job
of describing the photon'.
Einstein pointed out that many anomalous experiments could be explained if the energy of a Maxwellian light wave were localized into point-like quanta that move independently of one another, even if the wave itself is spread continuously over space.
Below is very useful stuff from this physics forum
http://www.physicsforums.com/showthread.php?t=104657&page=2
** A photon corresponds to the energy dE associated to the transition of an EM-field from one configuration to another.
** Photons are not EM waves. EM waves are an emergent property of large numbers of photons.
QED, interaction of photons and electrons, has been verifed to by experiment to 10+ decimal places. Photons are fundamental. As far as we know photons are on the same level as the other fundamental particles of the Standard Model, the quarks, leptons, and (remaining) gauge bosons.
In Maxwell's theory the energy depends on the magnitude of E and H.
It is said the human eye can see color starting with as little as 5 photons striking the eye, likely a very short interval. These photons can arrive with completely random spacings though such as light from the sun, lightbulb, or an image. With the photons randomly spaced about the only think the eye can do is detect the individual photon energy and average it to trigger a nerve signal.
For reference a typical 'photon' detector is a photomultiplier tube. It works on the photoelectric effect. Photons stiking a metal plate knock electrons free from their atoms, and the freed electrons are collected by a voltage to form an output current from the tube. If light of a specific color causes elctrons to fly out with a certain speed, then increasing the light intensity results in more electrons with the identical speed.
A single free
electron can be detected by the resulting cascading electron pulse it creates.
One electron knocked free is interpreted (using Einstein's photoelectric
theory) as the detection of a single photon.
Here is an 1 hr 17 min video recording of Feymann lecturing
on the photon
http://www.vega.org.uk/video/subseries/8
How big is a photon?
To get a rough
idea of the 'size' of a photon we can use Heisenberg's uncertainty principle,
which is one of the basic building blocks of quantum mechanics. The uncertainty
principle says the (minimum) uncertainty in position is the momentum (which
we know) divided by 5 x 10^-35 joule-second, which is just planck's constant
divided by 4 pi (h/4 pi). However, we don't need to work any numbers because
the momentum of a photon also depends on planck's constant (p = h/wavelength).
The result is the uncertainty in position of a photon is the photon wavelength
divided by 4 pi.
photon position
from Heisenbery uncertainty principle
position = heisenberg/momentum
= (h/4 pi)/(h/wavelength)
= wavelength/4 pi
Wikipedia explains
this was arived at by Heisenberg as the the wavelength divided by 2 pi,
which is a radian, and the standard deviation of a bell shaped uncertainty
was 1/2, combined to give 1/4 pi.
-------------------------------------------------------------
How specifically does the energy in the fields go
up with frequency?
-- larger amplitude or bigger radius? (length goes down right?)
Where is the energy the instant both fields have zero
ampliture
there is no (light) energy at these times
Consider radio photons that come from radio antennas. When the driving voltage on the antenna is at zero voltage (twice each cycle) no power (P = v x i) is delivered to the antenna, so no power is sent by antenna. That's why periodically in the light beam there are times of no energy. The frequency (wavelength) of photons is determined (totally) by the source and is unrelated to the speed of the photons.
Riff on the 'missing' term Maxwell found
Maxwell was able to condense all the many known electric and magnetic rules and formulas, which had been teased from mother nature by a huge number of experiments by Faraday and others, into four short equations. But Maxwell made his own original discovery; he found a relationship that had been missed by all the earlier investigators. He discovered (mathematically) another type of current, called a displacement current.
There is a puzzle with current flow inside capacitors (Lyden jars), which apparently had never been appreciated prior to Maxwell's time. In simple terms a capacitor is two plates separated by an insulator. When the voltage across a capacitor is changing, current flows in one lead of the capacitor and comes out the other (I = C dV/dt). The puzzle is this: 'How the hell does the current get through the insulator (which can even be a vacuum!) between the plates?'
A changing voltage means the E (or D) field in the capacitor, which all drops across the insulator, is also changing, because the units of E are volt/meter. Maxwell came to understand that the changing E (or D) field in the insulator was like a current (he called it a displacement current), and this was how the current got through the capacitor. Ampere's law allows H (around a loop) to be calculated from current passing through the loop. In his equation Maxwell expanded the Ampere Law equation to include a 2nd current term that was equal to the d/dt of the E field passing through loop.Line Integral {H ds} = i before Maxwell
where
k = 1/u0 x c^2
Discovery that light is an electromagnetic wave
It may at
first have seemed to Maxwell that adding this extra term was just a clean
up of the equations, but it was soon to lead to one of the major breakthrough
in 19th century physics. The equations now had a kind of symmetry in that
a changing magnetic field (H) creates an electric field (E), and a changing
electric field (E) creates a magnetic field (H). When Maxwell studied his
equations, he found that a self-sustaining, freely propagating, electromagnetic
wave was possible.
Maxwell found the wave would travel at a fixed speed equal to 1/sqrt (eo uo). The constants e0 and u0 were known from electric and magnetic tests, and when Maxwell plugged in the numbers, he was astounded to find the wave's speed was 3 x 10^8 m/sec. He was astounded because he knew that this was very close to the speed that astronomers' had calculated for light. Maxwell concluded, based on the close speed agreement, that light, whose nature had been argued over for hundreds of years, was (very, very) likely an electromagnetic wave. His friend, Faraday, had long suspected this, but couldn't prove it!
Precedents --- Above is how the story is usually told, but the history of the speed of light from electric/magnetic parameters is a little more complex. With hind sight it can be seen that there were precedents.The fact that Maxwell's equations predicted that an electromagnetic wave travels at a fixed speed (not dependent on the speed of the source) would also later turn out to be very important. It was a clue that something was wrong with the Newtonian notion of fixed time and space, and it led directly to Einstein's 1905 paper on special relativity, titled "On the Electrodynamics of Moving Bodies".About 10 years before Maxwell, Kirkoff realized that a velocity could be extracted by combining electric and magnetic parameters and suspected that electrical signals traveling down wires were going at this rate. Weber and Kohlrausch (in 1856) had an electromagnetic theory that included a similar maximum speed, but for some reason they included a sqrt(2) multiplier. They did measurements and came up with the value 4.39 x 10^8m/sec. Their value, when corrected to remove the sqrt(2), was 3.1 x 10^8 m/sec, pretty close to the right value
The bottom line is that others before Maxwell had found that electrical signals moved down wires very fast (perhaps at the speed of light) and that it was possible to extract a speed in the neighborhood of the speed of light from electrical parameters. Maxwell's claim on history remains strong, however, because he tied the right value to an electromagnetic wave equation that suggested an explanation for light.
First measurement of speed of ight using Jupiter's
moons
The four brightest
satellites of Jupiter were first seen by Galileo with his small telescope,
and he diagrammed their orbits in his book on the telescope. The closest
of them orbits Jupiter in less than two days. They are all fairly close
to Jupiter and tiny compared to Jupiter, so they are eclipsed regularly
by Jupiter. Astronomers love eclipses because they can often be timed to
the second. Jupiter's eclipsing bright satellites were often considered
a 'clock in the sky'. Accurate time measurements (with a lot of work) translate
into improved knowledge of orbits and distances.
In 1676 Roemer, a Danish astronomer working at the Paris Observatory, was doing a systematic study of Io, one of the moons of Jupiter. Roemer found over several months eclipse times got more and more behind predicted times, reaching a maximum error of about 22 minutes, and then over several months the lateness of the eclipses got smaller and smaller. This cycle repeated. He noticed that the period (time of one cycle) of his eclipse variations could be explained by looking at the orbits of the earth and Jupiter (see Roemer's sketch). He proposed that the explanation of the eclipse timing errors was that as Earth moved in its orbit further away from Jupiter the light had a longer distance to travel, so it took additional time to reach the Earth. From his measured maximum eclipse timing error (22 minutes) combined with the then best estimates of the diameter of the earth's and Jupiter's orbits he was able to come up with the first reasonable accurate measurement of the speed of light. Roemer figured the speed by dividing his measured maximum late time by (approx) the diameter of the earth's orbit.
Light Speed (est) = 2 x 93 million miles x (1.61 km/mile)/22 minutes
= 300 million km/1,320 sec
= 0.227 million km/sec
= 2.27 x 10^8 m/sec
.
Here is a reproduction of the original drawings by Roemer
delineating his methodology utilized to determine the speed of light.
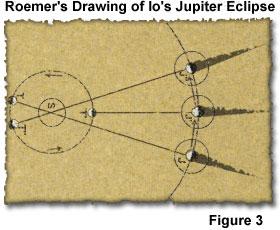
Roemer eclipse timing errors were off on the high side (modern value is 17 minutes), so his measured value for the speed of light was a little low (25% low). Eleven year later (1687) Newton wrote in Philosophiae Naturalis Prinicipia Mathematica (Mathematical Principles of Natural Philosophy), "For it is now certain from the phenomena of Jupiter's satellites, confirmed by the observations of different astronomers, that light is propagated in succession and requires about seven or eight minutes to travel from the sun to the earth". Newton had a pretty accurate value.
Another early speed of light measurement
About 50 years
after Roemer (in 1728) astronomer James Bradley figured out another way
to measure the speed of light. He realized that the angle you need to point
the telescope to see a star (after correcting for earth rotation about
its axis) should change a little over six months as the earth orbits the
sun. It has nothing to do with parallax (nothing to do with how far away
the star is). It is an effect that depends only on the speed of
earth (in orbit around the sun) compared to the speed of light. Technically
this phenomena is called 'stellar aberration'.
One way to understand this is to visualize the photons coming down a long telescope tube that is moving. The tube needs to tilt a little (in the direction of travel) so that the photons come straight down the tube. There is also the classic rain analogy:
Imagine starlight as a steady downpour of rain on a windless day, and think of yourself as walking around a circular path at a steady pace. You (everywhere on the path) see the rain not coming vertically downwards, but at a slant toward you. Say the rain is falling at 30 mph and you are walking at 3 mph, you see the rain with vertical speed of 30 mph and a horizontal speed (towards you) of 3 mph. Drawing a triangle you find the rain coming in an angle (from vertical) of tan^-1{3 mph/30 mph} = 11.3 degrees, and so you tilt your umbrella 11.3 degrees forward to best protect yourself. At one point on the path the umbrella tilt angle will be, say, east and half way around the path it will be west. Seen by an outside observer your umbrella angle around the path varies by 2 x tan^-1{ratio of speeds}.The earth goes around the sun at about 18 miles/sec, and Bradley knew from Roemer's measurement that light's speed was about 180,000 miles/sec or about 10,000 times faster. So for a star visible for six months (say in the northern sky?) the angle of the telescope from vertical will differ over six months by about 2 x tan^-1 (1/10,000) or 2 x 10^-4 radians = 0.011 degrees or 41 arc-sec. The six month change in angle you measure is proportional to the ratio of the earth's speed to the speed of light. Bradley was able to measure this angle quite accurately, and (apparently) the size of the earth's orbit was also known at the time quite accurately, such that his value for the speed of light (185,000 miles/sec or 2.98 x 10^8 m/sec) was accurate to within 1%.
19th century measurements of the speed of light
The
technical problem of measuring the speed of light directly on Earth was
solved in France about 1850 by two rivals, Fizeau and Foucault, using slightly
different techniques. In Fizeau's apparatus, a beam of light shone between
the teeth of a rapidly rotating toothed wheel, so the "lantern" was constantly
being covered and uncovered. Instead of a second lantern far away, Fizeau
simply had a mirror, reflecting the beam back, where it passed a second
time between the teeth of the wheel. The idea was, the blip of light that
went out through one gap between teeth would only make it back through
the same gap if the teeth had not had time to move over significantly during
the round trip time to the far away mirror. It was not difficult to make
a wheel with a hundred teeth, and to rotate it hundreds of times a second,
so the time for a tooth to move over could be arranged to be a fraction
of one ten thousandth of a second. The method worked.
Foucault's method was based on the same general idea, but instead of a toothed wheel, he shone the beam on to a rotating mirror. At one point in the mirror's rotation, the reflected beam fell on a distant mirror, which reflected it right back to the rotating mirror, which meanwhile had turned through a small angle. After this second reflection from the rotating mirror, the position of the beam was carefully measured. This made it possible to figure out how far the mirror had turned during the time it took the light to make the round trip to the distant mirror, and since the rate of rotation of the mirror was known, the speed of light could be figured out. These techniques gave the speed of light with an accuracy of about 1,000 miles per second.
In 1879 Michelson in the US improved on Foucault's method. Instead of Foucault's 60 feet to the far mirror, Michelson had about 2,000 feet along the bank of the Severn, a distance he measured to one tenth of an inch. He invested in very high quality lenses and mirrors to focus and reflect the beam. His final result was 186,355 miles/sec (x 1,609.3 m/mile = 2.999 x 10^8 m/sec), with possible error of 30 miles per second or so. This was twenty times more accurate than Foucault.
Speed of light is in the moslem Quran?
For
fun check out this site. They claim you can pull out the speed of light
in a vacuum from the Quran to 7 decimal places! It gives a
lot of detail as to how they calculate it. I have only quickly glanced
at their equation, but I don't see an obvious fudge factor in it. Seems
hard to believe there is not a fudge somewhere. I have checked the math
with my pocket calculator, and while the resolution is slightly beyond
my calculator's range, the math does look like it's probably OK.
After doing a little tiptoeing through the tulips (for example, angels mean light, 1,000 lunar years means 12,000 orbits), they claim the Quran gives this simple formula for the speed of light: distance the moon travels in 12,000 orbits divided by one day. Their final equation is this
c = 12,000
x 3,682.092 km/hr x 655.71986 hr x 0.8915645 / 86,164.0906 sec
= 1.2 x 10^4 x 3.682092 x 10^6 m/hr x 6.5571986 x 10^ 2 hr
x 0.8915645 / 8.61640906 x 10^4 sec
= 2.997925 x 10^8 m/sec (they get)
= 2.9979244 x 10^8 m/sec (their equation, my calculator)
(2.99792458 x 10^8 m/sec -- in 1983 meter definition was changed
making this the exact value for c)
where
12,000
is orbits from Quaran
3682.092 km/hr is equal to 2pi x average circular radius (38,4267 km) divided
by
sidereal luman month (655.71986 hr). They say NASA's value for
the average lunear speed (range from 3470 to 3873 km/hr) is 3682
km/hr
655.71986 hr is the sidereal luman month
0.8915645 is cos (26.92952225 degrees)
where 26.92952225 degrees is derived from the ratio of one heliocentric
revolution to one year
ø = 27.32166088 days x 360 degrees / 365.2421987 days
86164.0906 is sec in a sidereal day (with respect to stars) of 23 hr, 56
min, 4.0906 sec
As a cross check of ø, I found at another site
Tropical Month = 27.3216 days. It is the time taken for the Moon to complete
one 360 degree cycle of the ecliptic circle from spring equinox to spring
equinox.
Tropical Year (or Solar Year) = 365.2422 days. It is the time taken
for the Sun to complete one cycle of the ecliptic circle from spring equinox
to spring equinox.
Capacitors & Inductors
Parallel plate
capacitor and a good explanation of how material increases the dielectric
constant.
http://www.pa.msu.edu/courses/2000spring/PHY232/lectures/capacitors/twoplates.html
What about astronomical red shift?
For a long time it was unclear to me how astronomical red shift was consistent
with the relativity. Consider, a fundamental principle in relativity is
that the speed of light you measure from a moving source is unaffected
by
the speed of the source. Yet in astronomy the light from galaxies and stars
is affected by their speed (relative to us). The frequency shift
of absorption lines in the spectrum of astronomical objects (relative to
the frequencies measured in the lab) is used as a measure of their speed
relative to earth. Sometimes you see the red shift 'explained' as being
a Doppler shift. In the case of galaxies the reddning of light is sometimes
'explained' as due to the expansion of space while the light has been traveling
to us.
The explanation is that astronomical red (& blue) shifts are changes in the frequency (color), energy and momentum of the light caused by the velocity of astronomical objects relative to us. Technically known as the relativistic Doppler effect. The energy light carries is proportional to its frequency. When a source is moving toward us, it moves a little forward during the time of each cycle of light, so the time we see between the peaks of sucesive cycles is reduced of the cycles is reduced, we see the frequency higer. Similarly we see the frequency lower when the source is receeding from us. Note light's frequency and speed of propagation are totally different and not related. The speed of the light from an astronomical body does not depend on its speed (relative to us) and is the same for all frequencies.
New confirmation that speed of light is the same for
all frequencies
A good, recent,
proof that speed of light is the same for all frequencies is a mysterious
astronomical object known as a gamma ray burster. This 'light'
has a huge has red shift which means it has traveled for billions of light
years to get to us, yet we see it as a short pulse of a second or so. Any
pulse by Fourier analysis is mixture of many different frequencies. If
light of different frequencies traveled at (even slightly) different speeds,
as for example ocean waves do, then we would not see gamma ray bursters
as short pulses. Gamma ray bursters because of their pulse character and
great distance provide a stringent test of the thesis that light of different
frequencies travel through space at the same speed.
spaceship firing short light bursts
neutron stars ---doppler away
& closer and?? time dilation v^2
also gravitational red shift --
frequency shift of light from white dwarfs (neutron stars?
--- general relatitivity effect
References
Charge of
an electron = 1.6 x 10^-19 coulomb
Mass of an
electron = 9.1 x 10^-31 kg
magnetic permability
u0 = 4 pi x 10^-7 (1.26 x 10^-6) h/m
electric permativit
e0 = 8.8 x 10^-12 f/m
h = Planck's
Constant = 6.626 × 10^-34 joule·seconds (4.135
× 10^-15 eV·sec)
Ångstrom
= 10^-10 meter
Heisenberg
uncertainty = delta position x delta momentum
= delta position x delta velocity
= delta energy x delta time
= h/4 pi
= 5 x 10^-35 joule-second
Blue light
blue light
frequency = 7.5 x 10^14 hz
blue light
wavelength = c/freq
= 400 nm = (3 x 10^8 m/sec/7.5 x 10^14 hz)
= 4 x 10-7^m
(E) energy
of photon (blue) = h x freq
= 6.6 x 10^-34 x 7.5 x 10^14
= 5 x 10^-19 joule (3.1 ev)
(p) momentum
(blue) = mv = (E/c^2) x v = (E/c^2) x c
= E/c
= (5 x 10^-19 joule/3 x 10^8)
= 1.67 x 10^-27 joule-sec/m
= (h x freq)/wavelength x freq)
= h/wavelength
= 6.6 x 10^-34/4 x 10^-7
= 1.65 x 10^-27 joule-sec/m
---------------------------------------------------
In a classical wave picture, the slowing can be
explained by the light inducing electric polarization in the matter, the
polarized matter radiating new light, and the new light interfering with
the original light wave to form
@@@@@@@@@@@@@@@@@@@@@@@@@@@@
physics postings
If photons are indeed quasi-monochromatic wave packets, and not plane waves of infinite transverse extent, there must be a charge sheath just like a waveguide. I solved for this charge and current with Maxwell's source equations. I assume Gaussian exponential decay in three dimensions, of a one-frequency wave. I gather QM does not allow discussion of such, fundamentally. I have, and the results speak, once again, to necessary phenomenology of the vacuum polarization field. There is a simple characterization of magnetic vector potential "A" acting to 'plow' the vacuum, throwing opposite charges, or creating a trasverse current. These ebb and flow according to continuity in the sheath. In a helical photon, there are two nested double helices of opposite polarity..................If indeed the vacuum responds this way, I reason that these infinitesimal manifestations leave no way for the packet's total energy to be necessarily quantized. I say quantization is the property of the emitter and not fundamentally of the vacuum. Yes of course there is a large population of quantized photons but this is no reason to assume that to be the only possible mode of the field. I argue the quantum hypothesis was overextended here. http://laps.noaa.gov/albers/physics/na
Above author (Norman Albers)writes (wild) math papers about photons. He argues there is some unexplained character of the vacuum that somehow produces virutual charge or dipole pairs that act to terminate spacially the E and H filelds of a photon.
** experimentists are working on 'photon pistol', a device to generate single photons. These people publish peer reviewed papers. Search word 'Fock', 'quantum optics' "it is much easier to define a single-photon pulse than a single-photon continuous wave"
Actually, the so-called semi-classical approach to QED uses the classical energy density, 1/2(E*E + B*B) as an effective photon density. (This is discussed in Jackson's E&M text, and elsewhere I'm sure. The electric field associated with a photon, with vector potential, A(k,x)=a(k)exp(ikx-kt) + HC, where a(k) is a photon creation operator, is E = - dA(k,x,t)/dt, and is an operator. A great reference for all the gory details of photon fields and their associated operators and their interactions is Cohen-Tannaoudji,et al, Photons and Atoms; Introduction to QED.
* you cannot know ANYTHING about a photon between the time it is emitted and the time it is absorbed.
Although the concept of "thickness" is not strictly valid for a photon (which is not a solid physical object but an electromagnetic wave), one could characterize its thickness by its wavelength (i.e., if the size of a gap is about the size of a photon's wavelength, the photon will do funny things in trying to pass through the gap). For visible light, the wavelength is about 500 nanometers, or about 1/2000 of a millimeter. So when you see light reflected from a polished surface (metal or mirrored), the image has a thickness of about 500 nm. This becomes important if you have a very thin mirrored surface. If the mirror is thinner than 500 nm, then the "thickness" of the photon extends through the mirror, and the photon can actually travel through the mirror. This is an effect called "quantum tunneling".
A good case
can be made for the hypothesis that all photons are the same size and have
the same spatial distribution (energy density/energy) of mass-energy as
the electron.
(response) Not even close for most
photons wrt the spatial distribution of their wavefunction. The spatial
distribution for a radio wave photon's wavefunction can be as big as a
house or bigger.
Helical antennas
have the highest gain when their circumference is about the same as the
EM radiation wavelength. This leads one to believe that the spatial distribution
of EM radiation photons' wave is about the
same.
Take the case of a single photon of energy, 5 x 10^-6 ev (wavelength 21 cm) emitted by one hydrogen atom and absorbed by another. Your assumption is that it expands its mass-energy distribution from the size of one atom to about 42 cm and when it approaches the one atom that is going to absorb it is somehow able to shrink itself again to the size of that atom.
---------------------------------------------------------------
Wikipedia -photons
According
to the Standard Model of particle physics, photons are responsible for
producing all electric and magnetic fields,
The Maxwell theory predicts that the energy of a light wave depends only on its intensity, not on its frequency; nevertheless, several independent types of experiments show that the energy imparted by light to atoms depends only on the light's frequency, not on its intensity.
Einstein pointed out that many anomalous experiments could be explained if the energy of a Maxwellian light wave were localized into point-like quanta that move independently of one another, even if the wave itself is spread continuously over space.
The pivotal question was then: how to unify Maxwell's wave theory of light with its experimentally observed particle nature? The answer to this question occupied Albert Einstein for the rest of his life,[23] and was solved in quantum electrodynamics and its successor, the Standard Model.
However, experiments confirm that the photon is not a short pulse of electromagnetic radiation; it does not spread out as it propagates, nor does it divide when it encounters a beam splitter
Nevertheless, the photon is not a point-like particle whose trajectory is shaped probabilistically by the electromagnetic field, as conceived by Einstein and others; that hypothesis was also refuted by the photon-correlation experiments cited above.[28] According to our present understanding, the electromagnetic field itself is produced by photons, which in turn result from a local gauge symmetry and the laws of quantum field theory
In a classical wave picture, the slowing (of light in materials) can be explained by the light inducing electric polarization in the matter, the polarized matter radiating new light, and the new light interfering with the original light wave to form a delayed wave. In a particle picture, the slowing can instead be described as a blending of the photon with quantum excitations of the matter (quasi-particles such as phonons and excitons) to form a polariton; this polariton has a nonzero effective mass, which means that it cannot travel at c.
Much research has been devoted to applications of photons in the field of quantum optics.
Over 50 photon references
Online physics lecture
Photons are composed of probability ampitude waves not physical waves.
(this in relation to photons going down both legs of an interferometer
and (probably) double slit experiments)
Freely moving photon ( or particle) is simplest state. Photon wavelength
is the inverse of its momentum (p) scaled by planck's constant.
p = h/wavelength
Wave packets are just superpositons (additions) of a group of slightly
different momentum (frequencies) with a known average or peak value. For
a 'vast' number of frequencies this produces (in the limit) a single beat
note (single wave packet). This is what photons and electrons are.
wave packet with range of momentum 'delta p' will be spacially localized
in 'delta x)
and 'delta p' x 'delta x' > h/4 pi (uncertainty principle)
=====================================================================
Photons of light
That light
is quantized (quanta of light is called a photon) was figured out from
the photoelectric effect (& Compton effect). When light shines on certain
metals in a vacuum, electrons are released that can be captured, measured
and counted. This is the photoelectric effect.
Tests by Lenard & Millikan (starting in 1902) showed that the number and energy of electrons freed from a metal plate by light varies in an interesting, and surprising, way on the intensity and color (frequency) of the light. These results were hard to explain using the wave theory of light, which was very puzzling since the wave theory of light was well supported experimentally. All the known properties of light, such as reflection, diffraction and interference patterns had been shown in the 19th century to be explainable if light was a wave. Furthermore Maxwell in the 1860's had found that light was (very likely) an electromagnetic wave based on the fact that the calculated speed of electromagnetic waves (3 x 10^8 m/sec) closely matched the measured speed of light.
Photoelectric effect experiment
The simple
apparatus shown below, used by Lenard (& Millikan), generates free
electrons directly from light, allows the numbers of freed electrons to
be measured, and most importantly allows the kinetic energy of the freed
electrons to be accurately measured. Since the energy freeing the electrons
comes only from the light, measuring the electron energy provides information
about the light energy.
Lenard's (& Millikan's) photoelectric apparatus was a specialized cathode ray tube, a large, glass, vacuum tube with two electrodes. In the tube at one end (right) a metal plate (with a clean surface) was illuminated (through the glass) by bluish/white light from a very bright carbon arc light. The intensity of this light could be varied over a huge range (some refs say 1,000:1) by varying its current. At the other end of the tube (left) a 2nd metal electrode (not illuminated) collects the electrons that the light knocks off the surface of the plate.
The electrodes were connected together outside the tube via an amp meter and a battery connected through a variable resistance (variable voltage source). The material used for the illuminated plate was found to affect the results, so different metals were tested.
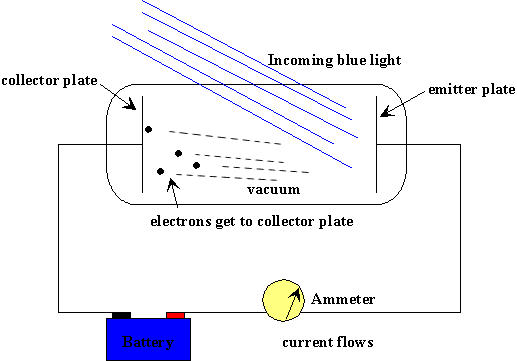
From a modern perspective this tube is a type of solar
cell. A voltage is generated between the electrodes due to the action of
light photons kicking electrons free from atoms on the metal plate's surface.
This tube can actually put out some power (if properly loaded) all of which
comes from the energy of the captured light photons.
A key feature of the experiment is that the voltage of the collecting electrode (relative to the illuminated electrode) can be adjusted. Since electrons have a negative charge, electrons are going 'uphill' from an energy viewpoint as they travel from the illuminated electrode to a negatively biased collecting electrode. The more negative the bias voltage the less the current until at some threshold voltage (which depends on material of the plate) it goes to zero. This 'zero current' threshold voltage is a direct measure of kinetic energy of the electrons released from the plate by the light.
The illuminated electrode develops a positive charge as it loses electrons that fly out into the vacuum. Externally if the connection between the electrodes is broken, the illuminated electrode is seen to develop a positive voltage of a few volts relative to the non-illuminated electrode. This open circuit voltage is another way to measure of the ev energy of the freed electrons. Connecting the amp meter between the electrodes (with battery voltage set at zero) allows the number of captured electrons to be measured. Adjusting the battery voltage to drive the illuminated electrode positive (equivalent to driving the non-illuminated electrode negative) reduces the current with the current going to zero at the open circuit voltage.
Photoelectric Java applet
Here is link
to a hands-on version of this classic experiment (with real values). (Java
must be installed in your brower for this to work.) You set the material
of the plate and adjust the voltage to find the current threshold. Note,
visible and ultraviolet light photons have energies of only a few electron
volts (ev) that is why it only takes a few volts to stop the current.
If it takes 2 volts to stop the current, then the fastest electrons emerged
from the plate with 2 ev of kinetic energy.
http://www.walter-fendt.de/ph14e/photoeffect.htm
Lenard's photoelectric results
The
freed electron energy was found to depend on the light frequency
minus the ev energy required extract them from the metal atoms, known as
the work function of the material. Surprisingly the energy of the
freed electrons was found to be independent of the intensity of the light..
Lenard found that the threshold voltage did not increase as the light got brighter, it stayed (about) the same, meaning the energy of the freed electrons was unchanging as the light got brighter. Since he could vary the intensity of his light something like 1000 to 1, this was pretty surprising. He did find, however, that a brighter light caused more electrons to be knocked out, as measured by a higher amp meter reading when the bias voltage was turned off. Hence conservation of energy is conserved. A brighter light beam has more energy because it has more (constant energy) photons, and these can knock out more (constant energy) electrons from the plate.
In 1902 almost nothing was known about the insides of atoms except that they appeared to contain electrons (& very likely) a balancing positive charge. But it was also known that some atoms, like radium, mysteriously gave out large amounts of energy when they decayed. Lenard concluded from his photoelectric studies that some (unknown) property of the atoms in the plate, not the light, was probably controlling the energy of the electrons kicked out. Maybe, he thought, his plate atoms were doing something like radium and putting out electron energy as they decayed. Here is how he put it in his 1906 Nobel address.
"I have also found that the (escape) velocity is independent of the ultraviolet light intensity, and thus concluded that the energy at escape does not come from the light at all, but from the interior of the particular atom. The light only has an initiating action, rather like that of the fuse in firing a loaded gun. I find this conclusion important since from it we learn that not only the atoms of radium contain reserves of energy, but also the atoms of the other elements; these too are capable of emitting radiation and in doing so perhaps completely break down." (Lenard 1906)Lenard also used various filters between his light source and the tube. This produced some weak evidence that the zero current threshold voltage (hence, electron energy) might increase with the frequency of the light, but it was not conclusive. Millikan in USA later confirmed that the electron energy did in fact increase linearly with increases in the frequency of the light. And it was found there was a threshold value for light frequency too (which varied with the material of the plate). Red light, even when very bright, produced no current, but very dim blue (or ultraviolet) light would produce a low current of high energy (high threshold voltage) electrons. It was all very puzzling.
In summary it was found that as long as the light frequency (color) was above a threshold value, experiments showed the energy of electrons knocked free was independent of light amplitude and increased linearly with light frequency. Lenard received the Noble prize for this (& other) work on 'cathode rays' in 1905.
How do you explain the photoelectic effect using the
wave theory of light?
The short
answer is, you can't.
If light is viewed, as it was at the time, as rapidly oscillating (non-quantized) electric (E) and magnetic (H) wave, then the following picture arises. The oscillating E field of the light wave would push and pull on the light, charged electrons in surface atoms causing them to start shaking and vibrating until some of them break free of the atom (and the surface). From this picture it would be expected that the higher the intensity of the light, meaning the higher amplitude of E field (at a particular frequency), the more violently the electrons would be shaken, and hence the faster they would be moving when they kicked free of the surface.
Therefore this simple, wave picture of light leads to a prediction that as the light brightness increased the measured energy of the freed electrons should increase. In the experiment this would be an increase in the zero current threshold voltage as the light brightened. But this is not what Lenard and Millikan found. They found the zero current threshold (freed electron energy) varied with the frequency of light and the type of metal in the plate, but did not vary as the light intensity changed. In other words the photoelectric effect was found to be inconsistent with the wave theory of light. Very puzzling.
I read Lenard's 1905 Nobel address. His explanation of the results of his photoelectric experiments was that the energy of the freed electrons (for some unknown reason) depended only on the material of the plate. (Lenard had only weak evidence that the energy of the freed electrons might vary with frequency of the light. Millikan a few years later showed that there was a linear relationship between the freed electron energy and light frequency.)Einstein's photoelectric theory
Out of Lenard's, Millikan's, and Einstein's work on the photoelectric effect came a very simple equation for the energy of light photons (below). (An equation that surprised me, when I first saw it in my physics textbook.) The energy of light photons is just a linear scaling of light frequency with the scaling constant being Plank's constant. Plank's had found this constant a few years earlier when he studied blackbody radiation and found that the electron radiators (as he saw it) in the blackbody material had to be quantized.
Energy of light = h × f
= h × c/wavelength
where
h = Planck's constant (6.626 × 10^-34 J·sec)
or (0.4136 x 10^-14 ev - sec)
Measuring planck's constant
Plank's constant
can be directly measured using the photoelectric apparatus (se above) and
varying the frequency of the light. The slope of energy vs light frequency
is Plank's constant (h). Here is Millikan's 1916 data showing the measured
electron energy from six colors falling on a nice straight line. As I eyeball
this curve, I find the slope to be (1 ev/ 2.4 x 10^14 hz) = 0.42 x 10^-14
ev - sec, which is very close to the modern value of 0.4136 x 10^-14. In
fact this method is an accurate way to measure Plank's constant, because
in this experiment Plank's constant is very exposed, being derivable from
measurements of only voltage (energy) and frequency.
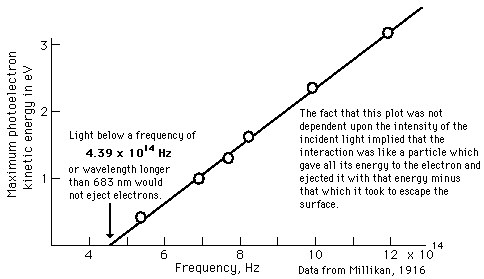
Repeating the experiment with different plate materials (cesium, potassium, and sodium are used in the applet above) also resulted in straight lines with the same slope as above (see also below), however, the zero energy (intercept) varies. This showed that the slope (Plank's constant) was a property of the radiation and the zero energy point (work function) was a property of the material. The slope of the above data turned out to be the same as the scaling constant Plank has proposed around 1900 to explain the coupling between matter and radiation in blackbodies, hence the name Plank's constant.
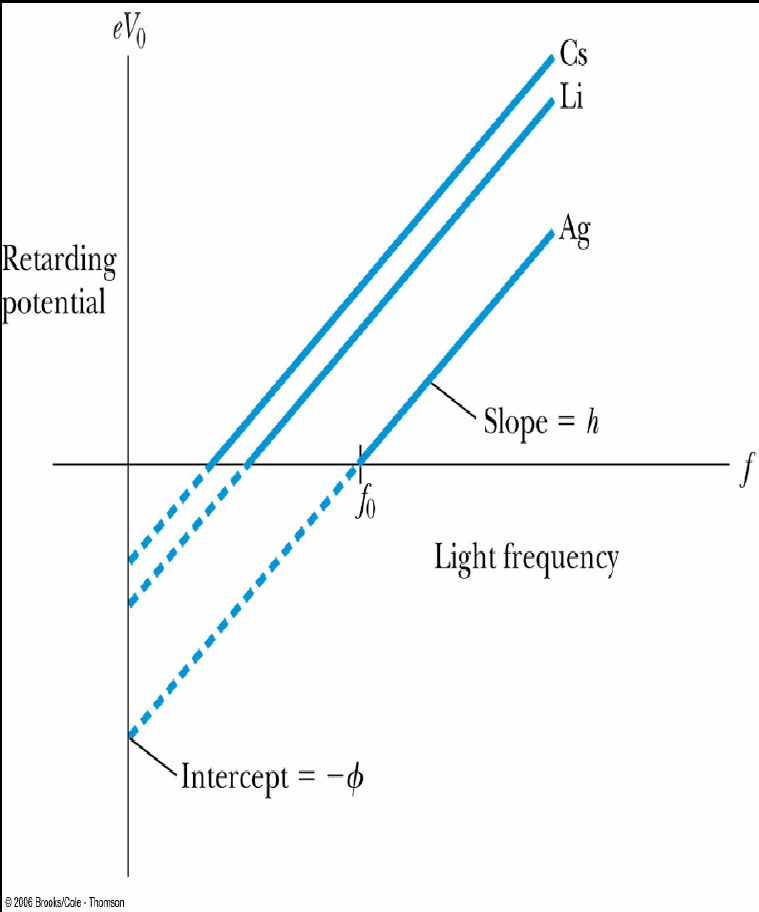
Photons couple to electrons in different ways depending on on the energy of the photon and whether the electron is bound or free. In the energy range of UV light (few ev) photons couple to electrons (primarily?) via photoelectric coupling. In this process the photon disappears and all the photon energy is transferred to the electron. Some the energy is 'used' to accelerate the electron out of the energy well it is in near the nucleus with the balance of the photon energy going into kinetic energy of the now freed moving electron. It is the kinetic energy of the moving electron that the experiment measures.
In the plot above the lines are extrapolated to an energy intercept at zero frequency. The negative ev of this intercept is the energy needed to free the electron (zero energy is a free electron) from its atom in that material. I found one reference that said the electrons kicked out via the photoelectric process are (always/mostly?) an electron from the inner orbit. Higher elements with larger positive charge hold the inner electrons more tightly. Notice above that silver has the deepest electron well. (However this is apparently not rigorously true since lithium is element three.) Note for the real data to fall on a straight line either the electrons must all come from the same orbit, or else the experimenters are averaging out the orbit energy variation.
Compton effect
The Compton effect
is electrons being deflected by X-ray (high energy photons) in the same
manner as two billiard balls colliding. This can only be explained if light
photons have a particle like nature.
Let's apply what we have learned about energy and mass to light. We know photons have energy, not only from the photoelectric effect, but you can feel you skin warming standing in bright sunlight. We know that (surprise) photons of light travel at the speed of light. Since there is energy to mass equivalence, photons must (in some sense) have mass.
But notice there is a problem if we try to apply our relativitistic mass formula (mo/{1 - (v/c)^2}^1/2) to photons. When v=c, the denometer goes to zero, so the result is mo x infinity. The only way have the energy be finite is for rest mass of a photon (mo) to be zero, which is true. However, multiplying zero x infinity is not good math.
The 'mass problem' for speed of light particles like the photon is circumvented by calulating their momentum instead. Classically momentum (p) is the mass x velocity (p = mv). Notice we can rewrite classical kinetic energy in terms of momentum.
E = 1/2 m v^2 or E = m v^2
E = 1/2 p v
or
p = 2E/v
This classical relationshiop between momentum (p) and energy looks like it might work for photons.
p (photon) = 2E (photon)/c
Momentum of photons can be measured by measuring the pressure of light.
Light from stars
In the
photosphere ("the sphere of visible light") atoms are "heated" by convection
and stimulated through refraction to vibrate at a rate slow enough to give
off visible light. In a sense the "refractive index" of the Sun's photosphere
is the means by which invisible (high energy) photons from inside the star
are converted into visible light.
Basics of light
http://fuse.pha.jhu.edu/~wpb/spectroscopy/basics.html
Units of light
http://fuse.pha.jhu.edu/~wpb/spectroscopy/units.html
Light magnetic and electric fields
(from book Integrated Photonics: Fundamentals
by Ginés Lifante, 2003) pages 31, 32, 33
for monocromatic plane EM waves light (pure sinewaves) says E and
H are in-phase (explicitly saying both peak at the same time) He shows
they both as sin(wt -kz).. This waveform is plane and linearly polarized
(in materials --- freq does not change,
but wavelength changes --OK)
However, you can add a pair of E and H cos waves too.... Now you have circularly
polarized
key points (for Ken Bigelow)
* in phase is for monocromatic light ----
pure sinewaves which can not be localized.
so my interpretation is no energy was sent!
* energy can perhaps be passed between polarizations
* in wave packet there are many frequencies. Whoses to say whats in phase
-----------------------------------------------
For
a wave moving right (along z axis) the electric field oscillated up/down
(in x direction) and the magnetic field oscillates front/back (in y direction).
This type with modulations perpendicular to the direction of motion is
known as a transverse wave. The two fields are in-phase in time,
meaning both go to zero at the same time and peak at the same time. Note
the frequence of the fields is from the source of the photons and
is unrelated to the speed of the photons. For radio photons the freqency
can be quite low ( 1 Mhz for AM radio). The electric field orientation
defines the axis of polarization.
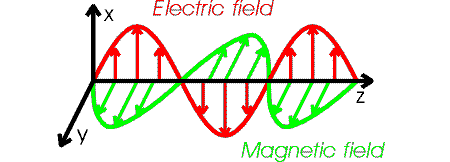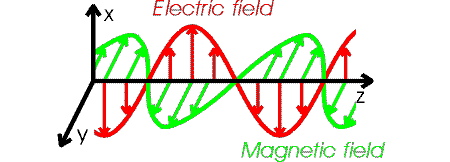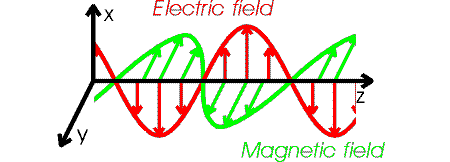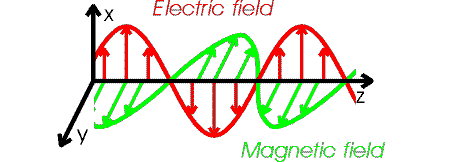
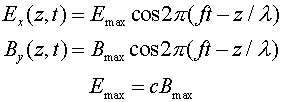
reference for above (Michigan State Univ lecture notes)
http://www.pa.msu.edu/courses/2000spring/PHY232/lectures/emwaves/maxwell.html
How do mirrors work?
Light makes
electrons wiggle and wiggling electrons make more light which cancels the
incoming light in the medium, but propagates back out of the surface according
to the law of reflection. Another way of saying it is elastic collision
with surface + momentum conservation leads to the law of reflection. (blumfeld0)
A curious thing --- mirrors generally seem to generally be treated as ideal devices, i.e. they absorb and reemit photons with zero delay. For example, the mirror clock in the relatitivty thought experiment clearely assumes zero delay for the 'bounce' of the photon off the miirror.
It seems unlikely (to me) that real mirrors would have zero delay when they reflect (absorb and reemit) a photon. I have read that real mirrors have some depth, i.e. the reflection does not occur exactly at the surface but in a skin depth that is related to some wavelenght (wave function). In fact, if the mirror is made thinner than the skin depth some of the light will leak through (tunnel through?).
Where do photons come from?
This
is an interesting question. I never see this written about, and when I
began writing this I did not know the answer. The simple answer appears
to be (nearly all) photons come from electrons. (Does this apply
to the sun??) A non-electron photon generator is annihilation of
matter and anti-matter. An electron can be attached to a single nucleus
(atoms) or in chemically bonded atoms (molecules) shared by several nuclei.
Electrons can be free (in vacuum), or they can be quasi-free, like in a
metal or semiconductor where they easily drift from atom to atom.
Photons are emitted (& absorbed) by free electrons that are accelerating or decelerating. An electron excited by incoming radiation can oscillate back and forth at (or near) the frequency of the incoming radiation. An electron oscillating back and forth is continually being accelerated. I suspect this type of electron photon emission explains light reflection and thermal heat radiation. Photons are also emitted by electrons in atoms when they change orbits or change their spin. The quantum nature of the atom restricts the allowable energy levels of photons generated by these processes, so this type of radiation tends to occur at discrete frequencies. The famous 21 cm hydrogen line of cosmology is a photon emission due to a spin change.
Wave Packets
Quantum theory
says photons, electrons, etc can be describes as 'wave packets'. It's (sort
of) an evelope with a sinewave inside. It's really nothing more than a
sum (superposition) of sinewaves of slightly different frequency.
Textbooks derive this starting with the sum of two (equal amplitude) sinewave
of sligltly different frequency. When plotted you see repeated beats notes
(at differece frequency). Extended to five sinewave you begin to see more
of a pulse envelope taking place {looks like sin(x/)x} In the limit
of a "vast number" of sinewaves of different frequencies and (I'm) pretty
sure carefully selected amplitudes you get a single envelope.
In other words a 'typical' photon with a finite mementum/frequency envelope has in it many different frequences. This what a photon from the sun looks like? How well you can localize the photon depends on the range of frequencies that it contains. A wide range of frequencies then you can locate it well, a narrow range of frequencies and you can't. For mono-chramatic light, which is a pure sinewave (no uncertainty in energy), a photon is everywhere in space (& probably in time too) . This explains this a physics forum answer --- If your hypothetical photon is monochromatic, then its wave function is a plane wave, not a Gaussian and its "width" can be practically infinite (size of the universe).
(delta p) x (delta x) > h/4 pi
Here are my (first draft) sketches of wave packets
(mostly a rehash of online lectures)
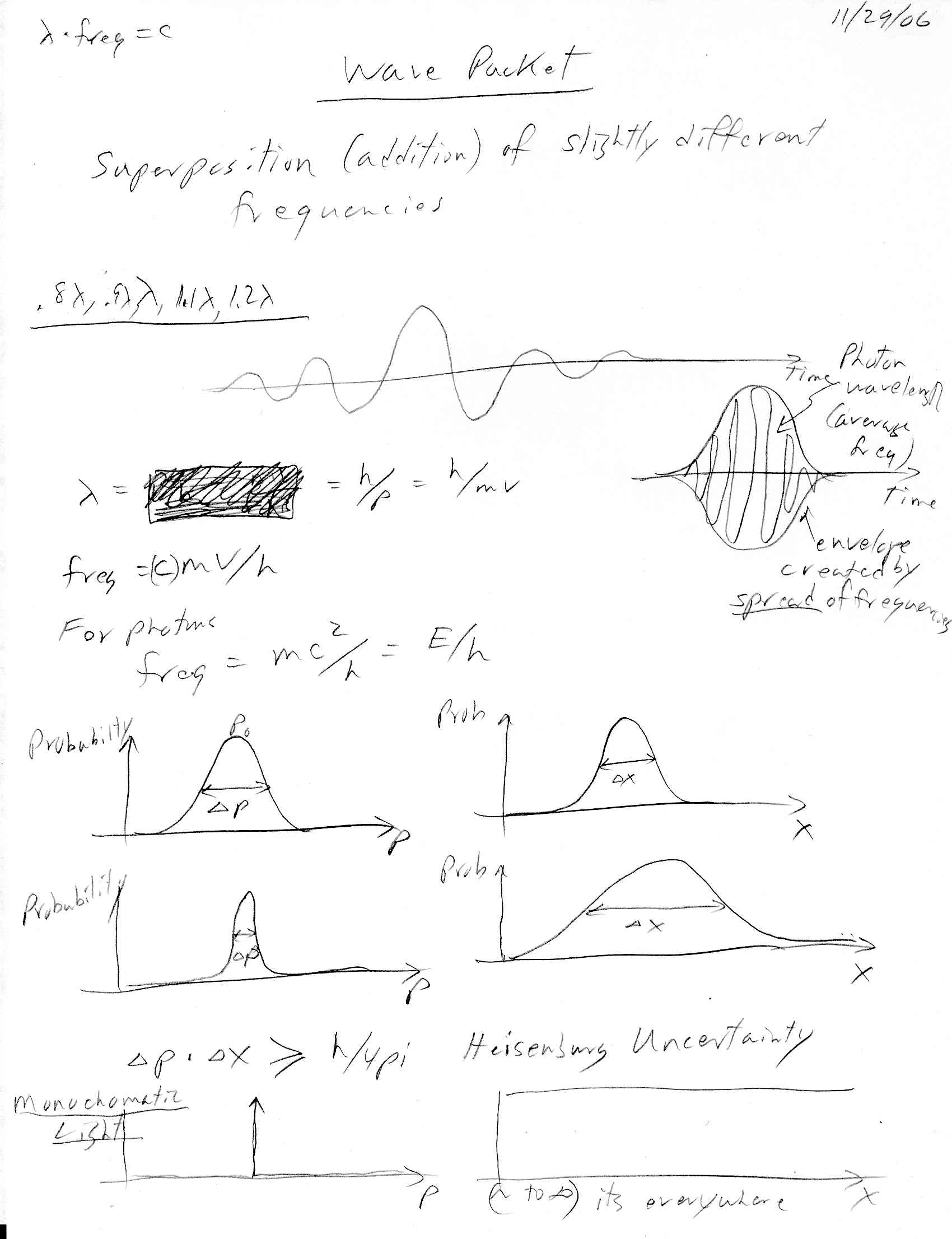
=======================================================
References
Charge of
an electron = 1.6 x 10^-19 coulomb
Mass of an
electron = 9.1 x 10^-31 kg
angstrom
= 10^–10 meter
==================================================================
Phony photon
(another oddball
paper along the lines of the Russian tuned antenna.)
The key argument is that it is atoms, acting as half wave dipole antenna receivers, which introduces the quantization. The field is not quantized. Harries simple, but effective, argument is this:
If you always use a volt meter with 1 mv resolution to measure voltage, voltage will appear to have mv quantization to you!These arguments are very interesting and I a lot of sympathy for this type of argument. Photons are real squishy, and when it comes to describing photons 'in flight' phyicists just thow up their hands, saying it is unknowable.
The key here is antenna theory. Antenna theory is complicated, mostly not understood even by electrical engineers. I doubt physicists have any real understanding of antennas. So it could be argued that 'photons' are a (too) simplistic explanation for radiation reception arrived at by people who had no understanding of the complicated real aspects that are known to be true at lower (radio) frequencies.
Here an electrical engineer (Geoff Harries, who apparently is also a hi-tech fiction author) argues that light (and all electric radiation) is a non-quantized wave. Rather it is the atom as a receiver that is quantized, acting like a half wave dipole. This argument rests on antenna theory and extrapolates from known engineering of antenna to higher frequency where atoms are the antenna.
His tutorial section has good simple, nearly all text, explanations. In 30 min of reading it looked accurate. He is able to explain antennas simply. He goes over in detail photoelectric effect, compton effect, much more.
http://www.the-phoney-photon.com/
Con: He does not seem to address the strongest argument
I have seen for photons: When a very weak (photoelectric) field is turned
on, some electrons come out immediately. Calculated time for the field
to transfer energy by classical means is much longer than measured times.
The key here would be how this calculation is done.
====================================================================================
Neutrinos faster than 'c? (11/18/11)
Physics in
action, in real time.
Overview
A neutrino
experiment in Sept 2011 by CERN and a neutrino lab (see picture of neutrino
detector below) deep in the Gran Sasso mountain of Italy 454 miles away
found that neutrinos arrived just slightly faster than the supposed 'universal
speed limit' of 'c' (3 x 10^8 m/sec, or about 1 usec/thousand feet). The
difference was tiny 58 nsec faster than the expected time of flight (direct
through earth from CERN to detector in Italy) of about 2,400 usec. This
is faster than 'c' by 0.0024%.

View of the neutrino 'Oscillation Project with Emulsion-Racking
Apparatus' detector (OPERA)
at the Gran Sasso National Laboratory (LNGS) located
under the Gran Sasso mountain in Italy, Nov. 14, 2011 (Getty)
This large scale experiment (160 physicists involved) reported the f'aster than light' result with a high confidence (high sigma). But of course you can't correct for systematic errors not recognized, and initially most people expected such a systematic error would be found. Firstly, since light travels about 1 nsec/ft, a 58nsec deviation could be explained by an error of just 58 ft in 454 miles distance between CERN and the neutrino lab. Another issue is that the neutrino pulses generated by CERN were much wider than 58 nsec (10 usec pulse width), so a bunch of statistical analysis was needed to even say broad pulse is 58 nsec off. But after two months, and many many suggestions from outside, the CERN team has been unable to explain it away.
Nov 18, 2011 update
Drudge is
reporting today a 2nd test by the Italians has confirmed the 'faster than
light' measurement of neutrinos. Getting interesting. The 2nd test two
months later by the same labs addressed the latter issue of a 'too wide'
pulse by really narrowing the CERN generated neutrino pulse. Later in day
NYT reports in the new test the pulse width was only 3 nsec, far shorter
than the discrepancy, which totally removes pulse width as an explanation
for a faster than light result. In this new test the neutrinos were measured
as arriving 62 nsec early, which since the pulse width is so short is likely
a more accurate number than the first test, and can be considered a confirmation.
If (if!) distance between CERN generator and detector in Italy is right,
this is faster than speed of light by (62 nsec/2.4 msec) or 0.0026%.
Link to the 32 page CERN preprint paper (dated 17 Nov 2011) discussing the test results is below. Title: Measurement of the neutrino velocity with the OPERA detector in the CNGS beam. I count about 189 authors on the title page!
http://arxiv.org/pdf/1109.4897v2
In comments to the CBS/Drudge story today I saw some engineers were making the case the neutrino test might be measuring 'true c". I have long studied how cable L,C slows down a voltage edge, and wrote two years ago (2009) in this essay that maybe space LC (due to virtual particles) might be doing the same thing, but aside for a couple of references no physicist ever seems to have looked at this seriously. I added in my 2 cents to the discussion by posting to the CBS news story the following comment:
" Exactly right. The propagation time of electrical pulses down long cables can be modeled and calculated using the capacitance and inductance of the cable. Space has virtual charged particles for the E,H fields of light to react with. As an EE power engineer, I have long thought the L,C cable model of wavefront propagation (speed about c/2) to be a good analog for how the virtual particles of a vacuum might slow down light. It may very well be that the neutrino test is measuring 'true c', or very close to true c. No physics revolution would be required. Just a recognition that space's (cable-like) L,C properties always slightly slows down light from true c."So is 'true c' the real speed of light?
Posted comment 11/18/11 to CBS (Drudge ref) news story on 2nd confirming test
Obviously all this needs
to be considered most likely an experimental error until another lab can
confirm it. But as one physicist said neutrinos are weird (it was only
fairly recently they were found to have some mass), so it's possible. Wild
stuff.