Special Relativity
-------------------------
created 9/06
revised 11/4/13
Go to homepage
Relativity introduction
Special
relativity postulates that all laws of physics, including the value measured
for the speed of light, are exactly the same for all observers who
are moving at constant speeds relative to each other. The implication of
this is that the time is not the same for all observers. Special relativity
provides a fundamental understanding of what otherwise appears to be difficult
to understand (if not bizarre) experimental results:
* You can't get particles to go faster than 3x10^8 m/sec regardless of
how much
energy you give them.
* You can increase the energy (apparently without limit) carried by particles
moving
near 3x10^8 m/sec even though they barely go any faster.
*
When light is emitted from a moving source, the speed of the source is
not added
to (nor does it have any effect on) the speed of the emitted light without
need
for a stationary medium (ether) to carry the light.
* High speed, unstable particles (muons) with only 2 usec lifetimes, created
in the
upper atmosphere by cosmic rays, are (somehow) able to hit the ground in
large
numbers even though their with short lifetimes they should almost all decay
high in the atmosphere.
As a bonus, special relativity explains that mass and
energy are (in some sense) equivalent and that a magnetic field is just
a relativistic artifact of the electric field from moving electrons.
Four relativistic concepts from just two experiments
(2/10/11)
1) Acceleration of electrons with high voltage
Classical
physics predicts that electrons should be able to be accelerated to any
speed, limited only by how much voltage is available, but tests show (see
below) this is not true. What happens is that at a fairly modest voltage,
as electron speeds approach [c = 3 x 10^8 m/sec], the speed curve begins
to flatten and no amount of energy can accelerate the electrons above this
speed limit.
Thermal measurements
show that the energy carried by the moving electrons does not flatten and
can (apparently) be increased without limit. Higher acceleration voltages
drive the (kinetic) energy carried by the electrons higher and higher even
though speeds near 'c' barely change. Classical physics has no explanation
for this.
2) Short lifetime muons travel all the way through the atmosphere
Muons
(heavy, unstable electron-like subatomic particles) are continually created
in the upper atmosphere by fast moving cosmic rays (mostly protons). Muons
are unstable with a measured lifetime of 2 usec (round numbers). Since
the fastest any particle can move is 'c' (1 nsec/ft or 1 usec/thousand
feet), travel time from 50,000 feet to the ground is (at least) 50 usec.
This is 25 muon lifetimes, so classical physics would predict that only
a tiny fraction of muons would survive long enough to reach the ground,
but this is not what tests show. What is found is that a substantial fraction
of the muons are (somehow) able to survive long enough to travel all the
way through the atmosphere and reach the ground.
(update)
'Hyperphysics'
site (using slightly different numbers, which it says agree with historical
muon experiments) calculates that about 5% of muons created 6 miles up
(10 km) and traveling only at .98c will reach the ground, vs less than
1 in a million for no time dilation, so muon time dilation is NOT a subtle
effect.
These two simple
experiments demonstrate something very strange happens as objects approach
[3 x 10^8 m/sec], which is known to be the speed of light in a vacuum.
In fact they demonstrate all four key relativistic concepts: hard speed
limit, mass increase, time dilation and length contraction. The 'relativistic
correction factor' is the same for all three parameters: [1/sqrt{1 - (v/c)^2}],
which is 1.41 at 70.7% speed of light.
Hard speed limit
Electron velocity
is seen to flatten and limit at [3 x 10^8 m/sec], the speed of light ('c'),
even though the acceleration voltage though which they travel is raised
higher and higher. This should pump more energy into the electrons, and
thermal measurements show it does, but still the speed barely increases.
Very weird, but it's an experimental fact, this is how mother nature is!
Increase in mass
Measurement of the
heat generated by crashing high speed electrons into a barrier confirms
that even though the speed limits at the speed of light, the energy carried
by moving electrons does not limit and can (apparently) be increased without
limit. So if velocity near 'c' can barely increase, how can the kinetic
energy, which is classically [KE = (1/2) m v^2], increase? The special
relativity explanation is that the as 'v' begins to flatten out 'm' begins
to increase, multiplied by the relativity factor. (For v = 99.92%c mass
increase is x25).
Muon penetration through atmosphere
(In
round numbers and simplified physics) measured lifetime of a muons is 2
usec. Muons are continually created in the upper atmosphere traveling at
speed near 'c'. In classical physics muon's traveling near 'c' would
be expected to penetrate only about 2,000 feet (@ c = 1 nsec/foot or 1,000
ft/usec) into the atmosphere, but instead a significant fraction of muons
penetrate all the way to the ground (approx 50,000 ft or 10 miles).
Time dilation
From the point
of view of earthmen the logical explanation for this is that moving muons
appear to have a stretched out decay time, and in fact an adjustment to
muon time is the relativistic explanation. The period of the clock on a
moving muon as measured from earth is seen to be increased by the relativity
factor (x25 idealized). Time on a moving object is seen to be dilated.
Length contraction
Muon men agree
that the muons are hitting the ground, but they don't agree with the earthmen
as to why. They do not agree that the muon clock is running slow.
When they measure the muon decay time, it is 2 usec like always. So what
relativistically has changed for them? It's the thickness of the earth's
atmosphere. From their perspective the moving earth with its atmosphere
is rushing at them with a speed near 'c', and the muon men see it squashed,
here by a factor of x25 (from 50,000 ft to 2,000 ft), so of course they
can make it through a 2,000 ft thick atmosphere and hit the ground before
decaying. The length of a fast moving object (along its direction of motion)
is seen to be contracted.
Visualizing time dilation
Below I sketch
how a muon light clock would look to muon men (left) and earthmen (center).
A light clock is a photon bouncing back and forth between two mirrors.
In special relativity everybody measures the speed of a photon as 'c'.
Muon men just see the photon bouncing back and forth. To keep the numbers
simple let's say the (muon) mirrors are 1,000 ft apart, then a muon man
counts two tick (2 usec) before the muon decays. The earthmen can clearly
see the clock make two ticks too, yet from the shape of the photon path
it is clear to them that the clock is running slow compared to what muon
men will see.
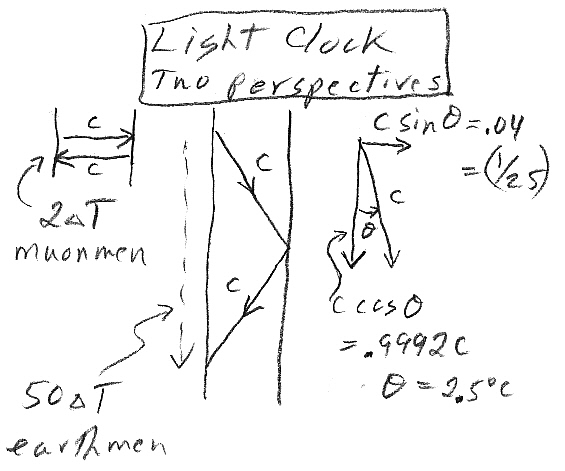
Muon men (left) see two (1 usec) ticks before decay.
Earthmen (center) same as muon men also see two ticks
of the light clock,
but due to mostly downward travel of photon (@ c)
from their perspective the two ticks take 50 usec
allowing the muon to travel 50,000 feet down through
the atmosphere (@ 99.92% c).
In other words
the earth men's explanation for the muon experiment results is that they
'see' (experience) time on the moving muons as slowed (time dilation),
while the muon men's explanation is that they see the thickness of the
atmosphere rushing at them as compressed (length contraction).
Speed of light --- nature's speed limit
Acceleration
tests on electrons done over 50 years ago showed that as the accelerating
voltage increased the speed initially increased as the square root of energy,
which is consistent with Newtonian mechanics where [kinetic energy = 1/2
m vel^2]. However, a strange thing happened as the speed neared 3
x 10^8 m/sec. The speed increases got smaller and smaller, until finally
no amount of energy could get them to go any faster. The speed at which
the electrons maxed out in the lab (3 x 10^8 m/sec) is equal to the speed
of light in a vacuum. Bizare indeed.
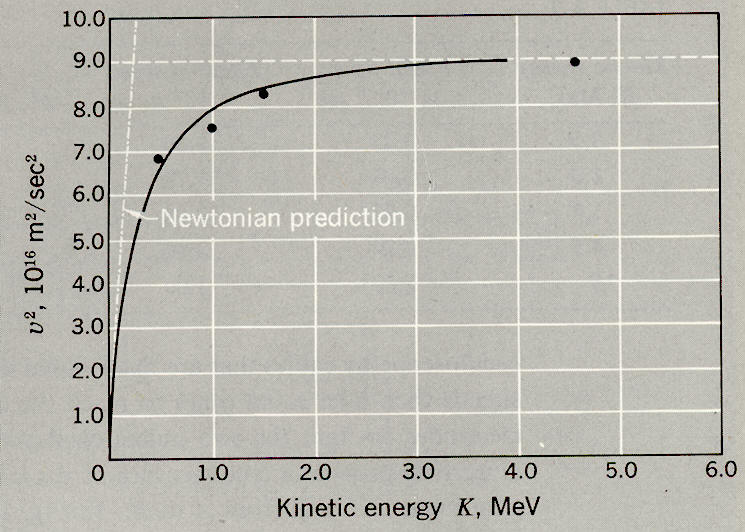
Does mass increase with speed?
As the voltage
of the machine increased, the heat measurement of the electrons hitting
the target showed that the electrons were indeed carrying all the energy
applied. How is this possible if the speed is barely increasing? Well,
there is another term in the kinetic energy equation (E = 1/2 m vel^2)
and that's mass. The almost inescapable conclusion is that at speeds near
the speed of light the electron mass must be increasing, and it must be
increasing in proportion to the increases in electron energy. As energy
goes into the electrons (Energy ==> mass), and when the electrons
hit the barrier (mass ==> energy) in the form of heat.
What's the
formula for how mass increases with speed? Well, the relativistic
'fudge factor' for both time dilation and length contraction is 1/sqrt{1
- (v/c)^2}. Let's try it with mass and see how it works out. 1/sqrt{1 -
(v/c)^2} goes from one at zero speed to larger and larger values as speed
approaches the speed of light. We want mass to increase with speed, so
we multiply the (rest) mass by the relativity factor. In the equation below
the rest mass (normal, low speed mass) is represented by the symbol 'mo'.
guess
m = mo x 1/sqrt{1 - (v/c)^2} = mo x {1 - (v/c)^2}^-1/2
Since (v/c)^2 is always less than 1, we can expand this
formula into a power series and as long as speeds are moderately below
the speed of light only the first two terms are significant.
power series
(1 - a)^-1/2 = 1 + 1/2 a + higher order terms
set
a = (v/c)^2
then
m = mo + 1/2 mo (v/c)^2
multiply by c^2
m c^2 = mo c^2 + 1/2 mo v^2
This looks encouraging. If m c^2 is interpreted as relativistic energy,
then at low speeds we find it is equal to 1/2 mo v^2, which is just
Newtonian kinetic energy, plus a constant term (mo c^2). In classical
mechanics when we lift or drop or apply force to an object we only are
concerned with changes in energy, so if mass did have constant
energy associated with it it would never be noticed! The constant
term (moc^2) is very large since it is mass multiplied by the speed of
light squared. How can we interpret this term? Well, it's called the rest
mass energy and it's famous.
1/2 mo v^2 => classical kinetic energy
mo c^2 => rest mass
energy
I think we made a good guess for the formula of mass vs speed. At low speeds
it is compatible with classical mechanics, and at high speeds it agrees
with experiment. Here's data showing how mass of electrons increases as
their speed nears the speed of light. The smooth line is supposed to be
m/mo = 1/sqrt{1 - (v/c)^2}. Let's check it at v/c=0.9 to be sure.
With v/c = 0.9 m/mo = 1/sqrt{1 - 0.81} = 1/0.436 = 2.29, which agrees
with the plotted smooth curve.
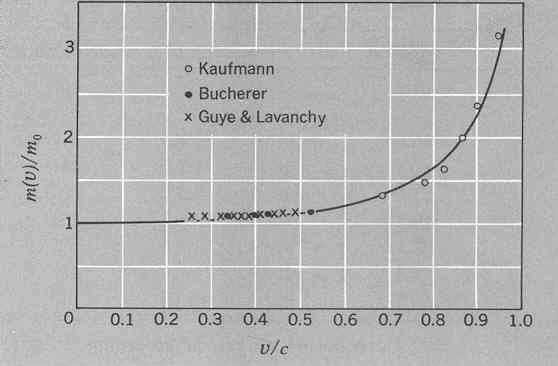
Inertial mass of electrons vs speed. Special Relativity
by A.P. French, MIT Introductory Physics Series, 1968
Mass as c is approached (update)
So how does
mass increase up near the speed of light? We take the formula above and
plug in v = (c - delta), where delta is a small fraction of c, for example
for v = .9c delta = .1c and for v = .99c delta = .01c.
(v/c)^2 = ((c - delta)/c)^2 = (1 - delta/c)^2 = 1 - 2 delta/c + (delta^2
term than we can neglect)
[1 - (v/c)^2] = 1 - (1 - 2 delta/c) = 2 delta/c
m = mo x 1/sqrt{1 - (v/c)^2}
m = mo x 1/sqrt{2 delta/c} = mo x sqrt{c/2 delta}
For delta = .1c m = sqrt{5}
For delta = .01c m = sqrt{50}
So the mass goes up as the 1/2 square root of the delta
of the speed below c.
E=m c^2
Notice the
constant rest mass energy term (mo c^2) that has popped out of our (assumed)
relativistic energy equation is the famous Einstein equation E=m c^2.
It
is a prediction of relativity that mass <=> energy, more
specifically that:
Mass
(scaled by c^2) is (somehow) equivalent to energy
It took a while
for all the implications of this equivalence between mass and energy to
be understood, but it turned out to be a key to understanding atomic fission,
fusion, and radioactive decay. Here we have one of the most famous equations
in physics (E=m c^2), and by just extrapolating from experiments
with accelerated electrons we found it. Pretty damn good.
Time dilation and length contraction
When the equations
are worked out for how you 'see' a moving body (moving at a fixed speed
relative to you) you see it affected by two strange 'distortions' that
are generally called time dilation and length contraction. These
are not illusions, but real effects demonstrable by experiment. These effects
result because the only information you get from a moving body (in the
form of light) travels at a fixed speed, speed of light. A spaceman
sitting on a moving body also 'sees' us affected by time dilation
and length contraction. Einstein explained all this by showing how the
speed of light limit means that we and a moving spaceman will not agree
on whether events we both see are simultaneous. In other words we don't
have the same time!
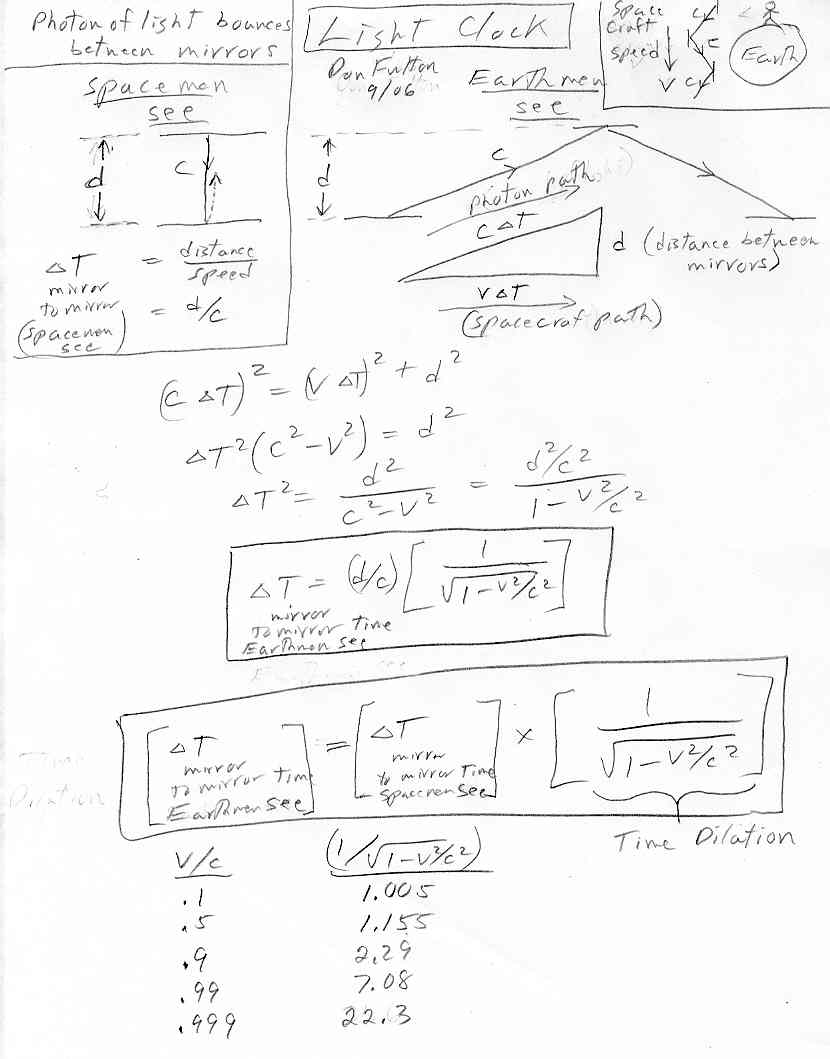
Time dilation
Probably the
easiest way to calculate, and visualize, time dilation is with a light
clock.. A light clock is an idealize, simple clock that is just a single
light photon bouncing back and forth continuously between two parallel
mirrors.
Suppose the
light clock is on a spacecraft that goes zipping by the earth at speed
v.
(Technically v is the relative speed between the frame
of
the earth and the frame of the spacecraft). The light clock is oriented
so the photon is bouncing up & down perpendicular to the direction
of motion of the spacecraft. Earthmen measure the same distance between
mirrors as the spacemen because the (Lorenz) contraction of the spacecraft
is only along the axis of motion. Whereas the spacement see the light photon
just bouncing up and down, the earthmen see the photon moving diagonally,
the combination of the up/down motion and the forward motion of the spacecraft.
The notes below
calculate the photon time to travel mirror to mirror time as calculated
by the spaceman and the earthman. For the spacemen the calculation is extremely
simple:
Mirror to mirror time = (distance between mirrors)/(speed of light)
(spacemen see) = d/c
For the earthmen
the photon diagonal distance between mirrors is the hypotenuse of a right
triangle. Since the photon always moves (as measured by everyone) at the
speed of light (c), the distance it moves along the diagonal in
time delta t is {c x delta t}. The base of the triangle is the distance
covered by the spacecraft while the photon is traveling between mirror
{v x delta t}. The height of the triangle is the distance between
the mirrors (d). The earthmen calculate the time it takes the photon
to diagonally travel between mirrors {delta t} by using Pythagorean
theorem, known since Greek times, which is the square of the hypotenuse
is equal to the sum of the squares of the other two sides. The result (see
the notes below for the details) is
Mirror to mirror
time = (d/c) x (1/sq root [1 - (v/c)^2])
(earthmen see)
= Mirror to mirror time x (1/sq root [1 - (v/c)^2])
(spacement see)
As the
spacecraft speed gets close to the speed of light, the term (1/sq root
{1 - (v/c)^2}) begins to grow larger than 1. At 90% of the speed
of light it is 2.29 and at 99% the speed of light 7.08. The earthmen measure
the period of the fast moving clock to be longer, i.e. the clock running
slow, compared to the spacemen traveling with the clock. This phenomena
is known as time dilation.
Length contraction
Sitting
on a high speed muon coming through the atmosphere (see next section) your
explanation of why so many muons survive to hit the ground is that the
atmosphere (& the whole earth) looks flatted out like a pancake.
It is contracted
in the direction of motion. So what's the formula
for contraction? We know it already. Consider, if earthmen see the
muon clock running slow by the factor n, then the spacemen must
see the atmosphere thinned by exactly the same factor n. The
factor for length contraction (in the direction of motion) has to be just
the inverse
of factor for time dilation. Inverse because the increased
period of the high speed muon clock translates to a decreased length
of the atmosphere as seen by muon.
Length
= Length
x sq root [1 - (v/c)^2]
(spacemen see) (earthmen see)
How to remember time dilation and length contraction
The
math of Einstein's special theory of relativity is very simple, a little
trigonometry and simple algebra. The concept of simultaneous events is
tricky conceptually. But hardest (for me) to keep straight always has always
been: who is seeing what time dilate, who is seeing what length contract,
etc.
Trick --- Remember excess muons from cosmic
rays survive to hit the ground. From earth's viewpoint the reason is that
the muons are decaying more slowly than normal (time dilation), but from
a muon spaceman's point of view the reason is that the atmosphere looks
thin (length contraction).
Muons
are created high up in the atmosphere (10 miles) by cosmic rays (high speed
protons) hitting air molecules, and then travel downward through the atmosphere
at near the speed of light . Muons have a short lifetime of about 2 usec
(half life) as measured in the lab. At the speed of light it takes about
1 usec to travel 1,000 ft (300 m). In 1941 an experiment was conducted
where atmospheric muons were counted at the top of a 6,000 ft mountain
(Mt Washington) and at sea level. In the 6 usec it takes the muons to travel
6,000 feet wouldn't you expect that only (1/2)^3 = 1/8 of them would
survive? Well, that's not what the data shows. The 1941 experiment
found the sea level count was 72% of the mountain top count. Somehow
most
of the muons survive the 6,000 foot, 6 usec trip, almost six times (72%/12.5%)
more than would naively be expected.
Our explanation
from the ground is that we expect to see things happening slowly on a fast
moving particle. because we see their clocks running slow. We say their
time
is dilated. Therefore we expect it will take longer than
normal
(i.e. what we measure in the lab) for a high speed muon to decay. That's
our explanation as to why so many muons hit the ground.
Let's consider
the situation from the muon's point of view. Imagine you're sitting
on the muon. What do you see?
On
the muon you can consider yourself not moving and that the earth
is rushing up at you at nearly the speed of light. When you measure the
muons' half life (in your muon lab), it looks normal to you at 2 usec.
Yet you too see you have a good chance of hitting the ground.
Sitting on
the muon your explanation for hitting the ground is that the earth looks
flattened into a pancake. Side to side normal, but front to back contracted,
i.e. you see it contracted (only) along the direction in which
you see it moving. Looking from the muon the thickness of the
atmosphere (from creation of the muon to hitting the ground) it's much
less than 10 miles, Mt Washington looks to guys on muons to be less than
1,000 ft high. So from the muon point of view, the reason a lot of muons
survive to hit the ground with 2 usec half lives is that the atmosphere
looks thin, it's
length has been contracted.
Let's apply what
we've learned to a space ship that goes zooming by the earth. From the
earth we see the people moving around on the space ship slowly and the
space ship is shortened front to back.
Here's two references on excess muons hitting the ground.
http://www.prestoncoll.ac.uk/cosmic/muoncalctext.htm
http://web.mit.edu/8.13/www/JLExperiments/JLExp14.pdf#search=%22plot%20speed%20vs%20voltage%20%22speed%20of%20light%22%20%20accelerator%22
Time dilation and length contraction -- in particle
physics (update 4/11)
It turns out
that special relativity applies to subatomic particle collisions too. The
memory picture here is like the earth/muon picture except the high speed
muon is replaced by a high speed electron, and the flattened earth/atmosphere
is replaced by a flatten proton.
I recently
came across a striking picture from particle physics that allows visualization
of simultaneous length contraction and time dilation. It is in a
new technical biography about Feynman called, 'Quantum Man'. The SLAC particle
accelerator (still operating) accelerates electrons to very high speed
down a two mile straight path and collides them with protons. Feynman realized
that length contraction and time dilation view of the proton, as seen by
a high speed incoming electron, drastically simplified calculations of
the interaction of the electron with (possible) proton components, then
known as partons, soon to be called quarks.
The incoming
electron sees the proton flattened to a pancake, and if the proton has
charged subcomponents (partons), their motion would be seen to be nearly
frozen by time dilation, thus allowing the partons to be treated as independent.
The proton pancake shape is because the electron sees length contraction
along the direction of motion. Within the pancake shaped proton, in a plane
perpendicular to the direction of electron motion, any subcomponents the
proton has would be seen moving very slowly due to time dilation.
Proton as seen by high speed SLAC electron
High speed
(SLAC) electrons 'see' (and collide with) ---- pancake shaped protons that
each contain three barely moving charged subcomponents (quarks).
The 'scaling'
rule Feynman derived for this collision was that the electron/proton interaction
depended on the momentum of the proton's three constituent quarks and their
electric charge squared (p298). This explained a regularity seen in the
SLAC data and was one of the first indications that protons had an internal
structure.
Time dilation and length contraction --- Is that all
there is to it?
Unfortunately,
no. Just applying time dilation and length contraction sometimes gives
the right answer, and sometimes it doesn't! This is what makes understanding
special relativity so difficult. You think you understand, and then the
next problem you try to solve, you can't.
Here is one
of the keys --- When it comes to time, what you see depends on two effects:
time dilation and the doppler effect. If you are not moving (or can
consider that your not moving), then you always 'know' that any clock
on a moving (at constant speed) body is running slow, in other words, time
dilation always applies. The doppler effect, however, only applies
sometimes,
it applies when you are directly observing frequency or period of light
from (or to?) a moving body. So if you observe the effect of a slowed clock
indirectly, like how long (on average) does it take a muon to decay, then
time dilation is (often) all that is needed. But if (by some means) you
'look at' or 'track' how a moving clock is beating, you need to apply both
time dilation and doppler effect to solve the problem.
A simple way to figure what you see when a moving body
is emitting light
a) Time dilation affects when, or in what rate, the light is emitted
b) Doppler affects how the emitted light is seen. (The light can
be visualized in
space traveling at c and the observer is traveling toward or away from
the light at some fraction of c.)
So if the emitted
light is in the form of light pulses (or light frequency) controlled by
the clock on the moving body, then you apply time dilation to slow the
clock and figure what effect this has on when or how the light is emitted,
then you use the doppler effect to see how the emitted light (its period
or frequency) is affected by its velocity relative to the non-moving observer.
Doppler effect
Does
the speed of a light source have any effect on (or how your see) the emitted
light? The answer is yes. The speed of the emitted light is
not affected (a key relativity concept), but you do see the frequency
(or
period) and energy of the emitted light to be affected by the speed of
its source. This frequency/period/energy change in the light due to the
relative velocity between the source of the light and the observer is known
as the doppler effect. The doppler effect is used by astronomers
to measure (line of sight) velocity of astronomical objects relative to
the earth. This is done by measuring how much the frequency of prominent
spectral absorption lines are shifted relative to the same lines measured
in the lab.
Period is the
inverse of frequency, so if a moving light source is putting out light
in the form of pulses, then the doppler effect causes the measured time
between pulses to change, decreasing when the source is moving toward the
observer, and increasing when the source is moving away. Note doppler is
a separate effect from time dilation and is a stronger effect than
time dilation. Doppler is a first order effect {(1+/-v/c) or 1/(1 +/- v/c)}
whereas time dilation is a second order effect {sqrt(1 - (v/c)^2)}.
In summary,
the timing of light pulses controlled by a clock on a moving source are
seen by (inertial) observers to have two sources of variation: relativistic
time dilation and doppler effect. To find the timing seen by the (inertial)
observers multiply the the local moving clock timing by both the time dilation
multiplier and doppler effect multiplier.
1) relativistic time dilation multiplier --- always slows a
moving clock, increasing
the time between clock beats by the factor (1/sqrt{1 - (v/c)^2}.
2) doppler effect multiplier --- changes the time between clock beats
by the factor
(1 +/- v /c), so depending on the sign of v the time between clock beats
can
increase or decrease.
Note the doppler
effect is very asymmetrical. For high speed particles, as v approaches
c, (1 + v/c) approaches (1 + 1) = 2, but (1-v/c) approaches (1-1) = 0.
So if a fast moving body is moving away from the observer, time between
its emitted light pules can (at most) be seen to double. On the
other hand when a fast moving body is moving inward toward the observer,
time between its emitted light pulses can be seen to shrink nearly to
zero, so that the emitted light pulses arrive very close together.
Introduction to the twin paradox problem
I have read
about the twin paradox special relativity problem in two books and researched
it online. This problem in relativity is over a hundred years old. It was
referred to by Einstein in his original 1905 paper, and the formulation
involving twins and rockets ships is due to Langevin from 1911. Here is
the full version of the problem:
One
twin gets on a rocket ship and travels to a nearby star at near the speed
of light and immediately returns to earth at the same high speed, while
the other twin remains on earth. Both twins are able to track the clock
(time) of the other because they each flash a light based on the beats
of their local clock. When the traveling twin returns home and the twins
are reunited, the traveling twin is found to be (much) younger than the
earth twin, as both twins expected. Explain.
Most explanations
of this problem that you see are either incomplete, saying the count of
light pulses (somehow) work out, or are based on time dilation (tricky),
or use 'world line' analysis. World line analysis is a powerful and general
tool for studying special relativity problems, but if you aren't familiar
with it (and I am not), it's not very explanatory.
Most newcomer
approach this problem by applying time dilation (moving clocks go slower),
and then realize that each twin thinks the other is moving and hence aging
more slowly, hence the paradox. In fact most solutions to the problem agree
that on the outbound leg this is exactly true, the paradox is alive
and well. This is a pretty tricky problem in special relativity. A good
way to approach this problem is to diagram out how the spaceship moves
and light flashes travel in space. From earth perspective this is not too
difficult, it's harder to do from the spaceship point of view.
My explanation of the twin paradox problem
Here's my
analysis of the twin paradox problem. I came up with this analyis on my
own, and despite a lot of research into the problem I have yet to see anything
like it. My analysis is based on length contraction, not time dilation.
I think this is a much more intuitive and easy to understand approach than
the usual one that explains the paradox in terms of time dilation.
The perception
of paradox, referred to as the twin paradox (sometimes called the 'clock
paradox') is caused by the error of assuming that relativity implies that
only relative motion between objects should be considered in determining
clock rates. The result of this error is the prediction that upon return
to Earth, each twin sees the other as younger -- which is clearly impossible.
(Wikipedia)
One twin travels in a spaceship to a star 32
light-years away (as seen by earth) at speed is 0.995c and returns immediately
at the same speed. The other twin stays on earth. They flash light beams
at each other once a second (local time). The Lorentz dilation/length contraction
factor for 0.995c is 1/sqrt (1 -.995^2) = 10. When the traveling twin returns
to earth he has aged 6.4 years, whereas the earth twin has aged 64 years.
Overview
--- Earth starts firing light flashes into space once a second when the
spaceship leaves. Relatively few (only 1 in 200) of the light flashes reach
the ship on the outbound leg since the ship is traveling almost as fast
as the light flashes. On the inbound leg the light flashes are all lined
up in a row (in space) as the ship heads into them. The key to my explanation
is to visualize how the light pulses exist in space from earth's point
of view, then to employ length contraction to show that the arrangement
in space of the light flashes looks the same to the twin in the ship except
squeezed together (length contracted) by a factor of 10. Finally the doppler
effect (as seen from the spaceship) must be factored in.
Inbound
leg --- When the ship turns around and starts back to earth most (99.5%)
of the light flashes have still not having reached the ship and are lined
up in a row in space separated in distance by 1 light second (as seen by
earth). However, the twin in the spaceship sees the world outside the spaceship
as length contracted by a factor of 10, so he sees the light flashes
are only separated in distance by 0.1 light second. Furthermore, since
he is traveling toward each light flash at almost the same speed as the
light flash is traveling toward him, the ship and the light meet (about)
halfway at a distance of 0.05 light second (as seen on the spaceship).
This is the doppler effect. The result is that on the inbound leg the spaceship
runs into another of the row of light flashes each 1/20 of a second. So
in the 3.2 years (as seen from the spaceship) it takes the space ship to
leave the star and return to earth, the ship counts (about) 20 x 3.2 yr
= 64 years worth of earth light pulses.
Outbound
leg --- The spaceship sees the light flashes behind the ship as separated
in distance by 0.1 light second, which is 1/10 of the distance separation
as seen from earth. Since the spaceship is only slower than the light by
a factor of 1/200, the time between light flashes reaching the space ship
is stretched out 200 times from 0.1 second to 20 seconds (as seen on the
spaceship). Therefore the ship counts (about) 1/20 x 3.2 yr = 2 months
worth of earth light flashes on the outbound leg.
Travel to a star 32 light years away
A excellent
relativity example is a spaceship traveling from earth to a star and back
at a constant speed with the spaceship flashing a beacon at a regular rate.
By thinking about the trip from the perspective of earthmen and spacemen
the time dilation/length contraction duality is illustrated. How the earthmen
see the flashing beacon is affected by time dilation and the doppler effect.
The sketch (below) shows how the doppler effect both stretches (outleg)
and contracts (in leg) the flash timing as seen by earthmen, allowing the
doppler effect to be disentangled from time dilation.
By having one
twin ride on the spaceship while the other twin remains on earth, it sets
the stage to explain the classic relativity twin paradox. At the
end of the trip one twin has aged less than the other. Why, and which one
is younger? The twin paradox is classic case where time dilation and length
contraction fail (or seem to fail).
The specifics
are these --- One twin gets on a spaceship and travels to a star 32 light
years away at (about) 86.6% speed of light, then immediately turns around
and comes back to earth at the same speed. A speed of 0.866 c gives us
a nice round number for relativistic time dilation & length contraction,
since sqrt{1-(v/c)^2} = 0.5. We will assume the time it takes the spaceship
to accelerate and decelerate is negligible, because there is no theoretical
limit on acceleration (unlike velocity!), all you need do is pour on the
power. The spaceship's position vs time (as seen from earth's perspective)
is a triangle, as shown in the sketch below.
Since the spaceship
is going reasonably close to the speed of light (0.866 c), from the earthmen's
perspective the total travel time to a star at 32 light years and back
is a just a little more than 64 light years, or 73.9 years (= 2 x 32 years/0.866).
To the spacemen zipping along relative to earth at 0.866 c, the distance
to the star looks to them to be contracted by a factor of two (=
1/sqrt{1-.866^2}) to 16 light years. So the spacemen see the total travel
time to a star at 16 light years and back is a just a little more than
32 light years, or 36.95 years ( = 2 x 16 years/0.866), and of course,
36.95 years is how much the spacemen expect to age during the journey.
Before the
trip starts, the twins agree that the both the spaceship and earth will
both fire a brief light flash every five years (local time). The earthmen
'know' (due to time dilation) that the spacemen are aging at only half
the rate of earthmen, so from earth's perspective the spaceship will flash
only every ten years, and that the doppler effect, since the spaceship
is at different distances from earth at each flash, will strongly affect
how the flashes are seen on earth. The sketch (below) shows the path
of all the light flashes (from earth's perspective). The pencil diagonals
(w/down arrows) are the light flashes fired from the spaceship and the
red diagonals (w/up arrows) are the light flashes fired from earth.
Summarizing, the parameters:
| Total trip
(out and back) |
Earthmen see |
Spacemen see |
| distance |
64 light years |
32 light years |
| speed |
0.866 c |
0.866 c |
Time dilation/Length contraction
sqrt{1-(v/c)^2} = sqrt{1-.866^2} |
0.5 |
0.5 |
| travel time |
73.9 years |
36.95 years |
Doppler effect (for ship flashes)
Out leg
In leg |
(1+.866c/c)=1.866
(1-.866c/c) =0.134 |
|
Doppler effect (for earth flashes)
Out leg
In leg |
1/(1-.866c/c) =7.46
1/(1+.866c/c)=0.536 |
|
speed of spaceship
relative to earth |
64 lyr/73.9 yr
= .866 c |
32 lyr/36.95 yr
= .866 c |
spaceship flash rate
(@ 5 yr local time)
(not including doppler effect) |
5 years x (1/0.5) =
10 years |
5 years |
spaceship flash rate
(@ 5 yr local time)
(including doppler effect)
Out leg
In leg |
10 years x 1.866 = 18.66
10 years x 0.134 = 1.34 |
5 years |
| # of spaceship flashes (sent/received) |
7 |
7 |
An important
point is this --- earthmen and spacemen always agree on what the
relative velocity is between them. They disagree on the travel time and
the travel distance, but they agree that the relative velocity between
the spaceship and the earth is either +0.866 c or -0.866 c. The reason,
of course, is that for the spaceman both distance and time are shortened
by the same (Lorentz) factor leaving velocity unchanged.
Check on doppler effect (for earth flashes)
On the out
leg the it takes a long time for the light flashes sent from earth to reach
the ship because the ship is racing away from earth at nearly the speed
of light. The out leg doppler effect (from earth perspecive) is easily
calculated: equate the distance of the ship from earth and the distance
of the first light flast (sent 5 years after the ship).
Distance of ship from earth = 0.866c x earth time
Distance of first light flash from earth = c x (earth time - 5 yr)
equate and solve for earth time
0.866c x earth time = c x (earth time - 5 yr)
earth time x (1 - 0.866) = 5 yr
earth time = 1/(1 - 0.866) x 5 yr
so
Doppler effect (out leg) = 1/(1 - 0.866)
= 7.46
The in leg
doppler calulation, where the ship is heading into the flashes from earth,
is sum the ship travel distance and flash travel distance to equal to the
5 light years distance between earth light flashes.
flash travel distance + ship travel distance = 5 light years
c x earth time +0.866c x earth time = 5 yr x c
(1 + 0.866) earth time = 5 yr
earth time = 1/(1+0.866) x 5 yr
so
Doppler effect (in leg) = 1/(1 + 0.866)
= 0.536
View of clock based light flashes from earth's perspective
Below is a
sketch I did showing how clock based light flashes (spaced 5 years local
time) sent from the space ship and sent from earth appear from earth's
perspective.
On the outbound
leg doppler causes the time between pulses to be stretched out and on the
inbound leg squeezed together, but notice the asymmetry. The spaceship
sees the earth flash rate (red) increase when the ship reverses direction
at the middle of its journey (at the star) and stay high all the way home,
but earth sees the spaceship flash rate (pencil) increase only near the
end of the journey. The spaceship counts 14 earth flashes, so the space
twin knows 70 years have passed on earth, whereas earth counts only 7 flashes,
so the earth twin knows only 35 years have passed on the spaceship.
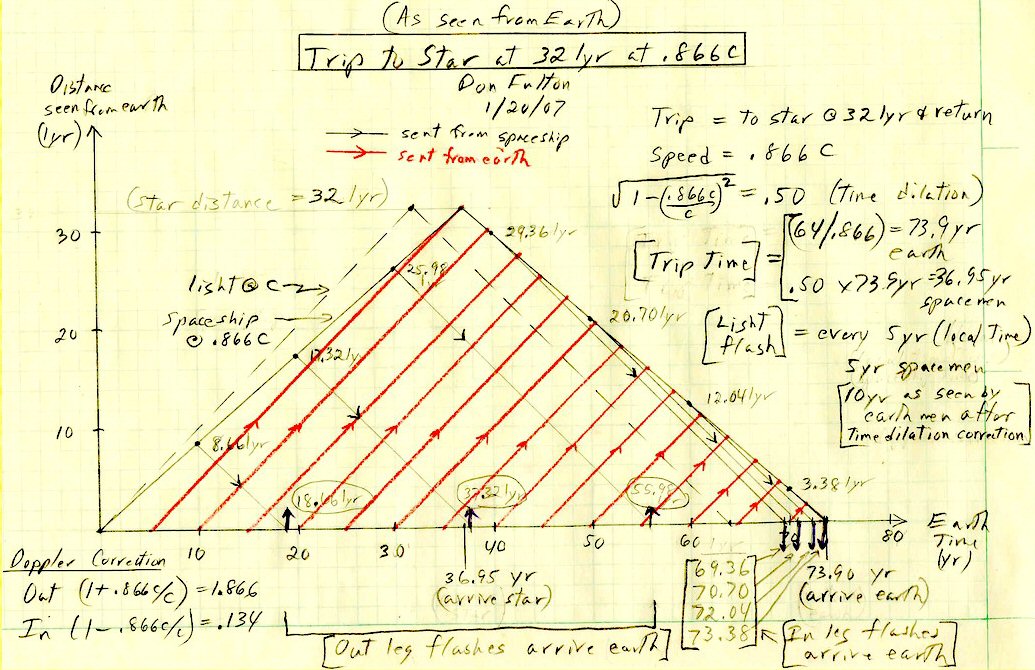
From the spacemen's
perspective they are sending a flash out every five years, for a total
number of flashes of seven on what they see as a 36.95 year (total) journey.
The earthmen 'know' (due to time dilation) that the spaceship clock is
running only only half as fast as the earth clock, so five years to a spaceman
is ten years to an earthman. Hence earthmen 'know' that (as measured by
earth time) the spaceship will flash every ten years for a total of seven
flashes in a 73.9 year (total) journey.
However, the
spaceship is at a different distance from earth each time it flashes, hence
the travel time of each light flash to earth is different. As can be seen
in the sketch above, the three flashes sent on the 'out leg' arrive on
earth separated by 18.66 years, whereas the four flashes sent on the 'in
leg' arrive on earth separated by only 1.34 years. On the 'out leg'
the spaceship and light are going in the opposite directions, so the doppler
multiplier is 1.866 = (1 + .866), stretching 10 years to 18.66 years. On
the 'in leg' the spaceship and light are going in the same direction
(spaceship traveling only a little slower than the light), so the doppler
multiplier is 0.134 = (1 - .866), shrinking 10 years to 1.34 years.
Twin paradox
When
the twins meet again on earth after the journey, how have they aged?
The official 'right' answer is that the twin who stayed on earth has aged
73.9 years, while the twin who traveled on the spaceship aged 1/2 this,
or 36.95 years.
Is this not
just a simple case of time dilation and length contraction? It seems
so. Does not the earth bound twin see the clocks on the fast moving spaceship
running slow, so of course he is not surprised that he finds his spaceship
twin has aged less? Also the time dilation equation has only v^2 in it,
so the earth twin see the spaceship's clocks running slow on both the outbound
and inbound legs of the journey, shouldn't he? Correspondingly the spaceship
twin see the universe whipping past, so for him the distance to the star
looks contracted. He sees the distance to the star as 16 light years, not
32 light years. Hence, he is not surprised that during the journey he has
aged only aged a little more than 32 years (36.95 years), because for him
this is how long the trip seemed to take.
Where is the paradox?
So where's the paradox?
Well, is not the spaceship twin perfectly free to consider that his spaceship
did not move and the earth was moving? He would see the earth zipping away
and back. Should not the spaceman then see earth bound clocks running slow
and see his earth bound twin aging more slowly than him? It seems so. Whoa,
there's a contradiction here! Both twins seem able to argue the other twin
was the one who moved, and hence the other twin aged more slowly! No wonder
it's called the twin paradox.
Many books
explain
(?)
the twin paradox by saying the situation of the twins is not the same.
They say the spaceship twin decelerated to zero and then back up to speed.
So what? Doesn't the spaceship twin see the earth do the same thing? And
all the lorentz equations have only the speed squared in them. What difference
does a speed reversal make? Well, it's more than the speed reversal
...
Above
we asked, "Is not the spaceship twin perfectly free to consider that his
spaceship did not move?" We implied the answer was yes, but if you think
about it, the answer is no. Four times during the journey the space twin
has sensed (& can measure) that his spaceship has accelerated or decelerated,
so the space twin knows he has moved. This is a key issue in understanding
the nature of time and space (see time and sapce below).
Is there is still
a puzzle here? Maybe. This is not a case of uniform motion,
yet time dilation and length contraction can be applied to get the right
answer. What I want to know is when can you apply time dilation/length
contraction, and when can't you? I have ordered a book by David Merimen,
who is reputed to be the best at explaining Special Relativity. We'll see
what he has to say. I know one way the twin paradox is explained is to
detailed it out. This can be done by having the space ship fire a light
flash at a regular rate based on the spaceship clock, and then figuring
out how those light flashes are seen on earth. Another step up in complexity
used to solve special relativity problems is to graph 'world lines', which
are space and time diagrams.
Update --- Is there is still a puzzle here? Well,
not really. Relativistic time dilation and length contraction multipliers
always
seem
to apply. Sometimes they alone will give the right answers, for example
to travel times and distances. But when an observer in one frame tries
to directly observe the clock or actions? (via light of course) in a moving
frame, the doppler effect comes into play and the doppler multiplier must
also
be used.
How is a moving flashing beacon seen?
The spaceship
trip to a star 32 light years away at 0.866 c and return can be understood
much better if we add light beacons, on earth and on the spaceship, that
flash at a regular rate controlled by the local clocks. In this way both
spacemen and earthmen can observe the other guys clock. Let's assume that
beacons flash when the local clocks click off five years, so earth is going
to flash 14 times during the journey and the spacemen, who see the journey
as only half as long, are going to flash their beacon 7 times.
Case 1 -- earthmen's view
The earthmen
'know' that the spacemen's clocks are running 2 times (= 1/sqrt{1-.866^2})
slower than earth clocks, so (from an earth perspective) the spacemen are
only going to flash every 10 years. So do the earthmen expect to see a
flash (arrive on earth) every 10 years? Answer is no! The reason, and here's
where it gets interesting, is that earthmen know the flashing spaceship
is moving, so the
doppler effect must also be considered.
The doppler
effect, which is usually associated with red and blue frequency shifts
in the absorption line in the spectrum of stars and galaxies, also affects
the time between light flashes. From earth's perspective the spaceship
will move in the 10 years between flashes emitted by the spaceship away
from the earth by 8.66 light years (0.866 x 10 light years). Therefore
the time as seen on earth between light flashes from the spaceship is the
time between light flashes (emitted from the spaceship) plus the extra
travel time to earth since the spaceship is further away. The general formula
for time between pulses as seen on earth is
local clock period x time dilation factor x (moving away)
doppler effect
5 year x (1/sqrt{1 - (v/c)^2}) x [1
+ v/c]
where
v = 0.866 c
5 year x 2 x [1 + 0.866] = 18.66 years
Note on the outward leg of the journey the emitted time
between pulses (10 years) is seen on earth to be nearly doubled
(18.66 years) because the doppler effect, which is the moving away of the
spaceship between pulses.
On the outward
leg the spacemen send 3 flashes during what they see as a 18.475 year trip
to the star. The combined effect of time dilation (affecting the emitting
rate) and doppler (affecting how the time between pulses is seen) causes
the time elapsed on earth to receive these three pulses to be almost 56
years! On the return leg the doppler effect works to reduce the time between
pulses. And when the spaceship is traveling fairly close to the speed of
light and in the same direction of the light it emits, it nearly nearly
keeps up with its light flashes. The formula has the same time dilation
term, but the sign of v in the doppler term is reversed (v = -0.866 c).
5 year x 2 x [1 + (-0.866c/c)] = 10 years (1 -
0.866)
= 10 years (0.134)
= 1.34 years
Notice the
huge effect the sign reversal makes. Whereas it took almost 56 years on
earth to receive the three pulses sent on the outbound leg, the four pulses
sent on the inbound leg arrive squished together, all four pulses arriving
in (about) four years just slightly ahead of the spaceship arriving on
earth. Notice also that on the inbound leg to the earthmen, who are looking
at the spaceship clock via the flashes, if they forget to take the doppler
effect into account, will incorrectly assume that the spaceship
clock does not 'look' slowed down, i.e. that the spaceship time is not
dilated.
The dopper
effect is a first order effect that is sign dependent, going as [1 +/-(
v/c)], whereas the relativistic time dilation effect is second order effect
that is not sign dependent going as 1/sqrt{1-(v/c)^2}. The general
rule for an observed clock is
When
the source is coming toward the the observer, the (apparent) speeding up
of the moving clock due to the dopper effect (seen as a crowding of pulses)
is always stronger than the (real) slowing down of the clock due
to relativistic time dilation (seen as a spreading out of pulses).
How is it spacemen measure c for the speed of light?
An interesting
question not often addressed (and which can be very confusing) is this
--- Can earthmen explain how it is that when spacemen measure the
speed of light (in their moving spaceship lab) they get the same value
as earthmen. And, of course, they better get the same value because this
is a key principle of relativity?
Let's extend
our spaceship example --- Before the journey started the spacemen and earthmen
set up similar light speed measuring apartus in their labs and get the
same results. Using a ruler they measured out 100 ft and with a (local)
clock that has 1 count/nsec they time how long it takes a light pulse to
cross the measured distance. In the spaceship the measured course is laid
out so tha the light travels in the same direction that the spaceship is
traveling. On earth before the journey started both labs find it takes
100 counts of the clock for light to travel the 100 ft course, which is
a speed of 1nsec/foot (eq to 3 x 10^8 m/sec).
During the
journey when the spaceship is traveling (with respect to earth) at 0.866
c the spacemen repeat the experiment and get the same result: 100 counts.
Of course, to the spacemen this is not surprising, since to them their
spacelab looks exactly like it did on earth. When they check the
measured distance with their ruler it still measures 100 ft, and as far
as they can tell their (local) clock is running just like it did on earth.
How do the
earthmen 'explain' why the spacemen in their spacelab, moving at 0.866
c with respect to earth, still measure the same speed of light (100 counts).
From the earthmen's point of view the moving spacelab is not the same as
it was on earth. One, due to lenght contraction, the spaceship has squashed
front to back, so the measured course is really only 50 feet, not 100 feet
as it was originally. Two, due to time dilation, the spaceship clock has
slowed down (relative to its speed on earth) such that it is running only
half as fast. In the time it takes the spaceship clock to count 100 beats
the earth clock makes 200 beats.
Since velocity
is delta distance divided by delta time, earthmen observing (in their
mind's eye) the experiment on the moving spaceship say the distance is
down by two and the time is up by two, so the speed is different by four!!
Yikes, I always get this result. Where is the error here??
Einstein in his 20's
In 1902 Henri
Poincare (who is known to all math students) wrote a book listing three
big unsolved problems in physics:
photoelectric effect, brownian
motion, and luminiferous ether. Einstein read the book in 1904
(at age 24) and within one year solved all three problems. Einstein, who
had failed to get his doctorate, solved the problems working alone while
employed full time in an (engineering) job and supporting a wife and child..
At age 25 he had four papers published in a leading German physics journal
(in March, April, May and June of 1905). These four papers, each now a
classic, solved all three problems laid out by Poincare. (Ref:
Einstein 1905: The Standard of Greatness, by John S. Rigden)
1) The brownian
motion problem was that small pollen grains suspended in water could be
seen under a microscope to constantly zig zag around. No one had any explanation
for this motion. At the time little to nothing was known about atoms, how
big were they, or even if they existed.
Einstein's
brownian motion paper showed how atoms were responsible for the jiggly
motion and showed how this motion could be used to calculate the (approximate)
size of atoms. He won a Noble prize for his work on brownian motion.
2) The photoelectric
problem was that high frequency ultraviolet light was known to eject electrons
from a metal plate, but lower frequency (visible) light did not do this
regardless of how bright the source was. This could not be explained by
then current wave theory of light.
Einstein's
photoelectric paper showed that the experimental result could be explained
if light was quantified (now called a photon) and that the energy in each
quantum of light was proportional to the frequency of the light.
This later became one of the core concepts in the development (by others)
of quantum physics.
3) At the time
all known waves were vibrations of some substance (sound is a vibration
of air or water). When evidence piled up that light was a wave (it refracted
and reflected), it was generally accepted that there must exist an as yet
undetected substance (known as 'the ether') that was everywhere (including
in space) and that light was a vibration of the ether. The ether also nicely
explained why the speed of light was independent of the speed of the source
of the light. If it was assumed that the ether was fixed (unmoving) and
that planets and stars moved through it, then of course, light moved at
a speed relative to the fixed ether, not the source.
One difficulty
with the ether was no one could come up with a reasonable model for the
ether (people mostly built mechanical models with springs and weights in
those days). The properties of the ether were very hard to explain, because
on the one hand the ether needed to be very stiff to support the very frequencies
and high speed of light, yet on the other hand it had to be incredible
thin and tenuous so that planets and binary stars could move easily through
it. By the mid 1880's an even more serious problem with the ether arose.
A series of experiments was done to measure the slight variations in the
speed of light expected as the earth traveled through the ether around
the sun (famous Michelson-Morley experiments), but they found the speed
of light was always the same regardless of orientation of the apparatus
or the season.
Einstein's
ether paper (completely) detailed his new theory of special relativity.
It showed that if the speed of light was accepted as a constant (consistent
with experiments), then the concept of time as absolute (proposed by Newton
and almost universally accepted) must be wrong. It showed how time and
length must vary when seen by moving observers, and the theory predicted
that the variations in time and space were exactly what Lorentz had earlier
proposed (ad hoc) to explain away the experiments that had failed to find
a variation in the speed of light. The theory proposed an entirely new
and revolutionary view of space and time in which the the speed of light
measured by all (inertial) observers would be the same without need for
an ether. In other words, there was no ether.
In Sept of
the same year (1905) Einstein published a three page supplement to the
relativity paper that derived one of the most famous equations in physics
(E= mc^2). This equation showed that mass carried a fixed and very large
amount of energy and was (in some sense) equivalent to energy. (Ohanian
in his book Einstein's Mistakes says Einstein proof is not general that
it is restricted to low speeds, but it was proved in general by others
a few years later.)
To the non-scientist
it was sometime stated as, mass is frozen energy. Ohanian calls
mass congealed energy and contrasts it with ordinary energy that
is free to move around and be transformed. He makes an analogy with water/ice.
Ice in ice sheets on earth is congrealed water, whereas water in
the oceans is free to move around.
Nature of time and space
(from the book Life of the Cosmos by Less Smolin)
Galileo and
Newton both well understood that you cannot determine if you are
at rest or moving at a constant speed, but you can determine, without
reference to anything external, if you are rotating or accelerating.
Smolin says of this, "the distinction between uniform motion and accelerating
motion is absolutely central to our understanding of motion" and
that this is a "fundamental discovery, and the deepest mystery, in the
whole history of physical science" (p 230)
Newton formulated
his
laws of motion by explicitly assuming that space and time were absolutely
fixed. Many, like Leibniz, thought this was crazy, that you could only
determine if you were moving by making reference to other parts of the
universe, that you needed to construct equations of motion using relative
motion.. But Newton, no dummy he, saw that absolute space and time, even
if philosophically flawed, was a good starting point for formulating equations
of motions because the equations were greatly simplified. Example, equations
like (Force = mass x acceleration) couldn't be much simpler.
In the 19th
century the concepts of an observer & frame of reference
were invented. This allowed Newton's equations of motion to be used without
reference to absolute space and time. You could use Newton's equation and
say you were moving with respect to a frame of reference. Frames of reference
that were fixed or moving at constant speeds to each other became a special
case and were called inertial frames. In these frames an observer
is unable to determine if his frame is moving or not, so he is allowed
to assume it is at rest and that other inertial frames are moving.
A puzzling
think about Maxwell's equations (formulated 1860's) was that they gave
the speed of light without reference to any frame. Forty years later
Einstein took this as a starting point and developed special relativity
as an explanation of this puzzle.
Einstein's
special relativity applies only to inertial frames and is concerned
with how observers in one inertial frame, which they can assume is at rest,
see motion in another inertial frame, which they assert is moving.
Smolin continues
-- "The relativity of motion is both a fact and a mystery." He says the
key question to ask to penetrate the mystery is "What is the cause of the
distinction between velocity (which you cannot feel) and acceleration (which
you can feel)." (p 230) Ernest Mach had a (possible) answer.
Is Special Relativity hard to understand?
There is no
question (in my mind) that getting a really good understanding of special
relativity is difficult. Consider the following:
History --- A. P. French in his book on relativity
says that in in 1957-1959 the Twin Pradox was "raging controversy" in physics.
And he adds that in a book of (paper) reprints on special relativity in
1963 by the American Institue of Physics 9 of the 17 papers reprinted were
devoted to the twin paradox problem. Note this is (about) 50 years
after the twin paradox/clock problem was first mentioned by Einstein!!
A classic example
of the difficulty of special relativity is Herbert Dingle (1890 – 1978).
He was an English astronomer, President of the Royal Astronomical
Society, and in 1922 authored a book on relativity. Yet in his later years
he became convinced that special relativity was wrong and wrote a book
about it. He was not nuts, he just (according to others) got tripped up
on some subtlies of special relativity. More details can be found
searching Dingle and Wikipedia.
* Simpler relativity
problems generally involve just two object. Problems with three moving
objects are a lot trickier.
* There is
the conceptual difficulty of keeping straight the difference between what
you 'see' from what you 'know' when looking at a moving object. When you
look at a moving clock, you are seeing a real effect (time dilation) through
the distorting (lens) of the doppler effect. Some reference talk in terms
of how the moving clock appears (including the doppler effect), while others
separate out the doppler effect to talk about how the moving clock is (really)
slowed, even if it may appear to be running fast. And to add to the confusion
the doppler distortion equation comes in four flavors, depending on whose
viewpoint is taken and whether relative motion is moving away or together:
(1-v/c), (1+v/c), 1/(1-v/c), 1/(1+v/c).
* Combo equation
--- You think you have the doppler effect all figured out, and then you
come upon a reference that uses the relativistic doppler effect.
What the hell is that? It turns out this is a combo equation. Instead
of an analysis using (time dilation x doppler), relativistic doppler combines
the time dilation equation and the Doppler equation into a new (combo)
equation. For example:
doppler x time dilation
= relativistic doppler
1/(1 - v/c) x sqrt {1 - ( v/c)^2} = sqrt{(1 + v/c)/(1
- v/c)}
Check
sqrt {1 - ( v/c)^2} = (1 -v/c) x sqrt{(1 + v/c)/(1 - v/c)}
= sqrt{[(1 + v/c)/(1 - v/c)] x (1 - v/c)^2}
= sqrt{[(1 + v/c) x (1 - v/c)}
= sqrt{1 +v/c -v/c -(v/c)^2}
= sqrt{1 - (v/c)^2}
* There is
a four dimension (three space + time) formalism, called world line analysis,
that apparently allows many relativity problems to be graphed. While
I have not studied it, getting the right answer this way may (or may not)
help you to better understand relativity.
Paradoxes --- When you read the
explanation of various paradoxes, you find the analysis given is almost
always different in different references. If special relativity is so simple,
why is that?
Some of the
more tricky and/or more difficult to solve problems in special relativity
have become famous. Some of the famous problems or paradoxes go back
to the early days of relativity, like the Twin Paradox problem,
but others are relatively new, like the Bell's spaceship paradox (1976).
Wikipedia has a list of these problems and paradoxes.
Furthermore
some of the published, standard, explanations of paradoxes are very hard
to swallow. For example, the analysis of the twin paradox in the recent
book E=Einstein has the spacemen seeing the clock on earth as running slower
than the spaceship clock on both the outbound and inbound legs.
Yet the spaceship twin is going to arrive home younger. What?? The hard
to swallow part is that during the brief interval at the star while the
spaceship decelerates and accelerates again the spaceship twin sees virtually
all the aging of the earth bound twin happening during this brief time!
(See my own much more common sense explanation of the twin paradox based
on length contraction).
If we lived
at a time when astronauts, where going to stars at near the speed of light,
I think it would be different. It would then be common knowledge that the
astronauts would sense the journey time and distance very differently from
those on earth.
Why is the universe not rotating?
Almost every
body we see in the universe has angular momentum and rotates. The earth
rotates on its axis as does the sun, every planet, stars and black holes.
The earth, planets, and every object in the solar system rotates around
the sun. The solar system is embedded in an arm of a spiral galaxy and
is rotating around the center of the galaxy. There's even a mechanism whereby
objects like neutrons stars and black holes can be 'spun up' when rotating
gas falls on them.
But... the
universe as a whole with respect to us does not appear to be rotating.
Weird... As Smolin points out there is nothing in Newtonian mechanics that
says it can't, and Einstein's general relativity doesn't prevent it either.
In fact in 1949 Godel (famous mathematician) found a rotating, static,
universe was a solution to Einstein's general fields equation, the outward
force of rotation counteracting the inward force of gravity. Godel argued
that in such a universe you would know it was the universe rotating and
not you if you did not feel dizzy! From a Newtonian perspective
of absolute time and space it must just be coincidence that the universe
is not rotating. (p 231)
Mach in the
1880's argued that when you sense rotation, it must be because you rotating
with respect to something and that something is the universe. Seems pretty
mushy to me, and it's not proven, but as Smolin points out this view point
does provide a (sort of) explanation as to why the universe we see around
us is not rotating.
Aside --- How can the rotation of the universe
be measured? Note you cannot use galaxy red and blue shift doppler effects.
Doppler only measures the component of velocity on the line of sight
between the object and earth. Rotation (relative to earth) would be at
90 degrees to our line of sight, and thus would cause no doppler effect.
A goggle search
shows two methods. One is based on using measured planet positions (with
respect to the background stars) in a Kepler/Newton planet rotation model.
This model has a lot of correction factors, one of which is the rotation
of the background stars. Within experimental error this term is zero. (my
comment --- Does this make any sense? All the background stars are in our
own galaxy. This method would only makes sense if planet positions are
measured with respect to the background galaxies, which I bet is impossible.)
The second method is based on analysis of the background microwave background.
The argument seems to be 'If the universe were rotating, the rotational
axis would single out a preferred direction in space', and there is no
evidence of this.
Nature of simultaneous
Simple version
Light bulb
flashes in the center of a moving train car. People in the train car know
(& can measure) the speed of light is the same in every direction,
so since the light bulb is in the center of the car, they see the light
hit the front and back of the car simultaneously.
The people
on the platform see that as the light is traveling the car moves forward
a little, so they see that the light has less distance to travel to reach
the back of the car and more distance to hit the front of the car. It's
an experimental fact that the speed of light is not affected by the speed
of its source, so unlike say a ball thrown in the car, the speed of light
from the bulb is not given any push forward by the speed of the bulb. Therefore
the people on the platform see the two events (i.e. light hitting the car
ends) as not simultaneously.
Fancy version -- (frin Brian Greene's book,
The
Elegant Universe)
Two
warring kings sit at opposite ends of a long table ready to sign a peace
agreement, but neither wants to sign before the other. To solve the problem
a light bulb, not lit, is placed in the exact center of the table. The
kings agree that they will each sign the instant they see the light bulb
come on. The know it takes a finite time for the light (at 1 nsec/ft) to
travel from the bulb to the end of the table, but since they are each the
same number of feet from the bulb, they know they will be signing simultaneously.
I forgot
to tell you the table and signing ceremony is in a train car moving at
a constant speed. Does it make any difference to the kings? Answer, no.
As Galileo argued nearly 400 years ago, there is no test you can do to
determine if you are at rest or moving at a constant speed. Everything
will look exactly the same in the car to the kings whether the train
is at rest or moving (through the station) at a constant speed.
But
to the kings subjects looking on from the station there is a problem. They
don't see the signing as simultaneous. They see the king nearer the back
end of the train signing first, then later the king nearer the front end
signing. Why is this?
During the
time the light is traveling from the light bulb toward both ends of the
table the train is moving forward. The light does not get any special 'push'
forward from the speed of the train. One of the principles of relativity
is that the speed of light everyone sees (measures) is totally unaffected
by the speed of the body emitting the light. The kings' subjects on the
platform see the light heading toward the back of the train has less
distance
to travel, because while the light is traveling back the end of the table
moves forward a little. Similarly the light heading toward the front of
the train has more distance to travel, because while the light is
traveling forward the end of the table moves forward a little. Since the
light is traveling in both directions at c, it reaches the back end of
the table first because the distance it has to travel is less.
Moral of the
story --- An event (signing) seen as simultaneous to one group (those
in the moving train) is seen as not simultaneous to another group
(those outside the train). In general observers moving relative to each
other at constant speed will not agree on whether an event is simultaneous.
This is a fundamental result with great consequences about the nature of
time and space.
--------------------------------------------
Magnetic fields are 'caused' by relativity!
You often
see this claim --- Relativistic effects are only significant at
high speeds. Wrong, wrong!! Whoever says this doesn't understand
special relativity. In the same sense that the curvature of space (general
relativity) explains what gravity is, the motion of charges (special relativity)
explains what magnetism is.
In electrical
engineering electric and magnetic fields are treated as fundamental entities.
Both types of these fields exert forces on charged particles and store
energy in the fields. Electric fields are created by charges and
are measured in volts/distance. Magnetic fields are created by currents
and are measured in amps/distance. In a capacitor energy is stored in the
electric field. In an inductor energy is stored in the magnetic field.
Maxwell's equations describe how electric and magnetic fields are related
to charges and currents. Physicists take a different view. Physicists regard
the magnetic field as secondary to the electric field. The magnetic field
can be derived from the electric field with the magnetic field amplitude
(always) coming out to be electric field amplitude divided by the speed
of light squared.
Magnetic force vs electric force
Two electrons spaced at distance r feel an electric force outward (pushing
them apart).
Felec = 1/(4 pi e0) x q^2/r^2
where
e0 = permittivity of free space
If the same
two electrons at distance (r) apart are moving sideways to me with velocity
(v), they look to me like little currents (current is just moving charge),
so they make a magnetic field. I can calculate the magnetic field (B) from
the Biot-Savart law which physicist use to calculate the magnetic fields
from a small length (dl) of current (i) of length (dl).. Current is just
moving charge, so i=q/dt and idl = qdl/dt = qv. .
B = (u0/4 pi) x (idl)/r^2 = (u0/4 pi) x (qv)/r^2
where
u0 = permeability of free space
From the general (vector) force equation (F = q
(E + v cross B) magnetic force in this case is qvB and its direction to
inward. (An electrical engineer can figure the direction from the right
hand rule of currents and remembering that the charge of q is negative.)
Fmag = qv x B
Fmag = (u0/4 pi) x (qv)^2/r^2
But there is a relation ship between e0, u0 and the speed
of light (c)
c= 1/(sq rt {e0 u0)
c^2 = 1/(e0 u0)
u0 = 1/(e0 c^2)
eliminating u0 from Fmag we get
Fmag = (u0/4 pi) x (qv)^2/r^2
= (1/e0 c^2)/(4 pi) x (qv)^2/r^2
= 1/(4 pi e0 c^2) x (qv)^2/r^2
= 1/(4 pi e0) x q^2/r^2 x (v/c)^2
but the first expression is just Felect, so we have
Fmag = Felect x (v/c)^2
Thus the net force (Fnet), which is the repulsive force
between two electrons moving at speed (v) relative to an observer, is the
large electric repulsive force (Felect) minus the normally much smaller
magnetic attractive force (Fmag).
Fnet = Felect - Fmag
Fnet = Felect x {1-(v/c)^2}
As you can
see above 'motion fudge factor' reducing the electric force {1-(v/c)^2}
between electrons turns out to be just the square of the relativistic 'fudge
factor' that appears in the special relativity length contraction. The
inward magnetic force between the electrons only equals the outward electric
force when the speed of the electrons (with respect to me) reaches the
speed of light. So magnetic force, which arrises when charges move, sure
looks like it's just a relativistic correction of electric force. And so
it is. This point of view provides us with an explantion of the origin
of the magnetic field and magnetic force.
There's a lot
of good stuff about special relativity at this link (Australian university)
http://www.phys.unsw.edu.au/einsteinlight/jw/module2_FEB.htm
Wikipedia comments on electromagnetism and relativity
this way:
"In
particular, a phenomenon that appears purely electric to one observer may
be purely magnetic to another, or more generally the relative contributions
of electricity and magnetism are dependent on the frame of reference. Thus,
special relativity "mixes" electricity and magnetism into a single, inseparable
phenomenon called electromagnetism (analogously to how special relativity
"mixes" space and time into spacetime). .. When both electricity and magnetism
are taken into account, the resulting theory (electromagnetism) is fully
consistent with special relativity." (Wikipedia, 'Magnetism')
Magnetic force between two parallel wires
A textbook
example for measuring magnetic force (as a function of current) is the
case of two parallel wires carrying the same current in the same direction.
There is an attractive force between the two wires. Normally in the textbooks
the force inward is derived from the electromagnetic equations that relate
force, current and distance.
If we look
deep at two current carrying wires parallel wires, where at the currents
are equal and in the same direction, what we see is this. Two rows of negative
charge (free electrons in the metal wire) that are moving in parallel with
the same (average) velocity and two rows of positive charge (the atoms
of the metal wire that have lost an electron, called ions) that are not
moving. Above we derived the force between moving electrons as a static
electric repulsive force minus a velocity sensitive attractive magnetic
force.
Fnet = Felect - Fmag
Fmag = 1/(4 pi e0) x q^2/r^2 x (v/c)^2
There is a
positive ion in each wire for each negative electron, so in the case of
two parallel wires there is no static electric force between the wires
(Felect = 0). The remaining force between the wires is the attractive,
relativistic, magnetic force (Fmag), which varies as flow of charge (q
x v) squared, or current squared.
Magnetic field as seen by a test charge outside a wire
It is an amazing
thing is that magnetic forces and fields are (at root) really just relativistic
corrections of the electric field caused by the motion of electrons
that make up a current. In the case of forces on a test charge outside
a wire carrying a current the relativist nature of the magnetic field is
a more obvious. The text below shows that the magnetic force on a test
charge outside a wire is explained by invoking length contractionthat
slightly unbalances the normally exquisitely balanced positive and negative
forces of the electrons and copper ions in the wire.
But the really
incredible thing is that the speed of electrons in a wire (at a few amps),
which is the cause of this relativistic effect, is less than 1 mm/sec!!
This means, of course, that the resultant length contraction is unbelievably
tiny, about one part in 10^23, since (v/c)^2 = (10^-3/3 x 10^8)^2.
What this tells us is that electric forces from bare (unshielded) charges
must be astoundingly huge.
Current in
a copper wire is nothing more than a flow of loosely bound outer electrons
of the copper atoms moving along with wire. The wire as a whole is electrically
neutral. The freely moving negatively charged electrons are balanced by
the non-moving positively charged atoms (ions) that have lost an electron
to the current. A (test) electron near, but outside, a wire carrying a
current feels no force if the test electron is not moving (because
the wire is neutral). But if the outside test electron is moving (either
as a free electron or as part of a current in another wire), it does feel
a force. The force felt by the moving test electron is usually described
as coming from the magnetic field created by the current in the wire {Force
= q(v cross B)}
If viewed at
the charge level, however, thing look different. Let's assume the outside
freely moving test electron is moving parallel to the moving electrons
in the wire and at the same (average) speed. When the wire is viewed from
(a frame attached to) the outside moving electron, the electrons in the
wire are seen to be fixed and the positively charged ions moving backwards.
Even though speeds are slow relativity arguments can be applied, and the
spacing between the positively charged ions, as seen from the freely moving
test electron, is length contracted. The key is this: the
outside test electron sees the positively charged ions more closely
packed than the negatively charged moving electrons of the wire, so
from the point of view of the outside moving test electron the wire has
a net positive charge. Since opposite charges attact, the
outside test electron feels a force pulling it toward the wire.
The (average)
speed of moving electrons is a wire is very slow (< 1mm/sec), so on
the one hand the relativistic length contraction is unbelievably tiny,
but on the other hand the attractive/repulsive forces between bare charges
is incredibly huge. One references summarized this example this way:
This
is why there are magnetic fields: their effects are a manifestation of
the fact that charges exert electrostatic forces on other charges, and
that special relativity makes current-carrying wires which are neutral
in one frame appear charged in another frame.
http://web.hep.uiuc.edu/home/g-gollin/relativity/p112_relativity_14.html
--------------------------------------------
How time dilation and length contraction allow everyone
to measure the same speed
We can now
explain how earthmen and moving spacement both get the same result when
measuring the speed of light, or any speed. The key is that speed is a
ratio
(distance/time).
A spaceman can (from our point of view) measure distance wrong and
measure time wrong, but still calculate (measure) correct speeds because
the distance and time errors cancel each other. Of course, the formula
for time dilation and length contraction have been constructed so that
they will divide out when the ratio of speed is calculated.
Consider, a
spaceman uses his clock to count how many beats it takes a photon to travel
across a test distance he has measured with his ruler.
Spaceman sees
--- Measures out a 1 foot test distance and counts 1,000 beats of his (local)
10^12 hz oscillator (period = 1 picosecend) clock. So spaceman calculates
speed of light = 1 foot/1 nsec or 3 x 10^8 m/sec.
Earthman sees
(assume v/c = 0.866, so sq rt (1-(v/c)^2) = 0.5) ---
1) Travel distance is only 6 inches, because the ruler the spaceman used
was contracted by a factor of 2. Since his distance is low, his calculated
speed due to this 'error' (alone) will be low by a factor of 2,
or in general by the length contraction factor {sq rt (1-(v/c)^2)}.
2) Time dilation causes everything on the spaceship (except photons) to
move slowly. So Earthmen see the oscillator running at half freq (period
= 2 nsec). We agree with spacement there were 1,000 beats during the photon
travel distance, earthmen measure the travel time at 1,000 x 2 nsec = 2
nsec. Yikes!!!
Earthmen say
moving 6 inches took 2 nsec or 1/4 ft/nsec . Where the hell is the error
here!!
figuring from the muon case
earthmen see
muons travel down 6,000 ft mountain in 6 usec. Speed close to c To explain
the observed high survival the time is assumed to be running slow on
the muon, such that the travel time was only 0.7 usec
muon men see
mountain only 700 t high so it can be traversed in 0.7 usec. Speed close
to c. Result only 30% decay.
|
earthmen see |
muon men see |
| travel time down mountain |
6 usec |
0.7 usec |
| mountain height |
6,000 ft |
700 ft |
| relative earth/muon speed |
6000 ft/6 usec =
1000 ft/usec
(close to c) |
700 ft/0.7 usec =
1000 ft/usec
(close to c) |
|
|
|
| time for photon travel the distance |
2 nsec (1000 beats of period 2 psec osc) |
1 nsec (1000 beats of period 2 psec osc) |
| distance |
2 feet/6 in
Yikes!! |
1 foot |
| measured speed of light |
2 ft/2nsec=1 ft/nsec |
1 ft/nsec |
-------------------------------
Mea speed across the shorten distance quickly. His speed
is scaled up by the factor {1/, the inverse of the contraction of his ruler.
Mistake
#2 is that his measured time (from our point of view) is too short because
his clock is beating too slow. Mistake #2 causes him to get a speed result
which is also too high, since he finds it takes a short time
for the photon to cross the measured distance. Yikes, I don't understand
this!!
Earthman sees
(looking at spaceman zooming by at 90% of speed of light ) --- Spaceman
has measured out 5.24 inch test distance and counts 437 beats of the clock.
Why???
(while we agree he counted 1,000 counts of his clock,
his clock is running slow so that each beat takes 2 picoseconds. So his
measured speed is 0.5 foot/2 nsec. Same problem!!)
--------------------------
Spacemen and
earthmen both agree --- clock on spaceship beats 1,000 times as photon
crosses measured distance.
Spacemen say
--- Measured distance was 1 ft and since 1,000 beats of the (local) 10^12
hz oscillator (period = 1 picosecend) clock means travel time was 1 nsec.
So spaceman measure speed of light = 1 foot/1 nsec.
Earthmen say
--- Distance was really 2.29 ft (length expansion???) and 1,000 beats of
the slowed down 10^12 hz oscillator (period = 1 picosecend) clock means
travel time was 2.29 nsec. So earthmen measure speed of light = 2.29 foot/2.29
nsec
----------------------------------
How time dilation and length contraction allow everyone
to measure the same speed (2nd try) (11/15/11)
Principle ---
Length contraction is (only) in the direction of travel
Everyone measures the same speed for light
From earth
we watch spacemen (in a glass space ship) going by as they measure the
speed of light.
* Inside the ship they orient a 1 ft ruler from front to back of the ship.
Inside they measure the travel time
of light along the ruler with their clock and get 1 nsec. (Visualize we
can watch the space ship clock move
and we see it hits the 1 nsec mark as the light photon crosses the end
of the ruler.)
-- Hence even though we measure the ruler as contracted and the travel
time along the ruler as extended
we can 'understand' how the spacemen get 1 nsec/ft because we can see their
clock hit 1 nsec when
the light crosses the end of their marked 1 ft ruler. In other words we
observe the simultaneous event of
the light photon crossing the end of the ruler and the marking on their
clock. We see the same spaceship
instrument readings as the spacemen.
* From earth perspective we see events happening more slowly on the ship,
so when we time the light travel
along the ruler using our earth clock we get more than 1 nsec, say
1.1 nsec. Thus the time dilation effect,
considered alone, would cause us to say that the speed of light
measured on this moving platform
would give a speed that is too low.
* Now we come to the crux of the matter. Does, or does not, length contraction
cancel out time dilation?
-- We see the ruler (oriented along the length of travel) as contracted,
so we measure it at less
than one foot, say 0.9 ft. So measuring with our instruments it takes 1.1
nsec for light to travel 0.9 ft.
Twice the error!
Does this violate
the principle, 'Everyone measures the same speed for light'? Maybe not.
My little though experiment says that if we try to measure the speed of
light with instruments in our frame as we observe the experiment
in a moving frame, the relativistic effects do not cancel
they add (really multiply). Also even if by some logic (with shrunk rulers),
we do argue there is calculation, when the ruler is turned 90 degrees the
cancellation will be gone, because time dilation will remain, whereas there
is no contraction in direction perpendicular to the direction of motion.
I bet the explanation
is that there is a corollary:
'Instruments must be in the same frame as the experimental apparatus'
While I can't find this explicitly stated in a search,
I suspect it is common sence. When it is stated an observer makes a measurment
in his reference frame, it is implied that the instruments he uses
are in his frame too.
Riff on '1/2' in energy formulas
Energy can
be stored in a lot of ways and a surprising number of the energy formulas
look very similar. The table below shows four of many. A moving mass stores
energy in motion, a compressed spring stores energy in material elastic
deformation, a capacitor with a voltage stores energy in an electric field,
an inductor with current stores energy in a magnetic field.
| Energy formula |
Parameters |
Energy stored |
| 1/2 m v^2 |
kinetic |
mass,
speed |
motion |
| 1/2 k x^2 |
linear
spring |
spring constant,
spring displacement |
material
elastic
deformation |
| 1/2 C V^2 |
capacitor |
capacitance,
voltage |
electric field |
| 1/2 L I^2 |
inductor |
inductance,
current |
magnetic field |
How come
all these formula have a '1/2'? Well let's start with zero energy
in a system and then pulse the power (off, on, off) to add some
energy. In mechanics power is the product of force x velocity, in electronics
power is current x voltage. In the following examples one power term is
held constant and the other power term ramps up linearly:
-- When you drop a body in the earth's gravitational
field, the force is (nominally) constant and the velocity ramps up linearly.
-- When you compress a (linear) spring by squeezing it
at a steady rate, the force ramps up linearly.
-- When you add charge to a capacitor with a constant
current source, the voltage on the capacitor ramps up linearly.
-- When you apply a constant voltage source across an
inductor, the current ramps up linearly.
Energy is the
integral of power, so the area under the power pulse is energy added to
the system. All these power pulses, being the product of a constant and
a ramp that starts at zero and then steps back to zero, have the shape
of a triangle. The area of a triangle is 1/2 times the peak
power times the time of the ramp. This is where the 1/2 comes from!
Here's it is
from another point of view. Consider the body dropped in earth's gravitational
field, which we assume constant. Since (E = force x distance), the kinetic
energy a falling body just depends on how far it has fallen. The energy
increases linearly with distance, and there is no '1/2' in the energy
equation if written in terms of force and distance. Of course, as a function
of time a falling body falls faster and faster, resulting in the distance
it has moved going up as the square of time. The math is this: velocity
increases linearly over time in a (constant) gravitation field, so speed
plotted vs time is a triangle. In time t the speed is at, where
a is the gravitational acceleration constant on earth (32ft/sec^2). The
distance moved is the area under the velocity triangle. The triangle shape
explains the '1/2' and since both the hor and vertical size of the triangle
grow with time, this explains why the distance increases as time squared.
(distance = 1/2 a t^2).
From still
another point of view --- The distance that a dropped body moves in a given
time is its average speed x time. Since the speed increases linearly
(from zero), its average speed (during the fall) must be equal to
1/2 of its present speed. There's the '1/2' again.
The point of
all this is that the '1/2' in the energy formula is related to the fact
that (if power is finite) it takes time to move energy in or out
of bodies. The flow of energy in/out over time is why there is a 1/2 in
all the above square law energy formulas.
Why no '1/2' in Einstein's formula?
Curiously,
Einstein's famous formula E= m c^2 is similar to the energy formulas above
except
it's missing the '1/2'. In all the other energy formulas the 1/2
arises during the process when the energy is added to the system. Einstein's
formula is interpreted as the rest energy of mass. There is no charging
process, the energy is always there. I think that's why there is no '1/2'
in Einstein's formula.
Rewriting E = mc^2
The link below is Einstein speaking and explaining that (E = mc^2) means
mass and energy are (basically) the "same thing". If the important thing
about (E = mc^2) is the proportionality between mass and energy,
then notice that the equation E=mc^2 is written rather oddly. It always
looks to me like an energy equation (sans the 1/2), yet it is really a
linear, proportionality equation. What seems at first glance to be velocity
square term (c^2) term is really the proportionality constant.
The math books
I was taught from always used the format below for a proportional, or straight
line, relationship.
y = ax
where
x is independent variable
y is dependent variable
a is constant of proportionality
To get the E=mc^2 equation in this format all we need
do is reverse the order of the terms on the right side of the equation.
E
= (c^2)m
Curiously, I have never seen E=mc^2 written as
shown above, even though it is the standard format for a proportional relationship.
In this format it is much more obvious, at least to me, that mass scaled
by a huge proportionality constant is equivalent to energy.
http://www.aip.org/history/einstein/voice1.htm
Relativistic mass
There is sometimes
confusion surrounding the subject of mass in relativity. This is
because there are two separate uses of the term. Sometimes people
say "mass" when they mean "relativistic mass", mr but at other times they
say "mass" when they mean 'invariant mass' or 'rest mass', m0. These
two meanings are not the same. The invariant mass of a particle is
independent of its velocity v, whereas relativistic mass increases with
velocity and tends to infinity as the velocity approaches the speed of
light c. They can be defined as follows:
mr = E/c^2
m0 = sqrt(E^2/c^4 - p^2/c^2)
where E is energy, p is momentum and c is the speed of
light in a vacuum. The velocity dependent relation between the two
is
mr = m0 /sqrt(1 - v^2/c^2)
Einstein's
famous equation E=mc^2 remains generally true for all observers only
if the m in the equation is considered to be relativistic mass (mr).
---------------------------------------------
How an increase in kinetic energy of a relativistic
particle increases its mass
Let's think
about the kinetic energy of one of these particles traveling close to the
speed of light. Recall that in an earlier lecture we found the kinetic
energy of an ordinary non-relativistic (i.e. slow moving) mass m was ½mv².
The way we did that was by considering how much work we had to do to raise
it through a certain height - we had to exert a force equal to its weight
W to lift it through height h, the total work done, or energy expended,
being force x distance, Wh. As it fell back down, the force of gravity,
W, did an exactly equal amount of work Wh on the falling object, but this
time the work went into accelerating the object, to give it kinetic energy.
Since we know how fast falling objects pick up speed, we were able to conclude
that the kinetic energy was ½mv².
More generally,
we could have accelerated the mass with any constant force F, and found
the work done by the force (force x distance) to get it to speed v from
a standing start. The kinetic energy of the mass, E = ½mv²,
is exactly equal to the work done by the force in bringing the mass up
to that speed. (It can be shown in a similar way that if a force is applied
to a particle already moving at speed u, say, and it is accelerated to
speed v, the work necessary is ½mv² - ½mu².)
It is interesting to try to repeat the exercise for a
particle moving very close to the speed of light, like the particles in
the accelerators mentioned in the previous paragraph. Newton's Second Law,
in the form
Force = rate of change of momentum
is still true, but close to the speed of light the speed
changes negligibly as the force continues to work -- instead, the mass
increases! Therefore, we can write to an excellent approximation,
Force = (rate of change of mass) x c
where as usual c is the speed of light. To get more specific,
suppose we have a constant force F pushing a particle. At some instant,
the particle has mass M, and speed extremely close to c. One second later,
since the force is continuing to work on the particle, and thus increase
its momentum from Newton's Second Law, the particle will have mass M +
m say, where m is the increase in mass as a result of the work done by
the force.
What is the
increase in the kinetic energy E of the particle during that one second
period? By exact analogy with the non-relativistic case reviewed above,
it is just the work done by the force during that period. Now, since the
mass of the particle changes by m in one second, m is also the rate of
change of mass. Therefore, from Newton's Second Law in the form
Force = (rate of change of mass) x c,
we can write
Force = mc.
The increase in kinetic energy E over the one second period
is just the work done by the force,
force x distance.
Since the particle is moving essentially at the speed
of light, the distance the force acts over in the one-second period is
just c meters (c = 3×10^8 m/sec). So the total work the force does
in that second is
force x distance = mc x c = mc²
Hence the relationship between the increase in mass of
the relativistic particle and its increase in kinetic energy is:
E = mc²
Mass increase is equal to the total work done divided
by c²
At lower speeds
we can show how E=mass x c^2 includes kinetic energy by doing an expansion
of the equation of relativistic mass. Consider a mass M, moving at
speed v, much less than the speed of light. Its kinetic energy is E =½Mv².
Its relativistic mass is M/sqrt(1 - v²/c²), which we can write
as M + m. What is m? For small v/c we can make the following approximatations:
sqrt(1 - v²/c²)
=> (1 - ½v²/c²)
1/(1 - ½v²/c²)
=> (1 + ½v²/c²)
total (relativistic) mass at speed v is
M/sqrt(1 - v²/c²) => M(1 + ½v²/c²)
= M + ½Mv²/c² = M + m
m = ½Mv²/c²
so Einstein's total energy = mass x c^2 becomes
Energy = (M +m)c² = Mc² + ½Mv²
By expanding
the relativistic mass equation we have shown that for low (v/c) the total
energy of a particle is just its rest energy (Mc²), where M = rest
mass, plus its kinetic energy (½Mv²). We conclude
that when a force does work accelerating a body to give it kinetic energy,
the mass of the body increases by an amount equal to the total work done
by the force, the energy transferred, divided by c².
----------------------------------------------------------
Reversible example of E=m x c^2
The helium
atom has a nucleus which has two protons and two neutrons bound together
very tightly by a strong nuclear attraction force. If sufficient outside
force is applied, this can be separated into two "heavy hydrogen" (deuterium)
nuclei, each of which has one proton and one neutron. A lot of outside
energy has to be spent to achieve this separation. It is found that the
total mass of the two heavy hydrogen nuclei is measurably (about half a
percent) heavier than the original helium nucleus.
This extra
mass, multiplied by c², is just equal to the energy needed to split
the helium nucleus in half. Even more important, this energy can
be recovered by letting the two heavy hydrogen nuclei collide and join
to form a helium nucleus again. They are both electrically charged positive,
so they repel each other, and must come together fairly fast to overcome
this repulsion and get to the closeness where the much stronger nuclear
attraction kicks in. This is, of course, fusion, the basic power
source of the hydrogen bomb, and of the sun.
----------------------------------------------------------
Electric forces are huge!
Since positive
and negative charges are almost always in balance, or nearly in balance,
we have little intuition of how huge electric forces really are. The example
below of 1 million tons of repulsion is for the huge distance of 1 meter.
Note that the force goes up inversely with the square of the distance,
so at 1 cm distance the force would be 10^4 higher, or 10 billion tons!
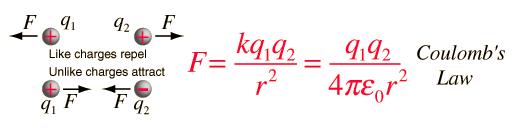
Here's the math. Current is the flow of charge {I = delta
q/delta time}. In the example above the bulb current is 1 amp (1
amp x 120 volt = 120 watt). 1 amp = 1 coulomb/sec, so in the example above
q = 1 coulomb.
F = q^2/4 pi e0 r^2
where
f = newtons
q = coulombs
e0 = electric permitivity of vacuum (8.8 x 10^-12)
r = meters
F = 1/4 pi x 8.8 x 10^-12 x 1
= 1/110 x 10^-12
= 9 x 10^-3 x 10^12
= 9 x 10^9 newtons
To convert newtons to pounds of force think of a 1 Kg
weight sitting on a table. A 1 kg in English units weighs 2.2 lbs. F =
ma and acceleration of gravity on earth is 9.8 m/sec^2 so
F = m x a =1 kg x 9.8 m/sec^2 = 9.8 newtons
so
9.8 newtons <==> 2.2 lbs force
converting
F = 9 x 10^9 newtons x (2.2 lb/9.8 newton) x (1 ton/2,000 lbs)
= 10^6 tons (1 million tons)
----------------------------------------------------------
Lorentz reference 'ether' frame (5/07/09)
Physicist
Hans Ohanian in his excellent new book 'Einstein's Mistakes' says that
Hendrik Lorentz, whom Einstein revered and who had discovered the
Lorentz
transformations before Einstein in his study of electromagnetism, continued
to believe until his death in 1928 that absolute Newtonian time existed.
He believed that time relative to the ether was the absolute Newtonian
time. Clocks moving relative to the ether measured "local time" and were
subject to time dilation. Lorentz had explained in 1895 that Michelson-Morley
experiment had failed to detect motion through the ether because of length
contraction in one arm in the interferometer and time dilation. Einstein,
and most physicist since, have concluded that the null results of experiments
to measure the speed of the ether is best explained by concluding there
is no ether.
Lorentz lived
more than two decades after Einstein's 1905 relativity paper and many years
after it was well accepted. Lorentz agreed with Einstein that observers
in inertial frames saw things equivalently and that they were unable to
sense if they were stationary or moving relative to the ether. Poincare
had written a paper on (special) relativity before Einstein. In fact, in
the early the theory was generally known as Lorentz-Einstein relativity
(sometimes Poincare name was included). Both Lorentz and Poincare continued
to believe in the ether all their lives that frames are
not
relative, they just appear that way to observers moving with a constant
relative velocity. Michelson believed in the ether until his death too.
When I read
about this in Ohanian's book, it gave me an idea. If Lorentz and other
famous physicists continued to believe in the ether as an absolute
reference frame, it must be that recasting relativity problems into
a fixed reference frame does not introduce any mathematical error.
So why not use a 'fixed' reference frame (mythical or not) in working relativity
problems. Seems to be this viewpoint might be useful, and it might very
well be simpler because the speed of light can be drawn as a constant in
this reference frame. (I always find that the lack of a reference frame
to be one of the confusing aspects of working special relativity problems.)
Lorentz's belief
in a reference ether frame (virtually) proves that working with a fixed
ether frame has to be mathematically equivalent to the more conventional
approach. Why not use this fact to get the right answers? As an engineer,
this seems to me to be a sensible thing to do. For years engineers have
successfully used this approach: one example being the use of the 'impulse'
function in circuit analysis. My professors at MIT introducing it said
that it may not be mathematically rigorous, but it was convenient and always
appeared to give the right answer, so it was used extensively in circuit
analysis. (Years later I believe the mathematicians did show it to be rigorous.)
Background microwave radiation -- new preferred
reference frame
Ohanian makes
the point that a with the discovery of the microwave background radiation
there is now a preferred reference frame. In other words everything is
not
relative!
Doppler effects from an ether viewpoint
Below is a
figure I drew showing light pulses traveling in the fixed (Lorentz) ether
frame. Light travels in the ether about 1 nsec/foot (c). Each small box
of the grid is one foot, so the light flashes (black arrow) drift rightward
at c. The light source (black box on left) is assumed flash briefly every
5 nsec. Thus the source creates in the ether a pulse train (series of light
flashes) that drift rightward at c, or 5 box (feet) in 5 nsec.
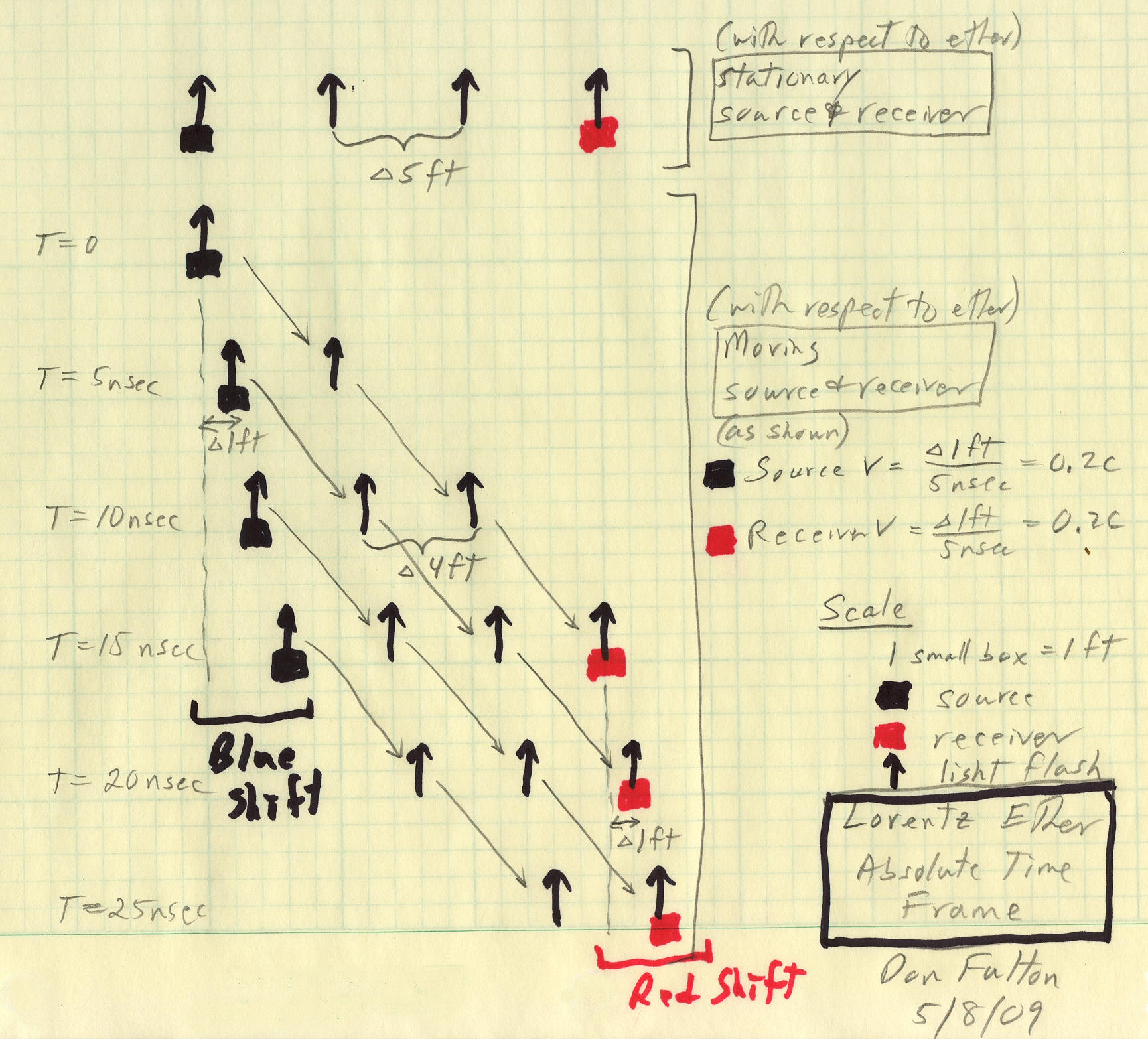
Stationary case
At the top of the
figure the source and receiver (say respectively the back and front of
a space ship) are stationary in the ether. The pulse train in the ether
is a series of light flashes spaced 5 feet (5 box) apart. The receiver
sense a flash every 5 nsec, or exactly at the rate (frequency) as the sources
is sending.
Blue shift at source
In the lower
part of the figure the source and receiver are both moving with respect
to the ether rightward at (a constant speed) 0.2c, or 1 box/5 nsec. The
light flashes in the ether are shown at 5 nsec intervals. Each light flash
upon entering the ether moves at c, drifting rightward at 5 box/5nsec exactly
as in the stationary case. Note, however, the spacing between the light
flashes in the ether has changed. The spacing in the ether is now 4 feet
not 5 feet as in the stationary case.
Why is this?
It's a doppler effect. The source moving in the same direction as
the light (@ 0.2c) somewhat closes the gap to the previous flash. It travels
20% as far as the light, so the spacing of the light flashes in the ether
is compressed from 5 feet to 4 feet. It's a doppler blue shift.
In frequency terms the spacial frequency is higher. (If the source
had been sending sinewaves, then in space the crests would be seen to be
closer together, it's a higher spacial frequency.)
Red shift at receiver
So does the moving
receiver see a higher frequency (equivalently less time between pulses)
that the source is sending? No. Why not. At the receiver there is a doppler
red shift, just the the opposite of what happens at the source. The receiver
is moving away from the incoming light flashes at 0.2c, so even though
the light flashes in the ether are (actually) separated by four feet (equivalent
to 4 nsec), the receiver is running away from the light at 0.2c, so it
'sees' a light flash every 5 nsec, which is exactly at the rate (frequency)
the sources is sending.
The
amplitude of a doppler shift is proportional to the speed of the source
or receiver through the ether. In this case they are both traveling at
the same speed (0.2c). From the perspective of the (fixed absolute)
ether frame in which light travels we see that what is 'really' happening:
The blue doppler shift at the source is exactly cancelled by
the red doppler shift at the receiver, so the receiver 'sees' the
time between flashes to be exactly the same as the source (5 nsec)!
For a receiver
not
moving (with respect to the ether) the pulses are received every 4 nsec,
in other words he sees the pulse rate blue doppler shifted due to
the inward motion of the source.
Gravitational red shift
Well what's so interesting
about that? Well perhaps at constant speed not much, but we can use the
same viewpoint for an accelerating space ship. Now when the light
arrives at the receiver on the front of the ship, sent from a source at
the back of the ship, the receiver is now moving faster (with respect to
the ether) than at the time the source fired the light pulse because the
ship is accelerating. We are now in position to see why light fired
in the direction of the accelerating space ship is (gravitationally) red
shifted.
The
red shift at the faster moving receiver (with respect to the ether) is
larger
than the blue shift at the source. The red and blue shift no longer cancel
leaving a net red shift for light fired in the direction of acceleration.
(For light fired in the direction opposite to acceleration there is a gravitational
blue shift.)
General relativity test
In terms of
the earth this means earth's gravity causes light fired upward to
redden
and light coming into earth downward to shift toward blue.
The gravity on the sun 'surface' is about x28 higher than earth, so Einstein
proposed a test of relativity to measure the frequency of spectral element
lines as seen in the solar spectrum and compare them with the frequency
measured on earth. The sun's spectral lines are expected to be about 2
parts in a million lower in frequency due to the sun's higher gravity over
the earth. This frequency shift (with a lot of complications) has been
verified to tolerance of a few percent.
Clocks slowed by gravity
But the receiver
over time cannot just sense less flashes than are being sent, flashes just
don't get disappear. So there must more to the explanation than just a
doppler shift! Einstein in an early general relativity paper provided the
answer:
The
clocks at the source and receiver run at different rates. Adjusting the
clock at the receiver to run slower will provide more time to count
pulses, and if done right, mirabile dictu the doppler effect is gone. [By
the equivalence principle someone in a sealed box can't determine if the
box is continuously accelerating or sitting on a planet surface in a gravitational
field.] So above explains the gravitational red shift of light and
why clocks in gravitational fields run slower (these are general
relativity effects).
Physical explanation for length contraction
Ohanian says
what bothered many of Einstein's contemporaries was that relativity was
totally mathematical. There was no mechanism proposed, hence no possible
visualization, of how length contraction (or time dilation) worked.
The math just said that for the speed of light to be constant to all observers
the length of moving objects had to (in an unspecified way) contract in
the direction of motion and moving clocks had to run slower. There was
no explanation, zero, of how these effects occurred at a molecular level
or any level.
What's interesting
is that Ohanian says there now is a quantum mechanical explanation
for length contraction (& indirectly I think for time dilation). He
says the calculation could not be done in the early years of relativity
because it requires
relativistic quantum mechanics. This became
available in the form of Dirac's relativistic quantum mechanical equation
in 1928.
Ohanian says
in 1941 W.F.G. Swann calculated that a bar quantum mechanically does contract
while moving, but nobody paid any attention. In 1976 it was again calculated
again by J.S. Bell of CERN and Bell urged this material be put in textbooks
on relativity. Ohanian says no current textbook includes this material
and very few even mention that "length contraction and time dilation have
a physical explanation." The only physical visualization mechanism
found in textbooks is the light clock, but Ohanian criticism is that this
is a very special case, for example, it only works when light bounced perpendicular
to motion. Also the light clock provides no intuition as to how the shape
or size of atom or molecules might change to to speed induced effects of
the their electric fields.
Michelson - Morley Experiment in ether frame (5/09)
The
Michelson - Morley interferometer experiment was strongly featured in my
freshman physics course, but I had long forgotten all the details remembering
only the conclusion: the speed of light was the same in all orientations.
The time to travel out and back in quadrature tubes was compared in various
orientations relative to earth and the earth's motion around the sun and
no variation was found, i.e. the interferometer stayed nulled regardless
of how it was oriented on earth or in space.
19th century viewpoint
* Light moves at a fixed speed (c) relative to the ether
* Ether assumed to be fixed relative to the sun
* Earth in its motion around sun is moving through the ether
(might be some partial entrainment)
* Velocities add and subtract in a newtonian way
* Light travel time goes down traveling with the ether flow,
goes up traveling against the ether flow, and always
the round trip time increases
Animation
Below is a
link to good animation of the Michelson-Morley experiment in the earth's
frame with the ether flowing by. The simulation shows the flow of the ether
(relative to earth) and can be adjusted. This is the world as viewed (before
the experiment) by everyone including Michelson from the earth's frame.
. If you adjust
the speed of the ether in the simulation to up near c, an asymmetry in
travel times is clearly evident. Light traveling in the same direction
as the ether can only (in the limit) be doubled in speed (c + c) = 2c,
but light traveling against the ether can be slowed (in the limit) to a
stop
(c - c) = 0. The result of this asymmetry is that the round trip travel
time is always increased by the flow of the ether. The extra time
it takes traveling against the ether is always (at least a little)
more
than than the time saved traveling with the ether.
http://galileoandeinstein.physics.virginia.edu/more_stuff/flashlets/mmexpt6.htm
The mathematics
for out and back in an 8 foot long tube moving with ether flow at v (relative
to the ether) are as follows:
Time (out & back) = 8 ft/(c+v) + 8ft/(c-v)
= (8ft/c)[1/(1 + v/c) + 1/(1 - v/c)]
= (16 ft/c)[1/(1 - (v/c)^2]
When moving
in the same direction as the ether, the doppler shifts going into and out
of the ether don't quite cancel. There is a residual 2nd order term (v/c)^2
that slightly increases the time it takes for light to go out and
back. The correction factor is 1/ [1 - (v/c)^2]. Note, no square root,
it is not the usual Lorentz correction factor, it's the lorentz
correction factor squared.
Sketch of light flashes out and back from eiher perspective
The increase
in transit time (out and back) is confirmed and can be visualized in a
rough sketch I made in the Lorentz fixed ether frame. Here Earth is speeded
up to 20% of speed of light ( v = 0.2c). The sketch shows that when light
travels with the ether flow spacially it's doppler blue shifted,
the spacing of the light flashes in the ether is 4 boxes. The reflecting
mirror introduces a doppler red shift, so in the reverse direction
the spacial separation of the light flashes in the ether is 6 boxes.
The sketch
shows graphically that round trip time for each light flash is 16.666 nsec,
whereas it with no ether flow it would be 16.0 nsec, so round trip time
is increased about 4% compared to no ether flow. More exactly the increase
in travel time is by the factor 16.6666 nsec/16 nsec = 1.041666 = 1/0.96.
Plugging v= 0.2c into the correction factor above:
[1/(1 - (v/c)^2] = [1/(1- (0.2)^2] = [1/(1 - 0.04)[ = 1/0.96 checks
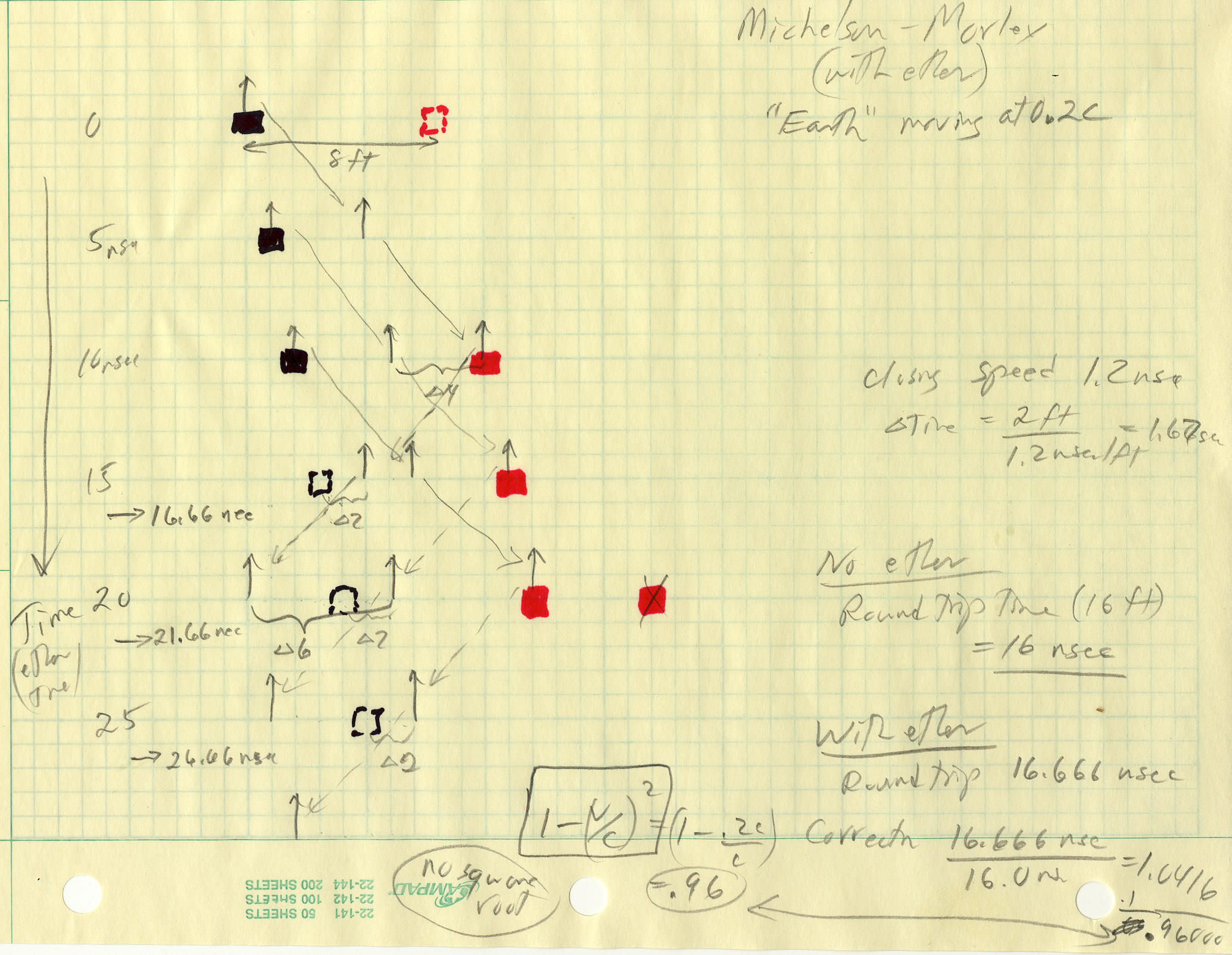
Lorentz explanation
Lorentz, so
I had read, explained the failure of the Michelson Morley experiment by
saying the tube aligned with the ether flow length contracted. This is
the origin of the famous lorentz contraction. But this didn't seem right.
The travel time increase in the tube aligned with the ether flow is 1/(1
- (v/c)^2), it's only partially corrected by a length correction of sqrt{1
- (v/c)^2}.
For a while
I thought the answer must be that Lorentz in 1895 had proposed a length
contraction
and a time dilation (slowing of the clock). With two
lorentz corrction factors at work the effects of ether flow in the aligned
tube [1/(1 - (v/c)^2)] would be cancelled. But I had missed something.
A null Michelson Morley result just means the travel times in the two
90 degree tubes are the same.What I had missed is that the ether
flow changes (increases) the round trip travel times in both tubes.
The 90 degree tube is effectively a light clock! It's 'beating'
is slowed (dilated) by travelling (in the ether) meaning it takes longer
(by a lorentz correction factor) for the light to make a round trip.
90 degree tube is a light clock!
Seen from
the fixed ether frame the light flash in the 90 degree tube on the moving
earth is traveling not only out and back but also forward with the earth.
The light path (seen by an outside observer in the fixed either (sun) frame)
is two diagonals whose base is (v x delta t). Thus with ether flow the
round trip time in the 90 degree tube is increased by 1/sqrt{1 - (v/c)^2}.
This is about half the [1/(1 - (v/c)^2)] increase in the tube aligned with
the ether flow. Hence a lorentz length contraction [sqrt{1 - (v/c)^2}]
of only the tube aligned with the ether flow does the trick. It
cuts the extra travel time of the aligned tube (about) in half matching
the travel time in the quadrature tube. The equations of Michelson Morley
showing all this are here:
http://www.relativitycalculator.com/Albert_Michelson_Part_II.shtml
Bottom line on Michelson Morley
* From an
earth perspective there is no motion so length contraction (or time dilation).
The null result of the experiment is proof light is not being conducted
in an ether flowing through earth.
* From an outsider
in the fixed ether frame (here assumed to be attached to the sun) the earth
is moving.
The
arm not aligned with the earth's travel around the sun acts like
a light clock. It's light not only has to go out and back but also move
perpendicularly through space, hence the round trip time in that arm is
increased
by
the lorentz factor (1/sqrt{1 - (v/c)^2}).
The arm aligned
with
the earth's motion around the sun has an increased in round trip time due
to the doppler blue and red shifts going into and out of the ether that
don't quite cancel. This results in an increase in round trip travel time
of [1/(1 - (v/c)^2)], which is roughly two lorentz factors. However, this
arm pointed in the direction of motion is length contracted, which reduces
travel time by a lorentz factor. The combined result of these two terms
in an increase in round trip time by the lorentz factor (1/sqrt{1 - (v/c)^2}).
The increase
in round trip time due to earth's motion is thus the same both arms which
explains why the interferometer stays balanced with no fringe changes.
------------
Wikipedia
says this about the length contraction in the Michelson Morley experiment
article (5/14/09)
The
explanation (for the null result) was found in the Fitzgerald–Lorentz contraction.
According to this physical law all objects physically contract along
the line of motion (originally thought to be relative to the ether),
so while the light may indeed transit slower on that arm, it also ends
up travelling a shorter distance that exactly cancels out the drift.
It's poorly worded
('cancels out the drift'). Also I sees there are different opinions as
whether an object 'physically' length contracts, or whether it just appears
to contract by an outside observer who is not moving. I generally tend
toward toward the latter view. But in the Michelson Morley experiment it
certainly seems that saying it physically contracts is right, because the
human observer sees no fringe changes.
Contraction due to earth's speed around sun
The earth's
speed around the sun is about 30 km/sec (3 x 10^4 m/sec), so (v/c)^2 =
[(3 x 10^4/(3 x 10^8)]^2 = 10^-8. So the expected increase in round trip
travel time in the arm aligned with the ether was about 1 part in 100 million,
and in the quadrature tube about half this (1/2 part in 100 million). If
the aligned tube length contracts, then it causes the the round trip times
in both tubes to be the same (up about 1/2 part in 100 million from the
case of no ether flow).






